湘教版七年级上册数学期中试题2(含解析)
文档属性
| 名称 | 湘教版七年级上册数学期中试题2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 866.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 08:07:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版七年级上册数学期中试卷
一、选择题。(每小题只有一个答案正确)
1.如果温度上升10℃记作+10℃,那么温度下降5℃记作( )
A.+10℃ B.﹣10℃ C.+5℃ D.﹣5℃
2.的相反数是( )
A.2017 B. C. D.-2017
3.下列说法正确的是( )
A.a一定是负数 B.a的绝对值等于a
C.正数、负数和0统称为有理数 D.整数、分数统称为有理数
4.我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000,这个数用科学记数法表示为( )
A. B. C. D.
5.多项式的次数及最高次项的系数分别是( )
A.3,-3 B.2,-3 C.5,-3 D.3,1
6.下列各式中,正确的是( )
A.3a+3a=6a2 B.3a﹣a=3 C.2a3+3a2=5a5 D.-3a2b+2a2b=-a2b
7.下列方程变形正确的是( )
A.方程化成
B.方程,去括号,得 3x25x1
C.方程 移项得
D.方程,未知数系数化为1,得 t=1
8.有理数a、b在数轴上的位置如图所示,则化简|a﹣b|-b的结果为( )
A.a B.-a C.-a-2b D.a-2b
9.如图,阴影部分的面积是( )
A.xy B.xy C.5xy D.2xy
10.已知是两位数,是一位数,把接写在的后面,就成为一个三位数.这个三位数可表示成( )
A. B. C. D.
二、填空题
11.某商店上月收入为a元,本月收入比上月的2倍还多10元,本月的收入是______元.
12.若与是同类项,则+_____.
13.a、b互为倒数,x、y互为相反数,|m|=2且m<0,则______.
14.若是关于x的一元一次方程,则m的值是_______.
15.如果多项式-2a+3b的值为5,则多项式9b-6a+2的值等于_______.
16.下列图案是用长度相同的小木棒按一定规律拼搭而成,图案①需8根小木棒,图案②需15根小木棒,……,按此规律,第n个图案需要的小木棒的根数是__________.(用含n的式子表示)
三、解答题
17.计算
(1);
(2).
18.解方程
(1);
(2).
19.在数轴上表示下列各数,并用“<”把这些数连接起来:1,-1,0,|-4|.
20.先化简,再求值,其中.
21.已知,,且的值与无关,求的值.
22.一位同学做一道题:已知两个多项式A、B,计算“3A+B”.他误将“3A+B”看成“A+3B”,求得的结果为“8x2+x-9”.已知B=x2﹣3,请求出正确的答案.
23.出租车司机小刘某天下午的营运全是在东西走向的大道上.如果规定向东为正,向西为负.他这天下午行车情况如下(单位:千米)
+5,﹣3,﹣8,﹣6,+10,﹣6,+11,﹣9
(1)将最后一名乘客送到目的地时,小刘在下午出车地点A的东面还是西面?离点A的距离是多少千米?
(2)在下午营运开始前出租车油箱内有(58a﹣a2﹣1)升汽油,汽车耗油量a升/千米,问:小刘这个下午从营运开始到送完最后一位乘客,途中是否需要加油?
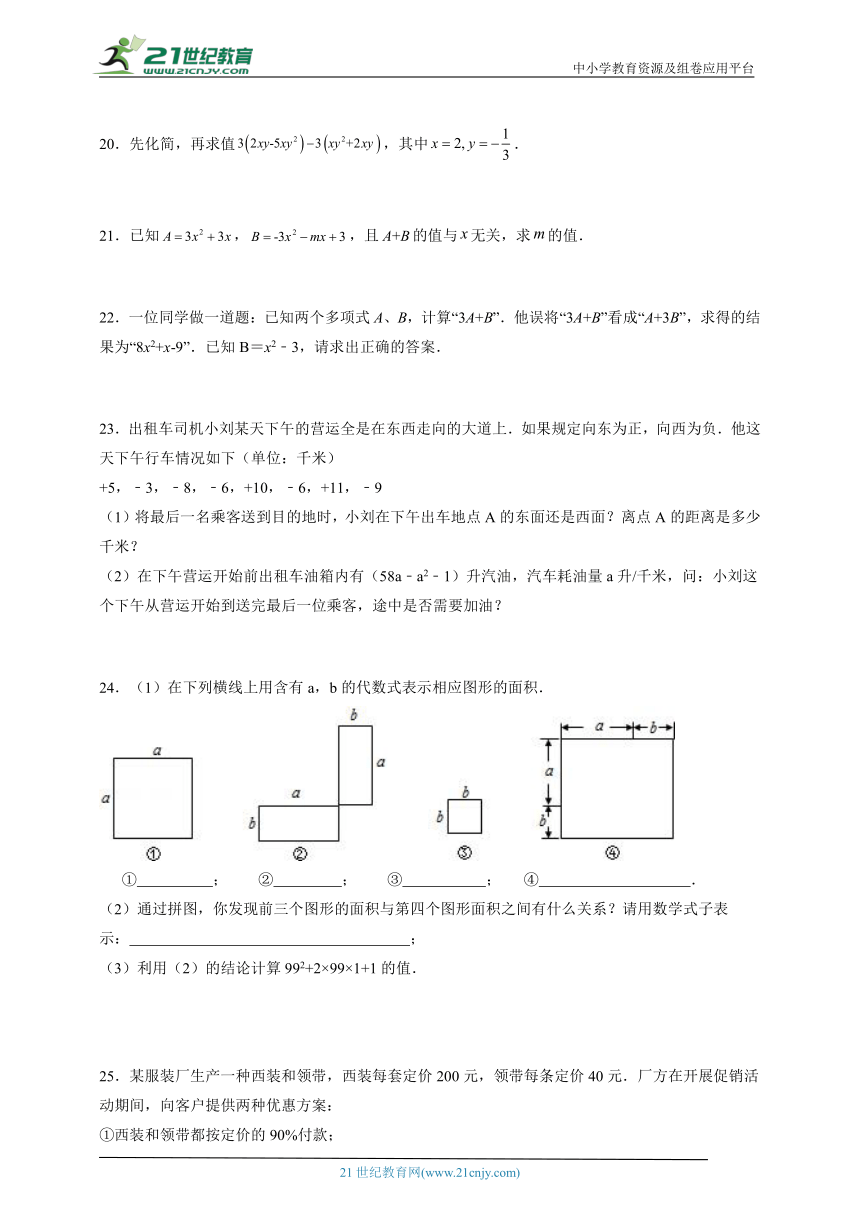
24.(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
① ; ② ; ③ ; ④ .
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算992+2×99×1+1的值.
25.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
①西装和领带都按定价的90%付款;
②买一套西装送一条领带.
现某客户要到该服装厂购买x套西装(x≥1),领带条数是西装套数的4倍多5.
(1)若该客户按方案①购买,需付款______元:(用含x的代数式表示)
若该客户按方案②购买,需付款______元;(用含x的代数式表示)
(2)若x=10,通过计算说明此时按哪种方案购买较为合算?
参考答案
1.D
【分析】
根据用正负数表示具有相反意义的量进行求解即可得.
【详解】如果温度上升10℃记作+10℃,
那么下降5℃记作﹣5℃,
故选D.
【点睛】本题考查了用正负数表示具有相反意义的量,熟练掌握相关知识是解题的关键.
2.D
【分析】
根据绝对值与相反数的定义即可求解.
【详解】
=2017,
∴相反数是-2017
故选D.
【点睛】
此题主要考查相反数的求解,解题的关键是熟知有理数的性质.
3.D
【分析】
根据正、负数、绝对值及有理数的概念进行判断,即可得出结论.
【详解】
A、当a是负数时,a是正数,则a不一定是负数,故此选项说法错误,不符合题意;
B、当a是正数时,a的绝对值等于a,故此选项说法错误,不符合题意;
C、正有理数、负有理数和0统称为有理数,故此选项说法错误,不符合题意;
D、整数、分数统称为有理数,故此选项说法正确,符合题意.
故选:D.
【点睛】
本题考查了有理数的相关概念,熟练掌握正、负数、绝对值及有理数的概念是解题的关键.
4.C
【分析】
科学记数法的表示较大的数形式为a×10n的形式,其中1≤|a|<10,n为整数.其中a是整数数位只有一位的数,10的指数n比原来的整数位数少1.
【详解】
解:4 400 000 000=4.4×109,
故选:C.
【点睛】
此题主要考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.
5.A
【分析】
根据多项式中次数最高的项的次数叫做多项式的次数可得此多项式为3次,最高次项是-3xy2,系数是数字因数,故为-3.
【详解】
多项式1+2xy-3xy2的次数是3, 最高次项是-3xy2,系数是-3;
故选A.
【点睛】
此题主要考查了多项式的次数与系数,关键是掌握多项式次数的计算方法与单项式的区别.
6.D
【分析】
根据整式的加减运算法则即可判断.
【详解】
A.3a+3a=6a,故错误;
B.3a﹣a=2a,故错误;
C.2a3+3a2不能合并,故错误;
D.-3a2b+2a2b=-a2b,正确
故选D.
【点睛】
此题主要考查整式的加减,解题的关键是熟知其运算法则.
7.C
【分析】
根据一元一次方程的解法分别进行计算,即可得出结论.
【详解】
解:A、方程化成;故此选项变形错误,不符合题意;
B、方程,去括号,得;故此选项变形错误,不符合题意;
C、方程,移项得;故此选项变形正确,符合题意;
D、方程,未知数系数化为1,得;故此选项变形错误,不符合题意.
故选:C.
【点睛】
此题考查了解一元一次方程,掌握解一元一次方程的一般步骤及方法是解题的关键.
8.B
【分析】
根据数轴的特点得到a﹣b<0,再根据去绝对值的方法即可求解.
【详解】
由熟知可得a<0,b>0,a﹣b<0,
∴|a﹣b|-b=b-a-b=- a
故选B.
【点睛】
此题主要考查去绝对值,解题的关键是熟知数轴的特点及取绝对值的方法.
9.A
【详解】
试题分析:根据图形特征结合三角形、长方形、正方形的面积公式求解即可.
由图可得阴影部分的面积
故选A.
考点:阴影部分的面积
点评:求阴影部分的面积是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.
10.C
【解析】两位数的表示方法:十位数字×10个位数字;三位数的表示方法:百位数字×100十位数字×10个位数字.是两位数,是一位数,依据题意可得扩大了100倍,所以这个三位数可表示成.
11.(2a+10)
【分析】
由已知,本月的收入比上月的2倍即2a,还多10元即再加上10元,就是本月的收入.
【详解】
根据题意得: 本月的收入为:(2a+10)元.
故答案为(2a+10).
【点睛】
此题考查了学生根据意义列代数式的掌握,关键是分析理解题意.
12.10
【分析】
根据同类项是字母相同,且相同字母的指数也相同,可得m、n的值,再根据有理数的加法,可得答案.
【详解】
解:与是同类项
m-2=5,n+1=4,
m=7,n=3,
m+n=7+3=10,
故答案为10.
【点睛】
本题考查了同类项,同类项字母相同,且相同字母的指数也相同.
13.4
【分析】
利用相反数,倒数,以及绝对值的代数意义求出各自的值,代入原式计算即可求出值.
【详解】
根据题意得:ab=1,x+y=0,m=2或 2,
∵m<0,
∴m= 2
原式=2+0+2=4,
故答案为4.
【点睛】
此题考查了有理数的混合运算,求代数式的值,熟练掌握运算法则是解本题的关键.
14.-1
【分析】
根据一元一次方程的定义确定m的值.
【详解】
解:∵是关于x的一元一次方程
∴且
解得:m=-1
故答案为:-1.
【点睛】
本题考查一元一次方程的定义,正确理解并掌握概念是解题关键.
15.-13
【分析】
根据-2a+3b=5,整体代入即可求解.
【详解】
∵-2a+3b=5,
∴9b-6a+2=-3(-2a+3b)+2=-15+2=-13
故答案为:-13.
【点睛】
此题主要考查代数式求值,解题的关键是熟知整体代入法的运用.
16.
【分析】
先观察图案得出前3个图案需要的小木棒的根数,再归纳类推出一般规律即可得.
【详解】
观察图案可知,第1个图案需要的小木棒的根数是,
第2个图案需要的小木棒的根数是,
第3个图案需要的小木棒的根数是,
归纳类推得:第n个图案需要的小木棒的根数是,
故答案为:.
【点睛】
本题考查了列代数式表示图形的规律,观察图案,正确发现规律是解题关键.
17.(1)1;(2)-4.
【分析】
(1)利用有理数加减混合运算的计算方法计算即可;
(2)利用乘法分配律进行简便运算,计算后即可得出结果.
【详解】
解:(1)
;
(2)
.
【点睛】
此题考查了有理数的混合运算,掌握有理数混合运算的运算顺序及相关运算法则是解题的关键.
18.(1)x=(2)x=-23.
【分析】
(1)移项合并,未知数系数化为1即可求解;
(2)去分母,去括号,移项合并,未知数系数化为1即可求解.
【详解】
(1)
3x=1
x=
(2)
3(x-5)-2(2x+1)=6
3x-15-4x-2=6
-x=23
x=-23.
【点睛】
此题主要考查解一元一次方程,解题的关键是熟知解方程的方法.
19.数轴见详解,-1<0<1<|-4|.
【分析】
先画出数轴表示各数,然后根据数轴左边的数小于右边的数解答即可.
【详解】
解:如图所示:
∴-1<0<1<|-4|.
【点睛】
本题主要考查了利用数轴比较有理数的大小,熟练掌握数轴是解题的关键.
20.;-4.
【分析】
先根据整式的加减运算法则化简,再代入x,y即可求解.
【详解】
=
=
把代入原式==-4.
【点睛】
此题主要考查整式的化简求值,解题的关键是熟知整式的加减运算法则.
21.3
【分析】
先合并,再根据值与无关,求出的值.
【详解】
==(3-m)x+3
∵值与无关,
∴3-m=0,解得m=3.
【点睛】
此题主要考查整式加减运算的应用,解题的关键是熟知整式的加减运算法则.
22.-5x2-21
【分析】
设A=ax2+bx+c,然后将A、B代入A+3B=8x2+x-9,确定多项式A,最后计算3A+B即可.
【详解】
解:设A=ax2+bx+c,
∵A+3B=8x2+x-9
∴ax2+bx+c+3(x2﹣3)= x2﹣3,即(a+3)x2+bx+(c-9)= 8x2+x-9
∴a+3=8,b=1,c-9=-9,即,a=5,b=1,c=0
∴A=5x2+x,
∴3A+B
=3(5x2+x)+ x2﹣3
=(15+1)x2+3x-3
=-16x2+3x-3.
【点睛】
本题主要考查了整式的加减,确定多项式A是解答本题的关键.
23.(1)在出发点的A西面,离A的距离是6 千米;(2)需要加油.
【分析】
求出这些数据的和即可判断;
求出这些数据的绝对值的和,列出代数式即可解决问题;
【详解】
解:(1)(千米),
所以小刘在出发点的A西面,离A的距离是6 千米.
(2)(千米),
,
所以需要加油.
【点睛】
本题考查的知识点是正数和负数,解题关键是注意不论正数还是负数,都耗油,计算路程耗油时要加绝对值.
24.(1)①a2;②2ab;③b2;④(a+b)2;(2)a2+2ab+b2=(a+b)2;(3)10000.
【详解】
试题分析:(1)根据图形可以求得各个图形的面积;
(2)通过观察可以得到前三个图形的面积与第四个图形面积之间的关系,从而可以用式子进行表示;
(3)根据问题(2)发现的结论可以得到992+2×99×1+1的值.
试题解析:
(1)由图可得,
图①的面积是:;图②的面积是:ab+ab=2ab;图③的面积是:;图④的面积是:
故答案为①;②2ab;③;④
(2)通过拼图,前三个图形的面积与第四个图形面积之间的关系是前三个图形的面积之和等于第四个图形的面积,用数学式子表示是:
25.(1)324x+180(元),320x+200(元);(2)所以方案二合算.
【详解】
试题分析:(1)仔细认真阅读题中的数量关系,首先要明白领带和西装的数量关系.其次要明白商家的活动方案,根据方案计算.
①需付款为:领带价钱的90%+西装价钱的90%.
②需付款为:(领带条数﹣x)条领带价钱+西装价钱.
(2)把x=10代入(1)中的两个式子即可.
解:(1)∵现某客户要到该服装厂购买x套西装(x≥1),领带条数是西装套数的4倍多5.
∴领带条数是4x+5.
若该客户按方案①购买,则200x×90%+40(4x+5)×90%=324x+180(元).
若该客户按方案②购买,则200x+40×(4x+5﹣x)=320x+200(元);
(2)若x=10,该客户按方案①购买,则324x+180=3420(元).
该客户按方案②购买,则320x+200=3400(元).
3420>3400
所以方案二合算.
考点:代数式求值;列代数式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版七年级上册数学期中试卷
一、选择题。(每小题只有一个答案正确)
1.如果温度上升10℃记作+10℃,那么温度下降5℃记作( )
A.+10℃ B.﹣10℃ C.+5℃ D.﹣5℃
2.的相反数是( )
A.2017 B. C. D.-2017
3.下列说法正确的是( )
A.a一定是负数 B.a的绝对值等于a
C.正数、负数和0统称为有理数 D.整数、分数统称为有理数
4.我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000,这个数用科学记数法表示为( )
A. B. C. D.
5.多项式的次数及最高次项的系数分别是( )
A.3,-3 B.2,-3 C.5,-3 D.3,1
6.下列各式中,正确的是( )
A.3a+3a=6a2 B.3a﹣a=3 C.2a3+3a2=5a5 D.-3a2b+2a2b=-a2b
7.下列方程变形正确的是( )
A.方程化成
B.方程,去括号,得 3x25x1
C.方程 移项得
D.方程,未知数系数化为1,得 t=1
8.有理数a、b在数轴上的位置如图所示,则化简|a﹣b|-b的结果为( )
A.a B.-a C.-a-2b D.a-2b
9.如图,阴影部分的面积是( )
A.xy B.xy C.5xy D.2xy
10.已知是两位数,是一位数,把接写在的后面,就成为一个三位数.这个三位数可表示成( )
A. B. C. D.
二、填空题
11.某商店上月收入为a元,本月收入比上月的2倍还多10元,本月的收入是______元.
12.若与是同类项,则+_____.
13.a、b互为倒数,x、y互为相反数,|m|=2且m<0,则______.
14.若是关于x的一元一次方程,则m的值是_______.
15.如果多项式-2a+3b的值为5,则多项式9b-6a+2的值等于_______.
16.下列图案是用长度相同的小木棒按一定规律拼搭而成,图案①需8根小木棒,图案②需15根小木棒,……,按此规律,第n个图案需要的小木棒的根数是__________.(用含n的式子表示)
三、解答题
17.计算
(1);
(2).
18.解方程
(1);
(2).
19.在数轴上表示下列各数,并用“<”把这些数连接起来:1,-1,0,|-4|.
20.先化简,再求值,其中.
21.已知,,且的值与无关,求的值.
22.一位同学做一道题:已知两个多项式A、B,计算“3A+B”.他误将“3A+B”看成“A+3B”,求得的结果为“8x2+x-9”.已知B=x2﹣3,请求出正确的答案.
23.出租车司机小刘某天下午的营运全是在东西走向的大道上.如果规定向东为正,向西为负.他这天下午行车情况如下(单位:千米)
+5,﹣3,﹣8,﹣6,+10,﹣6,+11,﹣9
(1)将最后一名乘客送到目的地时,小刘在下午出车地点A的东面还是西面?离点A的距离是多少千米?
(2)在下午营运开始前出租车油箱内有(58a﹣a2﹣1)升汽油,汽车耗油量a升/千米,问:小刘这个下午从营运开始到送完最后一位乘客,途中是否需要加油?
24.(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
① ; ② ; ③ ; ④ .
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示: ;
(3)利用(2)的结论计算992+2×99×1+1的值.
25.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
①西装和领带都按定价的90%付款;
②买一套西装送一条领带.
现某客户要到该服装厂购买x套西装(x≥1),领带条数是西装套数的4倍多5.
(1)若该客户按方案①购买,需付款______元:(用含x的代数式表示)
若该客户按方案②购买,需付款______元;(用含x的代数式表示)
(2)若x=10,通过计算说明此时按哪种方案购买较为合算?
参考答案
1.D
【分析】
根据用正负数表示具有相反意义的量进行求解即可得.
【详解】如果温度上升10℃记作+10℃,
那么下降5℃记作﹣5℃,
故选D.
【点睛】本题考查了用正负数表示具有相反意义的量,熟练掌握相关知识是解题的关键.
2.D
【分析】
根据绝对值与相反数的定义即可求解.
【详解】
=2017,
∴相反数是-2017
故选D.
【点睛】
此题主要考查相反数的求解,解题的关键是熟知有理数的性质.
3.D
【分析】
根据正、负数、绝对值及有理数的概念进行判断,即可得出结论.
【详解】
A、当a是负数时,a是正数,则a不一定是负数,故此选项说法错误,不符合题意;
B、当a是正数时,a的绝对值等于a,故此选项说法错误,不符合题意;
C、正有理数、负有理数和0统称为有理数,故此选项说法错误,不符合题意;
D、整数、分数统称为有理数,故此选项说法正确,符合题意.
故选:D.
【点睛】
本题考查了有理数的相关概念,熟练掌握正、负数、绝对值及有理数的概念是解题的关键.
4.C
【分析】
科学记数法的表示较大的数形式为a×10n的形式,其中1≤|a|<10,n为整数.其中a是整数数位只有一位的数,10的指数n比原来的整数位数少1.
【详解】
解:4 400 000 000=4.4×109,
故选:C.
【点睛】
此题主要考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.
5.A
【分析】
根据多项式中次数最高的项的次数叫做多项式的次数可得此多项式为3次,最高次项是-3xy2,系数是数字因数,故为-3.
【详解】
多项式1+2xy-3xy2的次数是3, 最高次项是-3xy2,系数是-3;
故选A.
【点睛】
此题主要考查了多项式的次数与系数,关键是掌握多项式次数的计算方法与单项式的区别.
6.D
【分析】
根据整式的加减运算法则即可判断.
【详解】
A.3a+3a=6a,故错误;
B.3a﹣a=2a,故错误;
C.2a3+3a2不能合并,故错误;
D.-3a2b+2a2b=-a2b,正确
故选D.
【点睛】
此题主要考查整式的加减,解题的关键是熟知其运算法则.
7.C
【分析】
根据一元一次方程的解法分别进行计算,即可得出结论.
【详解】
解:A、方程化成;故此选项变形错误,不符合题意;
B、方程,去括号,得;故此选项变形错误,不符合题意;
C、方程,移项得;故此选项变形正确,符合题意;
D、方程,未知数系数化为1,得;故此选项变形错误,不符合题意.
故选:C.
【点睛】
此题考查了解一元一次方程,掌握解一元一次方程的一般步骤及方法是解题的关键.
8.B
【分析】
根据数轴的特点得到a﹣b<0,再根据去绝对值的方法即可求解.
【详解】
由熟知可得a<0,b>0,a﹣b<0,
∴|a﹣b|-b=b-a-b=- a
故选B.
【点睛】
此题主要考查去绝对值,解题的关键是熟知数轴的特点及取绝对值的方法.
9.A
【详解】
试题分析:根据图形特征结合三角形、长方形、正方形的面积公式求解即可.
由图可得阴影部分的面积
故选A.
考点:阴影部分的面积
点评:求阴影部分的面积是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.
10.C
【解析】两位数的表示方法:十位数字×10个位数字;三位数的表示方法:百位数字×100十位数字×10个位数字.是两位数,是一位数,依据题意可得扩大了100倍,所以这个三位数可表示成.
11.(2a+10)
【分析】
由已知,本月的收入比上月的2倍即2a,还多10元即再加上10元,就是本月的收入.
【详解】
根据题意得: 本月的收入为:(2a+10)元.
故答案为(2a+10).
【点睛】
此题考查了学生根据意义列代数式的掌握,关键是分析理解题意.
12.10
【分析】
根据同类项是字母相同,且相同字母的指数也相同,可得m、n的值,再根据有理数的加法,可得答案.
【详解】
解:与是同类项
m-2=5,n+1=4,
m=7,n=3,
m+n=7+3=10,
故答案为10.
【点睛】
本题考查了同类项,同类项字母相同,且相同字母的指数也相同.
13.4
【分析】
利用相反数,倒数,以及绝对值的代数意义求出各自的值,代入原式计算即可求出值.
【详解】
根据题意得:ab=1,x+y=0,m=2或 2,
∵m<0,
∴m= 2
原式=2+0+2=4,
故答案为4.
【点睛】
此题考查了有理数的混合运算,求代数式的值,熟练掌握运算法则是解本题的关键.
14.-1
【分析】
根据一元一次方程的定义确定m的值.
【详解】
解:∵是关于x的一元一次方程
∴且
解得:m=-1
故答案为:-1.
【点睛】
本题考查一元一次方程的定义,正确理解并掌握概念是解题关键.
15.-13
【分析】
根据-2a+3b=5,整体代入即可求解.
【详解】
∵-2a+3b=5,
∴9b-6a+2=-3(-2a+3b)+2=-15+2=-13
故答案为:-13.
【点睛】
此题主要考查代数式求值,解题的关键是熟知整体代入法的运用.
16.
【分析】
先观察图案得出前3个图案需要的小木棒的根数,再归纳类推出一般规律即可得.
【详解】
观察图案可知,第1个图案需要的小木棒的根数是,
第2个图案需要的小木棒的根数是,
第3个图案需要的小木棒的根数是,
归纳类推得:第n个图案需要的小木棒的根数是,
故答案为:.
【点睛】
本题考查了列代数式表示图形的规律,观察图案,正确发现规律是解题关键.
17.(1)1;(2)-4.
【分析】
(1)利用有理数加减混合运算的计算方法计算即可;
(2)利用乘法分配律进行简便运算,计算后即可得出结果.
【详解】
解:(1)
;
(2)
.
【点睛】
此题考查了有理数的混合运算,掌握有理数混合运算的运算顺序及相关运算法则是解题的关键.
18.(1)x=(2)x=-23.
【分析】
(1)移项合并,未知数系数化为1即可求解;
(2)去分母,去括号,移项合并,未知数系数化为1即可求解.
【详解】
(1)
3x=1
x=
(2)
3(x-5)-2(2x+1)=6
3x-15-4x-2=6
-x=23
x=-23.
【点睛】
此题主要考查解一元一次方程,解题的关键是熟知解方程的方法.
19.数轴见详解,-1<0<1<|-4|.
【分析】
先画出数轴表示各数,然后根据数轴左边的数小于右边的数解答即可.
【详解】
解:如图所示:
∴-1<0<1<|-4|.
【点睛】
本题主要考查了利用数轴比较有理数的大小,熟练掌握数轴是解题的关键.
20.;-4.
【分析】
先根据整式的加减运算法则化简,再代入x,y即可求解.
【详解】
=
=
把代入原式==-4.
【点睛】
此题主要考查整式的化简求值,解题的关键是熟知整式的加减运算法则.
21.3
【分析】
先合并,再根据值与无关,求出的值.
【详解】
==(3-m)x+3
∵值与无关,
∴3-m=0,解得m=3.
【点睛】
此题主要考查整式加减运算的应用,解题的关键是熟知整式的加减运算法则.
22.-5x2-21
【分析】
设A=ax2+bx+c,然后将A、B代入A+3B=8x2+x-9,确定多项式A,最后计算3A+B即可.
【详解】
解:设A=ax2+bx+c,
∵A+3B=8x2+x-9
∴ax2+bx+c+3(x2﹣3)= x2﹣3,即(a+3)x2+bx+(c-9)= 8x2+x-9
∴a+3=8,b=1,c-9=-9,即,a=5,b=1,c=0
∴A=5x2+x,
∴3A+B
=3(5x2+x)+ x2﹣3
=(15+1)x2+3x-3
=-16x2+3x-3.
【点睛】
本题主要考查了整式的加减,确定多项式A是解答本题的关键.
23.(1)在出发点的A西面,离A的距离是6 千米;(2)需要加油.
【分析】
求出这些数据的和即可判断;
求出这些数据的绝对值的和,列出代数式即可解决问题;
【详解】
解:(1)(千米),
所以小刘在出发点的A西面,离A的距离是6 千米.
(2)(千米),
,
所以需要加油.
【点睛】
本题考查的知识点是正数和负数,解题关键是注意不论正数还是负数,都耗油,计算路程耗油时要加绝对值.
24.(1)①a2;②2ab;③b2;④(a+b)2;(2)a2+2ab+b2=(a+b)2;(3)10000.
【详解】
试题分析:(1)根据图形可以求得各个图形的面积;
(2)通过观察可以得到前三个图形的面积与第四个图形面积之间的关系,从而可以用式子进行表示;
(3)根据问题(2)发现的结论可以得到992+2×99×1+1的值.
试题解析:
(1)由图可得,
图①的面积是:;图②的面积是:ab+ab=2ab;图③的面积是:;图④的面积是:
故答案为①;②2ab;③;④
(2)通过拼图,前三个图形的面积与第四个图形面积之间的关系是前三个图形的面积之和等于第四个图形的面积,用数学式子表示是:
25.(1)324x+180(元),320x+200(元);(2)所以方案二合算.
【详解】
试题分析:(1)仔细认真阅读题中的数量关系,首先要明白领带和西装的数量关系.其次要明白商家的活动方案,根据方案计算.
①需付款为:领带价钱的90%+西装价钱的90%.
②需付款为:(领带条数﹣x)条领带价钱+西装价钱.
(2)把x=10代入(1)中的两个式子即可.
解:(1)∵现某客户要到该服装厂购买x套西装(x≥1),领带条数是西装套数的4倍多5.
∴领带条数是4x+5.
若该客户按方案①购买,则200x×90%+40(4x+5)×90%=324x+180(元).
若该客户按方案②购买,则200x+40×(4x+5﹣x)=320x+200(元);
(2)若x=10,该客户按方案①购买,则324x+180=3420(元).
该客户按方案②购买,则320x+200=3400(元).
3420>3400
所以方案二合算.
考点:代数式求值;列代数式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
