12.2一次函数同步练习(含解析)沪科版八年级数学上册
文档属性
| 名称 | 12.2一次函数同步练习(含解析)沪科版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 612.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 22:36:35 | ||
图片预览




文档简介
12.2 一次函数
(考试时间:120分钟 满分:150分)
一.选择题(本大题共10小题,每小题4分,满分40分)
1.下列函数:①;②;③;④,其中一次函数的个数是( )
A.1 B.2 C.3 D.4
2.函数y=-3x-3不经过第( )象限
A.一 B.二 C.三 D.四
3.将直线y=2x向右平移1个单位,再向上平移1个单位后,所得直线的表达式为( )
A.y=2x-1 B.y=2x C.y=2x+4 D.y=2x-2
4.函数值y随x的增大而减小的是( )
A.y=1+x B.y=x﹣1 C.y=﹣x+1 D.y=﹣2+3x
5.已知、是直线上的点,则a、b的大小关系为( )
A. B. C. D.a,b关系不确定
6.若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )
A.-48 D.-4≤b≤8
7.若点(m,n)在函数y=2x+1的图象上,则代数式4m﹣2n+1的值是( )
A.1 B.﹣1 C.2 D.﹣2
8.已知点,,都在直线上,则,,的值的大小关系是( ).
A. B. C. D.
9.一次函数的图像经过点和点,当时,则的取值范围( )
A. B. C. D.
10.在直角坐标平面内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当时, B.当时, C.当时, D.当时,
二.填空题(共4小题,每小题5分,满分20分)
11.直线y=2x-6与y轴的交点坐标为________.
12.若将直线y=﹣2x向上平移3个单位后得到直线AB,那么直线AB的解析式是_____.
13.直线经过点和,则这条直线的表达式为___________.
14.若函数y=(m﹣1)x|m|是正比例函数,则该函数的图象经过第_____________象限.
三.(本大题共2小题,每小题8分,共16分)
15.作出函数的图像,并根据图像回答下列问题:
(1)y的值随x的增大而 ;
(2)图像与x轴的交点坐标是 ;与y轴的交点坐标是 ;
(3)当x 时,y≥0.
16.已知直线y=(5-3m)x+m-4与直线y=0.5x+6平行,求此直线的解析式.
四.(本大题共2小题,每小题8分,共16分)
17.一次函数的图象经过点(-3,-2).
(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
18.已知,且与x成正比例,与成正比例,当时,,当时,
(1)求出y与x之间的函数关系式;
(2)计算时,y的值.
五.(本大题共2小题,每小题10分,共20分)
19.已知是关于的一次函数,且当时,;当时,.
(1)求该一次函数的表达式;
(2)当时,求自变量的值.
20.已知函数,其自变量的取值范围是.当时,;当时,.
(1)根据给定的条件,求出的函数解析式;
(2)根据你所求的函数解析式,选取适当的自变量完成如表,并在下面的平面直角坐标系中描点并画出函数的大致图象:
(3)请画出的图象,并结合图象直接写出:当时,的取值范围是 .
六.(本题满分12分)
21.如图,在平面直角坐标系中,点E的坐标为(4,0),点F的坐标为(0,2),直线11经过点E和点F,直线l1与直线l2:y=2x相交于点A.
(1)求直线l1的表达式;
(2)求点A的坐标;
(3)求△AOE的面积;
(4)当点P是直线l1上的一个动点时,过点P作y轴的平行线PB交直线l2于点B,当线段PB=3时,请直接写出P点的坐标.
七.(本题满分12分)
22.“绿叶”家政服务公司选派16名清洁工去打扫新装修的“海天”宾馆的房间,房间有大、小两种规格,每名清洁工一天能打扫4个大房间或5个小房间.设派x人去清扫大房间,其余人清扫小房间,清扫一个大房间工钱为80元,清扫一个小房间工钱为60元.
(1)写出家政服务公司每天的收入y(元)与x(人)之间的函数关系式:
(2)应该怎样安排这16名清洁工清扫?才能一天为“绿叶”家政服务公司创收5000元.
八.(本题满分14分)
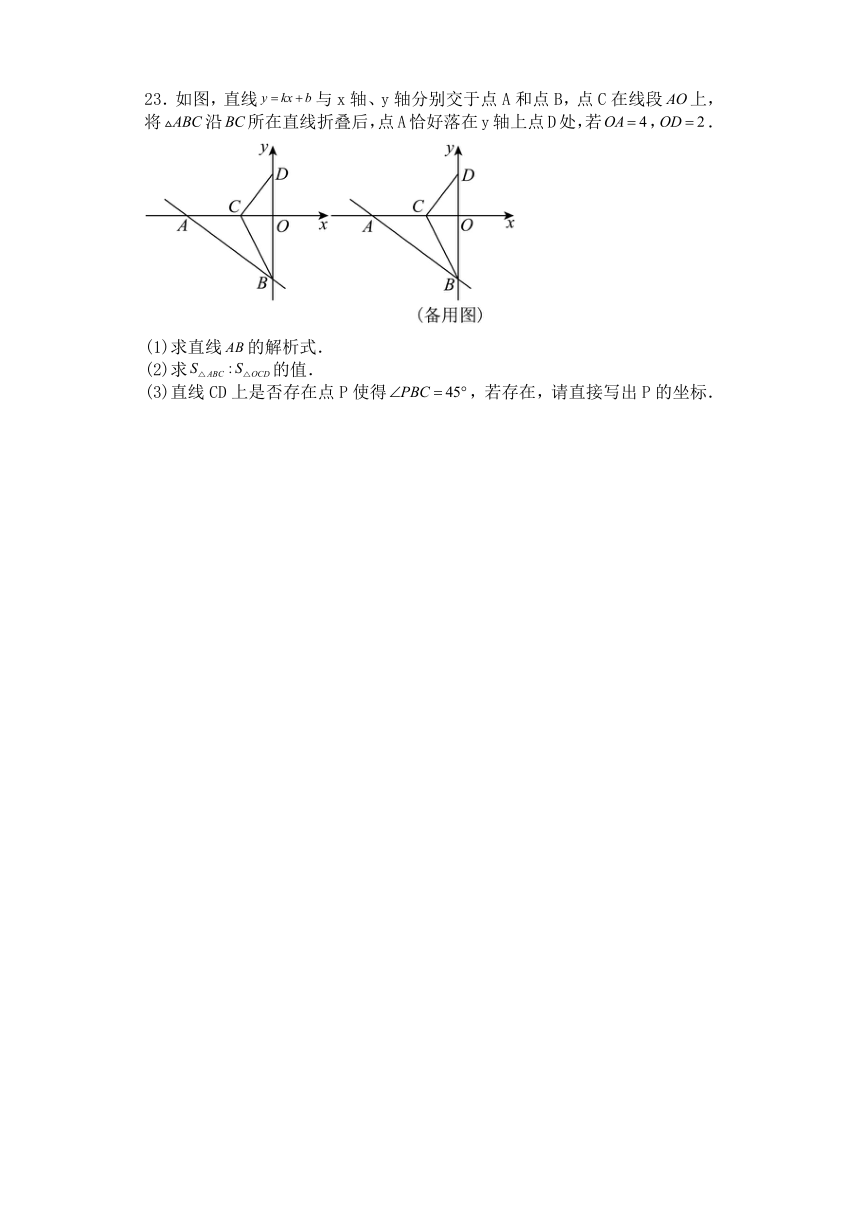
23.如图,直线与x轴、y轴分别交于点A和点B,点C在线段上,将沿所在直线折叠后,点A恰好落在y轴上点D处,若,.
(1)求直线的解析式.
(2)求的值.
(3)直线CD上是否存在点P使得,若存在,请直接写出P的坐标.
参考答案
1.C
【详解】解:根据一次函数的定义得,①;②;④,是一次函数,
故选:.
2.A
【详解】∵k=-3<0,b=-3<0,
∴一次函数图象经过第二、二、四象限,
故选A.
3.A
【详解】取直线y=2x上点(0,0),它向右平移1个单位,再向上平移1个单位后变为点(1,1)
设平移后的直线解析式为y=2x+b
由题意,点(1,1)在直线y=2x+b上,则有2+b=1
解得:b=-1
故y=2x-1
故选:A
4.C
【详解】解:A、k=1>0,y随x的增大而增大,故A错误;
B、k=>0,y随x的增大而增大,故B错误;
C、k=﹣1<0,y随x的增大而减小,故C正确;
D、k=3>0,y随x的增大而增大,故D错误;
故选:C
5.C
【详解】解:∵k=3>0,
∴在函数y=3x+2中,y随x的增大而增大,
∵ 1<2,
∴a<b,
故选:C.
6.A
【详解】解:由
解得
∵交点在第三象限,
∴,
解得
∴-4<b<8.
故选A.
7.B
【详解】解:先把点(m,n)代入函数y=2x+1,∴2m+1=n,即2m﹣n=﹣1,
∴4m﹣2n+1=2(2m﹣n)+1=2×(﹣1)+1=﹣1.
故选B.
8.D
【详解】解:∵y=3x+5中k=3>0,
∴y随x增大而增大,
∵6>-1>-9,
∴x2>x1>x3,
故选:D.
9.B
【详解】解:∵当时,
∴1-3m<0,
∴.
故选:B.
10.A
【详解】解:由函数y=ax+b的图象可知,
当x>0时,y>-2,故选项A正确;
当x<1时,y<0,故选项B错误;
当x<0时,y<-2,故选项C错误;
当x≥1时,y≥0,故选项D错误.
故选:A.
11.(0,-6)
【详解】解:
在y=2x-6中,令x=0可得y=-6,
∴直线y=2x-6与y轴的交点坐标为(0,-6),
故答案为:(0,-6).
12.y=﹣2x+3.
【详解】∵将直线y=﹣2x向上平移3个单位,
∴y=﹣2x+3,
即直线的AB的解析式是y=﹣2x+3.
故答案为y=﹣2x+3.
13.
【详解】解:将点和代入中得:
,解得:,
∴,
故答案为:.
14.二、四
【详解】∵函数y=(m﹣1)x|m|是正比例函数,
∴|m|=1,且m﹣1≠0, 解得:m=﹣1,
∴函数解析式为y=﹣2x,
∵k=﹣2<0,
∴该函数的图象经过第二、四象限.
故答案为:二、四.
15.(1)减小;(2),;(3)
【详解】如图所示:
(1)∵函数图像从左向右函数值向下递减,
∴的值随值的增大而减小;
故答案为:减小;
(2)由图可知图像与轴的交点坐标是,与轴的交点坐标是,
故答案为:,;
(3)由函数图像在x轴上及上方部分可知,当时,,
故答案为:.
16.见解析.
解:∵两直线平行,
∴5-3m=0.5,
∴m=1.5,
∴m-4=×1.5-4=-3,
∴此直线的解析式为:y= 0.5x-3.
17.(1)y=2x+4;(2)不在;(3)(3,10)或(-3,-2)
【详解】解:(1)把(-3,-2)代入y=kz+b得-3k+4=-2,解得k=2,
所以函数解析式为y=2x+4;
(2)当x=-5时,y=2x+4=2(-5)+4=-6,
所以点(-5,3)不在这个函数的图象上;
(3)当x=3时,y=2x+4=10,此时M点坐标为(3,10);
当x=-3时,y=2x+4=-2,此时M点坐标为(-3,-2).
18.(1)
(2)21
【详解】(1)解:由题意可设,,
,
,
当时,,当时,,
,解得,
,
即与之间的函数关系式为.
(2)解:将代入得:.
19.(1)
(2)4
【详解】(1)解:设一次函数的表达式为 y=kx+b(k≠0),
由题意,得,
解得
∴该一次函数解析式为;
(2)解:当 y=-3 时,,
解得 x=4,
∴当y=-3时,自变量x的值为4.
20.(1);(2)-1,-5,-2,,,,,-5,见解析;(3)见解析,-1【详解】,
把,;,代入,
得
解得,
的函数解析式为;
填表如下:
x 0 1 2 3 4 5 6
y
图象如图所示:
函数的图象如图所示,由图可知,当时,x的取值范围是.
21.(1)y=x+2;(2)(,);(3);(4)(﹣,)或(2,1)
【详解】解:(1)设直线11的解析式为y=kx+b,
把E(4,0),F(0,2)代入得,
解得k=﹣,b=2,
∴直线l1的表达式为y=﹣x+2;
(2)解
得
∴点A的坐标为(,);
(3)∵点E的坐标为(4,0),
∴OE=4,
∴△AOE的面积==;
(4)设P(a,﹣+2),则B(a,2a),
根据题意得|﹣+2﹣2a|=3,
解得a=﹣或a=2,
∴P点的坐标为(﹣,)或(2,1).
22.(1)
(2)应该安排这10名清洁工清扫大房间,6名清扫小房间
【详解】(1)有x人清扫大房间,则有人清扫小房间
∴
(2)解得:,
答:应该安排这10名清洁工清扫大房间,6名清扫小房间.
23.(1)
(2)
(3),
【详解】(1)由题知,设,则.
在中,,
即:,
,
∴,
又,
∴.
(2)设,则,
由折叠性质知:.
在中:,
∴,
∴.
∴,
∴,,
∴.
(3),,理由如下:
如图,当点P在第三象限内时,过C作于M,过M作轴,轴于E,F,
则,,
又∵
∴
∴,
∵轴,轴
∴为正方形
∴,
∴)
∴直线解析式为:,
∵两点坐标为:
∴直线解析式为:,
联立解得:,
∴
如图,当点P在第一象限内时,过C作于M,过M作轴,轴于E,F,
则,,
又∵
∴
∴,
∵轴,轴
∴为正方形
∴,
∴)
∴直线解析式为:,
∵两点坐标为:
∴直线解析式为:,
联立解得:,
∴
综上所述,或
(考试时间:120分钟 满分:150分)
一.选择题(本大题共10小题,每小题4分,满分40分)
1.下列函数:①;②;③;④,其中一次函数的个数是( )
A.1 B.2 C.3 D.4
2.函数y=-3x-3不经过第( )象限
A.一 B.二 C.三 D.四
3.将直线y=2x向右平移1个单位,再向上平移1个单位后,所得直线的表达式为( )
A.y=2x-1 B.y=2x C.y=2x+4 D.y=2x-2
4.函数值y随x的增大而减小的是( )
A.y=1+x B.y=x﹣1 C.y=﹣x+1 D.y=﹣2+3x
5.已知、是直线上的点,则a、b的大小关系为( )
A. B. C. D.a,b关系不确定
6.若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( )
A.-4
7.若点(m,n)在函数y=2x+1的图象上,则代数式4m﹣2n+1的值是( )
A.1 B.﹣1 C.2 D.﹣2
8.已知点,,都在直线上,则,,的值的大小关系是( ).
A. B. C. D.
9.一次函数的图像经过点和点,当时,则的取值范围( )
A. B. C. D.
10.在直角坐标平面内,一次函数y=ax+b的图象如图所示,那么下列说法正确的是( )
A.当时, B.当时, C.当时, D.当时,
二.填空题(共4小题,每小题5分,满分20分)
11.直线y=2x-6与y轴的交点坐标为________.
12.若将直线y=﹣2x向上平移3个单位后得到直线AB,那么直线AB的解析式是_____.
13.直线经过点和,则这条直线的表达式为___________.
14.若函数y=(m﹣1)x|m|是正比例函数,则该函数的图象经过第_____________象限.
三.(本大题共2小题,每小题8分,共16分)
15.作出函数的图像,并根据图像回答下列问题:
(1)y的值随x的增大而 ;
(2)图像与x轴的交点坐标是 ;与y轴的交点坐标是 ;
(3)当x 时,y≥0.
16.已知直线y=(5-3m)x+m-4与直线y=0.5x+6平行,求此直线的解析式.
四.(本大题共2小题,每小题8分,共16分)
17.一次函数的图象经过点(-3,-2).
(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
18.已知,且与x成正比例,与成正比例,当时,,当时,
(1)求出y与x之间的函数关系式;
(2)计算时,y的值.
五.(本大题共2小题,每小题10分,共20分)
19.已知是关于的一次函数,且当时,;当时,.
(1)求该一次函数的表达式;
(2)当时,求自变量的值.
20.已知函数,其自变量的取值范围是.当时,;当时,.
(1)根据给定的条件,求出的函数解析式;
(2)根据你所求的函数解析式,选取适当的自变量完成如表,并在下面的平面直角坐标系中描点并画出函数的大致图象:
(3)请画出的图象,并结合图象直接写出:当时,的取值范围是 .
六.(本题满分12分)
21.如图,在平面直角坐标系中,点E的坐标为(4,0),点F的坐标为(0,2),直线11经过点E和点F,直线l1与直线l2:y=2x相交于点A.
(1)求直线l1的表达式;
(2)求点A的坐标;
(3)求△AOE的面积;
(4)当点P是直线l1上的一个动点时,过点P作y轴的平行线PB交直线l2于点B,当线段PB=3时,请直接写出P点的坐标.
七.(本题满分12分)
22.“绿叶”家政服务公司选派16名清洁工去打扫新装修的“海天”宾馆的房间,房间有大、小两种规格,每名清洁工一天能打扫4个大房间或5个小房间.设派x人去清扫大房间,其余人清扫小房间,清扫一个大房间工钱为80元,清扫一个小房间工钱为60元.
(1)写出家政服务公司每天的收入y(元)与x(人)之间的函数关系式:
(2)应该怎样安排这16名清洁工清扫?才能一天为“绿叶”家政服务公司创收5000元.
八.(本题满分14分)
23.如图,直线与x轴、y轴分别交于点A和点B,点C在线段上,将沿所在直线折叠后,点A恰好落在y轴上点D处,若,.
(1)求直线的解析式.
(2)求的值.
(3)直线CD上是否存在点P使得,若存在,请直接写出P的坐标.
参考答案
1.C
【详解】解:根据一次函数的定义得,①;②;④,是一次函数,
故选:.
2.A
【详解】∵k=-3<0,b=-3<0,
∴一次函数图象经过第二、二、四象限,
故选A.
3.A
【详解】取直线y=2x上点(0,0),它向右平移1个单位,再向上平移1个单位后变为点(1,1)
设平移后的直线解析式为y=2x+b
由题意,点(1,1)在直线y=2x+b上,则有2+b=1
解得:b=-1
故y=2x-1
故选:A
4.C
【详解】解:A、k=1>0,y随x的增大而增大,故A错误;
B、k=>0,y随x的增大而增大,故B错误;
C、k=﹣1<0,y随x的增大而减小,故C正确;
D、k=3>0,y随x的增大而增大,故D错误;
故选:C
5.C
【详解】解:∵k=3>0,
∴在函数y=3x+2中,y随x的增大而增大,
∵ 1<2,
∴a<b,
故选:C.
6.A
【详解】解:由
解得
∵交点在第三象限,
∴,
解得
∴-4<b<8.
故选A.
7.B
【详解】解:先把点(m,n)代入函数y=2x+1,∴2m+1=n,即2m﹣n=﹣1,
∴4m﹣2n+1=2(2m﹣n)+1=2×(﹣1)+1=﹣1.
故选B.
8.D
【详解】解:∵y=3x+5中k=3>0,
∴y随x增大而增大,
∵6>-1>-9,
∴x2>x1>x3,
故选:D.
9.B
【详解】解:∵当时,
∴1-3m<0,
∴.
故选:B.
10.A
【详解】解:由函数y=ax+b的图象可知,
当x>0时,y>-2,故选项A正确;
当x<1时,y<0,故选项B错误;
当x<0时,y<-2,故选项C错误;
当x≥1时,y≥0,故选项D错误.
故选:A.
11.(0,-6)
【详解】解:
在y=2x-6中,令x=0可得y=-6,
∴直线y=2x-6与y轴的交点坐标为(0,-6),
故答案为:(0,-6).
12.y=﹣2x+3.
【详解】∵将直线y=﹣2x向上平移3个单位,
∴y=﹣2x+3,
即直线的AB的解析式是y=﹣2x+3.
故答案为y=﹣2x+3.
13.
【详解】解:将点和代入中得:
,解得:,
∴,
故答案为:.
14.二、四
【详解】∵函数y=(m﹣1)x|m|是正比例函数,
∴|m|=1,且m﹣1≠0, 解得:m=﹣1,
∴函数解析式为y=﹣2x,
∵k=﹣2<0,
∴该函数的图象经过第二、四象限.
故答案为:二、四.
15.(1)减小;(2),;(3)
【详解】如图所示:
(1)∵函数图像从左向右函数值向下递减,
∴的值随值的增大而减小;
故答案为:减小;
(2)由图可知图像与轴的交点坐标是,与轴的交点坐标是,
故答案为:,;
(3)由函数图像在x轴上及上方部分可知,当时,,
故答案为:.
16.见解析.
解:∵两直线平行,
∴5-3m=0.5,
∴m=1.5,
∴m-4=×1.5-4=-3,
∴此直线的解析式为:y= 0.5x-3.
17.(1)y=2x+4;(2)不在;(3)(3,10)或(-3,-2)
【详解】解:(1)把(-3,-2)代入y=kz+b得-3k+4=-2,解得k=2,
所以函数解析式为y=2x+4;
(2)当x=-5时,y=2x+4=2(-5)+4=-6,
所以点(-5,3)不在这个函数的图象上;
(3)当x=3时,y=2x+4=10,此时M点坐标为(3,10);
当x=-3时,y=2x+4=-2,此时M点坐标为(-3,-2).
18.(1)
(2)21
【详解】(1)解:由题意可设,,
,
,
当时,,当时,,
,解得,
,
即与之间的函数关系式为.
(2)解:将代入得:.
19.(1)
(2)4
【详解】(1)解:设一次函数的表达式为 y=kx+b(k≠0),
由题意,得,
解得
∴该一次函数解析式为;
(2)解:当 y=-3 时,,
解得 x=4,
∴当y=-3时,自变量x的值为4.
20.(1);(2)-1,-5,-2,,,,,-5,见解析;(3)见解析,-1
把,;,代入,
得
解得,
的函数解析式为;
填表如下:
x 0 1 2 3 4 5 6
y
图象如图所示:
函数的图象如图所示,由图可知,当时,x的取值范围是.
21.(1)y=x+2;(2)(,);(3);(4)(﹣,)或(2,1)
【详解】解:(1)设直线11的解析式为y=kx+b,
把E(4,0),F(0,2)代入得,
解得k=﹣,b=2,
∴直线l1的表达式为y=﹣x+2;
(2)解
得
∴点A的坐标为(,);
(3)∵点E的坐标为(4,0),
∴OE=4,
∴△AOE的面积==;
(4)设P(a,﹣+2),则B(a,2a),
根据题意得|﹣+2﹣2a|=3,
解得a=﹣或a=2,
∴P点的坐标为(﹣,)或(2,1).
22.(1)
(2)应该安排这10名清洁工清扫大房间,6名清扫小房间
【详解】(1)有x人清扫大房间,则有人清扫小房间
∴
(2)解得:,
答:应该安排这10名清洁工清扫大房间,6名清扫小房间.
23.(1)
(2)
(3),
【详解】(1)由题知,设,则.
在中,,
即:,
,
∴,
又,
∴.
(2)设,则,
由折叠性质知:.
在中:,
∴,
∴.
∴,
∴,,
∴.
(3),,理由如下:
如图,当点P在第三象限内时,过C作于M,过M作轴,轴于E,F,
则,,
又∵
∴
∴,
∵轴,轴
∴为正方形
∴,
∴)
∴直线解析式为:,
∵两点坐标为:
∴直线解析式为:,
联立解得:,
∴
如图,当点P在第一象限内时,过C作于M,过M作轴,轴于E,F,
则,,
又∵
∴
∴,
∵轴,轴
∴为正方形
∴,
∴)
∴直线解析式为:,
∵两点坐标为:
∴直线解析式为:,
联立解得:,
∴
综上所述,或
