第3章 一元一次方程 单元新测试与训练(含解析) 湘教版七年级上册数学
文档属性
| 名称 | 第3章 一元一次方程 单元新测试与训练(含解析) 湘教版七年级上册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 23:01:39 | ||
图片预览




文档简介
第3章 一元一次方程(单元新测试与训练)
湘教新版七年级上册数学
一.选择题(共9小题)
1.运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc D.如果ac=bc,那么a=b
2.下列方程的解是x=2的方程是( )
A.4x+8=0 B.﹣x+=0 C.x=2 D.1﹣3x=5
3.下列说法中,错误的是( )
A.若a=b,则a+2=b+2 B.若a=b,则﹣3a=﹣3b
C.若3a=2,则a= D.若2a=3b,则=
4.下列说法①若a+b=0,则a、b互为相反数;②若a、b互为倒数,则ab=1;③若ab>0,则a、b均大于0;④若|a|=a,则a一定为正数,其中正确的个数为( )
A.①④ B.①② C.①②④ D.①③④
5.下列方程变形中,正确的是( )
A.由3x=﹣4,系数化为1得x=
B.由5=2﹣x,移项得x=5﹣2
C.由 ,去分母得4(x﹣1)﹣3(2x+3)=1
D.由 3x﹣(2﹣4x)=5,去括号得3x+4x﹣2=5
6.小明到某文具店购买铅笔和中性笔.设购买铅笔的金额为x元,根据表格,下列方程错误的是( )
商品 单价(元/支) 购买数量/支 购买金额/元
铅笔 1.2 x
中性笔 3.5
总计 / 13 34
A.+=13 B.x+3.5(13﹣)=34
C.1.2(13﹣)=x D.3.5(13﹣)=34﹣x
7.一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.0.8(1+0.5)x=x+28 B.0.8(1+0.5)x=x﹣28
C.0.8(1+0.5x)=x﹣28 D.0.8(1+0.5x)=x+28
8.某中学的学生以4km/h的速度步行去某地参加社会公益活动.出发30min后,学校派一名通信员骑自行车以12km/h的速度去追赶队伍,通信员用多少时间可追上队伍?设通信员用x小时追上队伍,则可列方程( )
A.4x﹣2=12x B.4x+2=12x C.4x﹣0.5=12x D.4x+0.5=12x
9.甲、乙两人给一片花园浇水,甲单独做需要4小时完成浇水任务,乙单独做需要6小时完成浇水任务.现由甲、乙两人合作,完成浇水任务需要( )
A.2.4小时 B.3.2小时 C.5小时 D.10小时
二.填空题(共6小题)
10.若2a+3=0,则﹣4a﹣6= .
11.已知方程的解也是方程|3x﹣2|=b的解,则b= .
12.整式ax﹣b的值随x的取值不同而不同,下表是当x取不同值时对应的整式的值,则关于x的方程﹣ax+b=3的解是 .
x ﹣2 0 2
ax﹣b ﹣6 ﹣3 0
13.一套仪器由两个A部件和三个B部件构成.用1m3钢材可做40个A部件或240个B部件.现要用6m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?设应用xm3钢材做A部件,则可列一元一次方程为 .(方程不需要化简)
14.防范新冠病毒感染要养成戴口罩、勤洗手、多通风、常消毒等卫生习惯,其中对物体表面进行消毒可以采用浓度为75%的酒精.现有一瓶浓度为95%的酒精500mL,需将其加入适量的水,使浓度稀释为75%.设加水量为xmL,可列方程为 .
15.某商品按成本价提高50%后标价,再打8折出售,仍可获利280元,则该商品的成本价为 元.
三.解答题(共6小题)
16.解方程.
(1)﹣3(x+1)=9;
(2).
17.一种蔬菜在某市场上的批发价格如:
购买数量 不超过20千克 20千克以上但不超过40千克 40千克以上
价格 5元/千克 4元/千克 3元/千克
已知小明两次购买了此种蔬菜共70千克(第二次购买数量多于第一次).
(1)若第一次购买15千克,第二次购买55千克,则两次总费用为 元;
(2)若两次购买蔬菜的总费用为236元,求第一次、第二次分别购买此种蔬菜多少千克?
18.商店购进一批衬衫,每件衬衫的进价为40元,将每件衬衫提高20%的价格出售,当这批衬衫还剩下50件时,已收回这批衬衫的全部成本,还赚了400元.这批衬衫共购进多少件?
19.某市采用分段收费的方式按月计算每户家庭的水费,收费标准如表:
户月用水量(m3) 收费标准(元/m3)
不超过18m3 3.5
超过18m3,但不超过25m3的部分 5
超过25m3的部分 7
(1)小明家3月份用水量为20m3,应缴纳水费 元;
(2)设某户某月的用水量为xm3,应缴纳水费多少元?(用含x的代数式表示)
(3)小红家6月份和7月份的用水量共50m3,且7月份用水量比6月份多,这两个月共缴纳水费217元,则小红家6月份和7月份的用水量分别为 m3, m3.
20.从A地到B地是一段相距180千米先上坡,再下坡的公路.一辆汽车从A地驶往B地后再原路返回A地,汽车在上坡时的速度为30千米/时,下坡时的速度为40千米/时,从A地驶往B地所需时间比从B地驶往A地所需时间多0.5小时,求从A地驶往B地时上坡和下坡的路程.
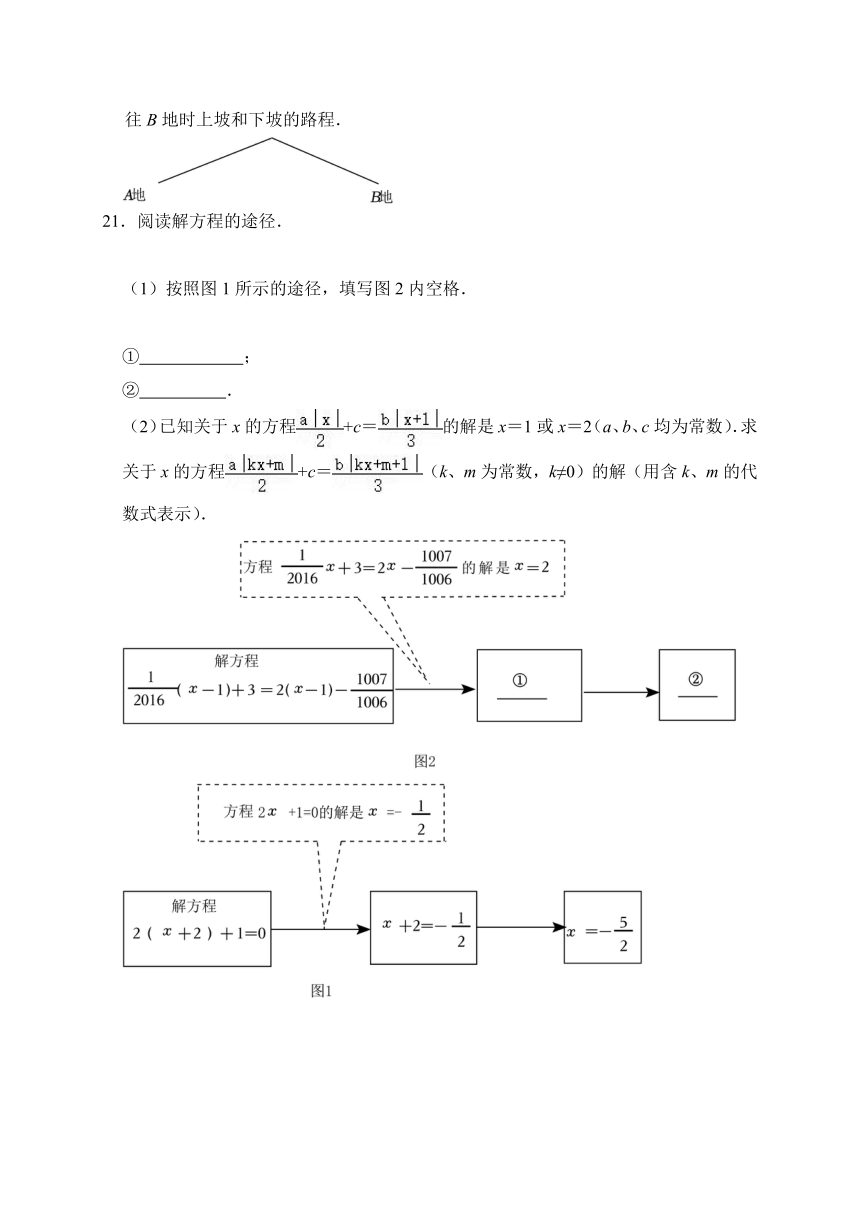
21.阅读解方程的途径.
(1)按照图1所示的途径,填写图2内空格.
① ;
② .
(2)已知关于x的方程+c=的解是x=1或x=2(a、b、c均为常数).求关于x的方程+c=(k、m为常数,k≠0)的解(用含k、m的代数式表示).
第3章 一元一次方程(单元新测试与训练)湘教新版七年级上册数学
参考答案与试题解析
一.选择题(共9小题)
1.运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc D.如果ac=bc,那么a=b
【答案】D
【解答】解:A、等号的两边都减c,故A正确;
B、等号的两边都加c,故B正确;
C、等号的两边都乘以c,故C正确;
D、c=0时无意义,故D错误;
故选:D.
2.下列方程的解是x=2的方程是( )
A.4x+8=0 B.﹣x+=0 C.x=2 D.1﹣3x=5
【答案】B
【解答】解:把x=2代入各方程验证可得出x=2是方程﹣x+=0的解.
故选:B.
3.下列说法中,错误的是( )
A.若a=b,则a+2=b+2 B.若a=b,则﹣3a=﹣3b
C.若3a=2,则a= D.若2a=3b,则=
【答案】C
【解答】解:A、若a=b,则a+2=b+2,正确,不符合题意;
B、若a=b,则﹣3a=﹣3b,正确,不符合题意;
C、若3a=2,则a=,原变形错误,符合题意;
D、若2a=3b,则=,正确,不符合题意.
故选:C.
4.下列说法①若a+b=0,则a、b互为相反数;②若a、b互为倒数,则ab=1;③若ab>0,则a、b均大于0;④若|a|=a,则a一定为正数,其中正确的个数为( )
A.①④ B.①② C.①②④ D.①③④
【答案】B
【解答】解:①若a+b=0,则a、b互为相反数,题干的说法是正确的;
②若a、b互为倒数,则ab=1,题干的说法是正确的;
③若ab>0,则a、b均大于0或均小于0,题干的说法是错误的;
④若|a|=a,则a一定为正数或0,题干的说法是错误的.
故选:B.
5.下列方程变形中,正确的是( )
A.由3x=﹣4,系数化为1得x=
B.由5=2﹣x,移项得x=5﹣2
C.由 ,去分母得4(x﹣1)﹣3(2x+3)=1
D.由 3x﹣(2﹣4x)=5,去括号得3x+4x﹣2=5
【答案】D
【解答】解:3x=﹣4,系数化为1,得x=﹣,故选项A错误,
5=2﹣x,移项,得x=2﹣5,故选项B错误,
由,去分母,得4(x﹣1)﹣3(2x+3)=24,故选项C错误,
由 3x﹣(2﹣4x)=5,去括号得,3x﹣2+4x=5,故选项D正确,
故选:D.
6.小明到某文具店购买铅笔和中性笔.设购买铅笔的金额为x元,根据表格,下列方程错误的是( )
商品 单价(元/支) 购买数量/支 购买金额/元
铅笔 1.2 x
中性笔 3.5
总计 / 13 34
A.+=13 B.x+3.5(13﹣)=34
C.1.2(13﹣)=x D.3.5(13﹣)=34﹣x
【答案】D
【解答】解:设购买铅笔的金额为x元,则购买中性笔的金额为(34﹣x)元,
根据题意得:+=13,1.2(13﹣)=x,x+3.5(13﹣)=34,
∴方程3.5(13﹣)=34﹣x不正确.
故选:D.
7.一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.0.8(1+0.5)x=x+28 B.0.8(1+0.5)x=x﹣28
C.0.8(1+0.5x)=x﹣28 D.0.8(1+0.5x)=x+28
【答案】A
【解答】解:设这件夹克衫的成本价是x元,
由题意得,0.8(1+50%)x﹣x=28,
即0.8(1+0.5)x=28+x.
故选:A.
8.某中学的学生以4km/h的速度步行去某地参加社会公益活动.出发30min后,学校派一名通信员骑自行车以12km/h的速度去追赶队伍,通信员用多少时间可追上队伍?设通信员用x小时追上队伍,则可列方程( )
A.4x﹣2=12x B.4x+2=12x C.4x﹣0.5=12x D.4x+0.5=12x
【答案】B
【解答】解:设通信员用多少小时可以追上队伍,
依题意可得:4x+2=12x.
故选:B.
9.甲、乙两人给一片花园浇水,甲单独做需要4小时完成浇水任务,乙单独做需要6小时完成浇水任务.现由甲、乙两人合作,完成浇水任务需要( )
A.2.4小时 B.3.2小时 C.5小时 D.10小时
【答案】A
【解答】解:设完成浇水任务需要x小时,依题意有
(+)x=1,
解得x=2.4.
故完成浇水任务需要2.4小时.
故选:A.
二.填空题(共6小题)
10.若2a+3=0,则﹣4a﹣6= 0 .
【答案】0.
【解答】解:∵2a+3=0,
∴﹣2a=3,
∴﹣4a=6,
∴﹣4a﹣6=6﹣6=0.
故答案为:0.
11.已知方程的解也是方程|3x﹣2|=b的解,则b= .
【答案】见试题解答内容
【解答】解:2(x﹣2)=20﹣5(x+3),
2x﹣4=20﹣5x﹣15,
7x=9,
解得:x=.
把x=代入方程|3x﹣2|=b得:|3×﹣2|=b,
解得:b=.
故答案为:.
12.整式ax﹣b的值随x的取值不同而不同,下表是当x取不同值时对应的整式的值,则关于x的方程﹣ax+b=3的解是 x=0 .
x ﹣2 0 2
ax﹣b ﹣6 ﹣3 0
【答案】x=0.
【解答】解:根据表格得:,
把②代入①得:﹣2a+3=﹣6,
解得:a=,
∴方程为﹣x+3=3,
解得:x=0.
故答案为:x=0.
13.一套仪器由两个A部件和三个B部件构成.用1m3钢材可做40个A部件或240个B部件.现要用6m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?设应用xm3钢材做A部件,则可列一元一次方程为 3×40x=240(6﹣x) .(方程不需要化简)
【答案】3×40x=240(6﹣x).
【解答】解:设用xm3钢材做A部件,则应用(6﹣x)m3钢材做B部件,则可配成这种仪器40x套,
根据题意,得3×40x=240(6﹣x).
故答案为:3×40x=240(6﹣x).
14.防范新冠病毒感染要养成戴口罩、勤洗手、多通风、常消毒等卫生习惯,其中对物体表面进行消毒可以采用浓度为75%的酒精.现有一瓶浓度为95%的酒精500mL,需将其加入适量的水,使浓度稀释为75%.设加水量为xmL,可列方程为 75%(500+x)=95%×500 .
【答案】75%(500+x)=95%×500.
【解答】解:设加水量为xmL,可列方程为:75%(500+x)=95%×500.
故答案为:75%(500+x)=95%×500.
15.某商品按成本价提高50%后标价,再打8折出售,仍可获利280元,则该商品的成本价为 1400 元.
【答案】1400.
【解答】解:设商品的成本价为x元,
由题意得:(1+50%)x 80%=x+280,
解得:x=1400.
答:这件商品的成本价为1400元.
故答案为:1400.
三.解答题(共6小题)
16.解方程.
(1)﹣3(x+1)=9;
(2).
【答案】(1)x=﹣4;
(2).
【解答】解:(1)﹣3(x+1)=9,
x+1=﹣3,
x=﹣3﹣1,
x=﹣4;
(2),
2(2x﹣1)﹣4=x﹣2,
4x﹣2﹣4=x﹣2,
4x﹣x=﹣2+2+4,
3x=4,
.
17.一种蔬菜在某市场上的批发价格如:
购买数量 不超过20千克 20千克以上但不超过40千克 40千克以上
价格 5元/千克 4元/千克 3元/千克
已知小明两次购买了此种蔬菜共70千克(第二次购买数量多于第一次).
(1)若第一次购买15千克,第二次购买55千克,则两次总费用为 240 元;
(2)若两次购买蔬菜的总费用为236元,求第一次、第二次分别购买此种蔬菜多少千克?
【答案】(1)240;
(2)第一次购买13千克,第二次购买57千克或第一次购买26千克,第二次购买44千克.
【解答】解:(1)总费用为:15×5+55×3=240(元).
故答案为:240;
(2)设第一次购买x千克,则第二次购买(70﹣x)千克,
①若第一次购买不超过20千克,第二次购买40千克以上,
由题意得:5x+3(70﹣x)=236,
解得x=13,
∴第二次购买(70﹣x)=57(千克),
②若第一次购买20千克以上但不超过40千克,第二次购买也为20千克以上但不超过40千克,
由题意得:4x+4(70﹣x)=236,
方程无解;
③若第一次20千克以上但不超过40千克,第二次购买40千克以上,
由题意得:4x+3(70﹣x)=236,
解得x=26,
∴第二次购买(70﹣x)=44(千克),
答:第一次购买13千克,第二次购买57千克或第一次购买26千克,第二次购买44千克.
18.商店购进一批衬衫,每件衬衫的进价为40元,将每件衬衫提高20%的价格出售,当这批衬衫还剩下50件时,已收回这批衬衫的全部成本,还赚了400元.这批衬衫共购进多少件?
【答案】这批衬衫共购进350件.
【解答】解:设批衬衫共购进x件,
由题意可得商品售价为40×(1+20%)=48(元),
所以(x﹣50)×48=40x+400,
解得:x=350.
答:这批衬衫共购进350件.
19.某市采用分段收费的方式按月计算每户家庭的水费,收费标准如表:
户月用水量(m3) 收费标准(元/m3)
不超过18m3 3.5
超过18m3,但不超过25m3的部分 5
超过25m3的部分 7
(1)小明家3月份用水量为20m3,应缴纳水费 73 元;
(2)设某户某月的用水量为xm3,应缴纳水费多少元?(用含x的代数式表示)
(3)小红家6月份和7月份的用水量共50m3,且7月份用水量比6月份多,这两个月共缴纳水费217元,则小红家6月份和7月份的用水量分别为 16 m3, 34 m3.
【答案】(1)73;
(2)应缴纳水费元;
(3)16,34.
【解答】解:(1)根据题意得:3.5×18+5×(20﹣18)
=3.5×18+5×2
=63+10
=73(元).
故答案为:73;
(2)根据题意得:当x≤18时,应缴纳水费3.5x元;
当18<x≤25时,应缴纳水费3.5×18+5(x﹣18)=(5x﹣27)元;
当x>25时,应缴纳水费3.5×18+5×(25﹣18)+7(x﹣25)=(7x﹣77)元.
∴应缴纳水费元;
(3)设小红家6月份的用水量为ym3,则7月份的用水量为(50﹣y)m3.
当y≤18时,3.5y+7(50﹣y)﹣77=217,
解得:y=16;
当18<y<25时,5y﹣27+7(50﹣y)﹣77=217,
解得:y=14.5(不符合题意,舍去).
∴y=16,
∴50﹣y=50﹣16=34,
∴小红家6月份的用水量为16m3,7月份的用水量为34m3.
故答案为:16,34.
20.从A地到B地是一段相距180千米先上坡,再下坡的公路.一辆汽车从A地驶往B地后再原路返回A地,汽车在上坡时的速度为30千米/时,下坡时的速度为40千米/时,从A地驶往B地所需时间比从B地驶往A地所需时间多0.5小时,求从A地驶往B地时上坡和下坡的路程.
【答案】从A地驶往B地时,上坡的路程为120km,下坡的路程为60km.
【解答】解:设从A地驶往B地时,上坡的路程为xkm,则下坡的路程为(180﹣x)km,
由题意,得:()﹣()=0.5,
解得x=120,
∴180﹣x=60,
答:从A地驶往B地时,上坡的路程为120km,下坡的路程为60km.
21.阅读解方程的途径.
(1)按照图1所示的途径,填写图2内空格.
① x﹣1=2 ;
② x=3 .
(2)已知关于x的方程+c=的解是x=1或x=2(a、b、c均为常数).求关于x的方程+c=(k、m为常数,k≠0)的解(用含k、m的代数式表示).
【答案】(1)①x﹣1=2;②x=3;(2)x1=,x2=.
【解答】解:(1)根据图1可得:①x﹣1=2;②x=3.
(2)由题意得:kx+m=1或kx+m=2,
解得:,.
湘教新版七年级上册数学
一.选择题(共9小题)
1.运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc D.如果ac=bc,那么a=b
2.下列方程的解是x=2的方程是( )
A.4x+8=0 B.﹣x+=0 C.x=2 D.1﹣3x=5
3.下列说法中,错误的是( )
A.若a=b,则a+2=b+2 B.若a=b,则﹣3a=﹣3b
C.若3a=2,则a= D.若2a=3b,则=
4.下列说法①若a+b=0,则a、b互为相反数;②若a、b互为倒数,则ab=1;③若ab>0,则a、b均大于0;④若|a|=a,则a一定为正数,其中正确的个数为( )
A.①④ B.①② C.①②④ D.①③④
5.下列方程变形中,正确的是( )
A.由3x=﹣4,系数化为1得x=
B.由5=2﹣x,移项得x=5﹣2
C.由 ,去分母得4(x﹣1)﹣3(2x+3)=1
D.由 3x﹣(2﹣4x)=5,去括号得3x+4x﹣2=5
6.小明到某文具店购买铅笔和中性笔.设购买铅笔的金额为x元,根据表格,下列方程错误的是( )
商品 单价(元/支) 购买数量/支 购买金额/元
铅笔 1.2 x
中性笔 3.5
总计 / 13 34
A.+=13 B.x+3.5(13﹣)=34
C.1.2(13﹣)=x D.3.5(13﹣)=34﹣x
7.一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.0.8(1+0.5)x=x+28 B.0.8(1+0.5)x=x﹣28
C.0.8(1+0.5x)=x﹣28 D.0.8(1+0.5x)=x+28
8.某中学的学生以4km/h的速度步行去某地参加社会公益活动.出发30min后,学校派一名通信员骑自行车以12km/h的速度去追赶队伍,通信员用多少时间可追上队伍?设通信员用x小时追上队伍,则可列方程( )
A.4x﹣2=12x B.4x+2=12x C.4x﹣0.5=12x D.4x+0.5=12x
9.甲、乙两人给一片花园浇水,甲单独做需要4小时完成浇水任务,乙单独做需要6小时完成浇水任务.现由甲、乙两人合作,完成浇水任务需要( )
A.2.4小时 B.3.2小时 C.5小时 D.10小时
二.填空题(共6小题)
10.若2a+3=0,则﹣4a﹣6= .
11.已知方程的解也是方程|3x﹣2|=b的解,则b= .
12.整式ax﹣b的值随x的取值不同而不同,下表是当x取不同值时对应的整式的值,则关于x的方程﹣ax+b=3的解是 .
x ﹣2 0 2
ax﹣b ﹣6 ﹣3 0
13.一套仪器由两个A部件和三个B部件构成.用1m3钢材可做40个A部件或240个B部件.现要用6m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?设应用xm3钢材做A部件,则可列一元一次方程为 .(方程不需要化简)
14.防范新冠病毒感染要养成戴口罩、勤洗手、多通风、常消毒等卫生习惯,其中对物体表面进行消毒可以采用浓度为75%的酒精.现有一瓶浓度为95%的酒精500mL,需将其加入适量的水,使浓度稀释为75%.设加水量为xmL,可列方程为 .
15.某商品按成本价提高50%后标价,再打8折出售,仍可获利280元,则该商品的成本价为 元.
三.解答题(共6小题)
16.解方程.
(1)﹣3(x+1)=9;
(2).
17.一种蔬菜在某市场上的批发价格如:
购买数量 不超过20千克 20千克以上但不超过40千克 40千克以上
价格 5元/千克 4元/千克 3元/千克
已知小明两次购买了此种蔬菜共70千克(第二次购买数量多于第一次).
(1)若第一次购买15千克,第二次购买55千克,则两次总费用为 元;
(2)若两次购买蔬菜的总费用为236元,求第一次、第二次分别购买此种蔬菜多少千克?
18.商店购进一批衬衫,每件衬衫的进价为40元,将每件衬衫提高20%的价格出售,当这批衬衫还剩下50件时,已收回这批衬衫的全部成本,还赚了400元.这批衬衫共购进多少件?
19.某市采用分段收费的方式按月计算每户家庭的水费,收费标准如表:
户月用水量(m3) 收费标准(元/m3)
不超过18m3 3.5
超过18m3,但不超过25m3的部分 5
超过25m3的部分 7
(1)小明家3月份用水量为20m3,应缴纳水费 元;
(2)设某户某月的用水量为xm3,应缴纳水费多少元?(用含x的代数式表示)
(3)小红家6月份和7月份的用水量共50m3,且7月份用水量比6月份多,这两个月共缴纳水费217元,则小红家6月份和7月份的用水量分别为 m3, m3.
20.从A地到B地是一段相距180千米先上坡,再下坡的公路.一辆汽车从A地驶往B地后再原路返回A地,汽车在上坡时的速度为30千米/时,下坡时的速度为40千米/时,从A地驶往B地所需时间比从B地驶往A地所需时间多0.5小时,求从A地驶往B地时上坡和下坡的路程.
21.阅读解方程的途径.
(1)按照图1所示的途径,填写图2内空格.
① ;
② .
(2)已知关于x的方程+c=的解是x=1或x=2(a、b、c均为常数).求关于x的方程+c=(k、m为常数,k≠0)的解(用含k、m的代数式表示).
第3章 一元一次方程(单元新测试与训练)湘教新版七年级上册数学
参考答案与试题解析
一.选择题(共9小题)
1.运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc D.如果ac=bc,那么a=b
【答案】D
【解答】解:A、等号的两边都减c,故A正确;
B、等号的两边都加c,故B正确;
C、等号的两边都乘以c,故C正确;
D、c=0时无意义,故D错误;
故选:D.
2.下列方程的解是x=2的方程是( )
A.4x+8=0 B.﹣x+=0 C.x=2 D.1﹣3x=5
【答案】B
【解答】解:把x=2代入各方程验证可得出x=2是方程﹣x+=0的解.
故选:B.
3.下列说法中,错误的是( )
A.若a=b,则a+2=b+2 B.若a=b,则﹣3a=﹣3b
C.若3a=2,则a= D.若2a=3b,则=
【答案】C
【解答】解:A、若a=b,则a+2=b+2,正确,不符合题意;
B、若a=b,则﹣3a=﹣3b,正确,不符合题意;
C、若3a=2,则a=,原变形错误,符合题意;
D、若2a=3b,则=,正确,不符合题意.
故选:C.
4.下列说法①若a+b=0,则a、b互为相反数;②若a、b互为倒数,则ab=1;③若ab>0,则a、b均大于0;④若|a|=a,则a一定为正数,其中正确的个数为( )
A.①④ B.①② C.①②④ D.①③④
【答案】B
【解答】解:①若a+b=0,则a、b互为相反数,题干的说法是正确的;
②若a、b互为倒数,则ab=1,题干的说法是正确的;
③若ab>0,则a、b均大于0或均小于0,题干的说法是错误的;
④若|a|=a,则a一定为正数或0,题干的说法是错误的.
故选:B.
5.下列方程变形中,正确的是( )
A.由3x=﹣4,系数化为1得x=
B.由5=2﹣x,移项得x=5﹣2
C.由 ,去分母得4(x﹣1)﹣3(2x+3)=1
D.由 3x﹣(2﹣4x)=5,去括号得3x+4x﹣2=5
【答案】D
【解答】解:3x=﹣4,系数化为1,得x=﹣,故选项A错误,
5=2﹣x,移项,得x=2﹣5,故选项B错误,
由,去分母,得4(x﹣1)﹣3(2x+3)=24,故选项C错误,
由 3x﹣(2﹣4x)=5,去括号得,3x﹣2+4x=5,故选项D正确,
故选:D.
6.小明到某文具店购买铅笔和中性笔.设购买铅笔的金额为x元,根据表格,下列方程错误的是( )
商品 单价(元/支) 购买数量/支 购买金额/元
铅笔 1.2 x
中性笔 3.5
总计 / 13 34
A.+=13 B.x+3.5(13﹣)=34
C.1.2(13﹣)=x D.3.5(13﹣)=34﹣x
【答案】D
【解答】解:设购买铅笔的金额为x元,则购买中性笔的金额为(34﹣x)元,
根据题意得:+=13,1.2(13﹣)=x,x+3.5(13﹣)=34,
∴方程3.5(13﹣)=34﹣x不正确.
故选:D.
7.一件夹克衫先按成本价提高50%标价,再将标价打8折出售,结果获利28元,如果设这件夹克衫的成本价是x元,那么根据题意,所列方程正确的是( )
A.0.8(1+0.5)x=x+28 B.0.8(1+0.5)x=x﹣28
C.0.8(1+0.5x)=x﹣28 D.0.8(1+0.5x)=x+28
【答案】A
【解答】解:设这件夹克衫的成本价是x元,
由题意得,0.8(1+50%)x﹣x=28,
即0.8(1+0.5)x=28+x.
故选:A.
8.某中学的学生以4km/h的速度步行去某地参加社会公益活动.出发30min后,学校派一名通信员骑自行车以12km/h的速度去追赶队伍,通信员用多少时间可追上队伍?设通信员用x小时追上队伍,则可列方程( )
A.4x﹣2=12x B.4x+2=12x C.4x﹣0.5=12x D.4x+0.5=12x
【答案】B
【解答】解:设通信员用多少小时可以追上队伍,
依题意可得:4x+2=12x.
故选:B.
9.甲、乙两人给一片花园浇水,甲单独做需要4小时完成浇水任务,乙单独做需要6小时完成浇水任务.现由甲、乙两人合作,完成浇水任务需要( )
A.2.4小时 B.3.2小时 C.5小时 D.10小时
【答案】A
【解答】解:设完成浇水任务需要x小时,依题意有
(+)x=1,
解得x=2.4.
故完成浇水任务需要2.4小时.
故选:A.
二.填空题(共6小题)
10.若2a+3=0,则﹣4a﹣6= 0 .
【答案】0.
【解答】解:∵2a+3=0,
∴﹣2a=3,
∴﹣4a=6,
∴﹣4a﹣6=6﹣6=0.
故答案为:0.
11.已知方程的解也是方程|3x﹣2|=b的解,则b= .
【答案】见试题解答内容
【解答】解:2(x﹣2)=20﹣5(x+3),
2x﹣4=20﹣5x﹣15,
7x=9,
解得:x=.
把x=代入方程|3x﹣2|=b得:|3×﹣2|=b,
解得:b=.
故答案为:.
12.整式ax﹣b的值随x的取值不同而不同,下表是当x取不同值时对应的整式的值,则关于x的方程﹣ax+b=3的解是 x=0 .
x ﹣2 0 2
ax﹣b ﹣6 ﹣3 0
【答案】x=0.
【解答】解:根据表格得:,
把②代入①得:﹣2a+3=﹣6,
解得:a=,
∴方程为﹣x+3=3,
解得:x=0.
故答案为:x=0.
13.一套仪器由两个A部件和三个B部件构成.用1m3钢材可做40个A部件或240个B部件.现要用6m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?设应用xm3钢材做A部件,则可列一元一次方程为 3×40x=240(6﹣x) .(方程不需要化简)
【答案】3×40x=240(6﹣x).
【解答】解:设用xm3钢材做A部件,则应用(6﹣x)m3钢材做B部件,则可配成这种仪器40x套,
根据题意,得3×40x=240(6﹣x).
故答案为:3×40x=240(6﹣x).
14.防范新冠病毒感染要养成戴口罩、勤洗手、多通风、常消毒等卫生习惯,其中对物体表面进行消毒可以采用浓度为75%的酒精.现有一瓶浓度为95%的酒精500mL,需将其加入适量的水,使浓度稀释为75%.设加水量为xmL,可列方程为 75%(500+x)=95%×500 .
【答案】75%(500+x)=95%×500.
【解答】解:设加水量为xmL,可列方程为:75%(500+x)=95%×500.
故答案为:75%(500+x)=95%×500.
15.某商品按成本价提高50%后标价,再打8折出售,仍可获利280元,则该商品的成本价为 1400 元.
【答案】1400.
【解答】解:设商品的成本价为x元,
由题意得:(1+50%)x 80%=x+280,
解得:x=1400.
答:这件商品的成本价为1400元.
故答案为:1400.
三.解答题(共6小题)
16.解方程.
(1)﹣3(x+1)=9;
(2).
【答案】(1)x=﹣4;
(2).
【解答】解:(1)﹣3(x+1)=9,
x+1=﹣3,
x=﹣3﹣1,
x=﹣4;
(2),
2(2x﹣1)﹣4=x﹣2,
4x﹣2﹣4=x﹣2,
4x﹣x=﹣2+2+4,
3x=4,
.
17.一种蔬菜在某市场上的批发价格如:
购买数量 不超过20千克 20千克以上但不超过40千克 40千克以上
价格 5元/千克 4元/千克 3元/千克
已知小明两次购买了此种蔬菜共70千克(第二次购买数量多于第一次).
(1)若第一次购买15千克,第二次购买55千克,则两次总费用为 240 元;
(2)若两次购买蔬菜的总费用为236元,求第一次、第二次分别购买此种蔬菜多少千克?
【答案】(1)240;
(2)第一次购买13千克,第二次购买57千克或第一次购买26千克,第二次购买44千克.
【解答】解:(1)总费用为:15×5+55×3=240(元).
故答案为:240;
(2)设第一次购买x千克,则第二次购买(70﹣x)千克,
①若第一次购买不超过20千克,第二次购买40千克以上,
由题意得:5x+3(70﹣x)=236,
解得x=13,
∴第二次购买(70﹣x)=57(千克),
②若第一次购买20千克以上但不超过40千克,第二次购买也为20千克以上但不超过40千克,
由题意得:4x+4(70﹣x)=236,
方程无解;
③若第一次20千克以上但不超过40千克,第二次购买40千克以上,
由题意得:4x+3(70﹣x)=236,
解得x=26,
∴第二次购买(70﹣x)=44(千克),
答:第一次购买13千克,第二次购买57千克或第一次购买26千克,第二次购买44千克.
18.商店购进一批衬衫,每件衬衫的进价为40元,将每件衬衫提高20%的价格出售,当这批衬衫还剩下50件时,已收回这批衬衫的全部成本,还赚了400元.这批衬衫共购进多少件?
【答案】这批衬衫共购进350件.
【解答】解:设批衬衫共购进x件,
由题意可得商品售价为40×(1+20%)=48(元),
所以(x﹣50)×48=40x+400,
解得:x=350.
答:这批衬衫共购进350件.
19.某市采用分段收费的方式按月计算每户家庭的水费,收费标准如表:
户月用水量(m3) 收费标准(元/m3)
不超过18m3 3.5
超过18m3,但不超过25m3的部分 5
超过25m3的部分 7
(1)小明家3月份用水量为20m3,应缴纳水费 73 元;
(2)设某户某月的用水量为xm3,应缴纳水费多少元?(用含x的代数式表示)
(3)小红家6月份和7月份的用水量共50m3,且7月份用水量比6月份多,这两个月共缴纳水费217元,则小红家6月份和7月份的用水量分别为 16 m3, 34 m3.
【答案】(1)73;
(2)应缴纳水费元;
(3)16,34.
【解答】解:(1)根据题意得:3.5×18+5×(20﹣18)
=3.5×18+5×2
=63+10
=73(元).
故答案为:73;
(2)根据题意得:当x≤18时,应缴纳水费3.5x元;
当18<x≤25时,应缴纳水费3.5×18+5(x﹣18)=(5x﹣27)元;
当x>25时,应缴纳水费3.5×18+5×(25﹣18)+7(x﹣25)=(7x﹣77)元.
∴应缴纳水费元;
(3)设小红家6月份的用水量为ym3,则7月份的用水量为(50﹣y)m3.
当y≤18时,3.5y+7(50﹣y)﹣77=217,
解得:y=16;
当18<y<25时,5y﹣27+7(50﹣y)﹣77=217,
解得:y=14.5(不符合题意,舍去).
∴y=16,
∴50﹣y=50﹣16=34,
∴小红家6月份的用水量为16m3,7月份的用水量为34m3.
故答案为:16,34.
20.从A地到B地是一段相距180千米先上坡,再下坡的公路.一辆汽车从A地驶往B地后再原路返回A地,汽车在上坡时的速度为30千米/时,下坡时的速度为40千米/时,从A地驶往B地所需时间比从B地驶往A地所需时间多0.5小时,求从A地驶往B地时上坡和下坡的路程.
【答案】从A地驶往B地时,上坡的路程为120km,下坡的路程为60km.
【解答】解:设从A地驶往B地时,上坡的路程为xkm,则下坡的路程为(180﹣x)km,
由题意,得:()﹣()=0.5,
解得x=120,
∴180﹣x=60,
答:从A地驶往B地时,上坡的路程为120km,下坡的路程为60km.
21.阅读解方程的途径.
(1)按照图1所示的途径,填写图2内空格.
① x﹣1=2 ;
② x=3 .
(2)已知关于x的方程+c=的解是x=1或x=2(a、b、c均为常数).求关于x的方程+c=(k、m为常数,k≠0)的解(用含k、m的代数式表示).
【答案】(1)①x﹣1=2;②x=3;(2)x1=,x2=.
【解答】解:(1)根据图1可得:①x﹣1=2;②x=3.
(2)由题意得:kx+m=1或kx+m=2,
解得:,.
同课章节目录
