3.1.2 等式的性质 课件(20张PPT)
文档属性
| 名称 | 3.1.2 等式的性质 课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:31:34 | ||
图片预览







文档简介
(共20张PPT)
人教版数学七年级上册——第三章
第三章
一元一次方程
3.1.2 等式
等式的性质 2
05
用等式的性质解方程
06
课堂小结
07
课后作业
08
教学目标
01
学习任务
02
等式的性质 1
03
新课导入
04
1.能判断一个数是正数还是负数,能用正数或负数表示生活中具有相反意义的量.
2.借助生活中的实例理解有理数的意义,体会负数引入的必要性和有理 数应用的广泛性.
3.培养学生主动探索,积极思考的学习兴趣培养学生积极思考,合作交流的意识和能 力.
教学目标
了解等式的性质;
利用等式的性质解方程;
通过对列方程的归纳,渗透“化归”思想。
学习任务
1.掌握等式的性质;
2.学会利用等式的性质解方程;
3.学会验证方程的解。
新课导入
想一想:将手边的物品用小天平称量,试着找出质量相等的物品.
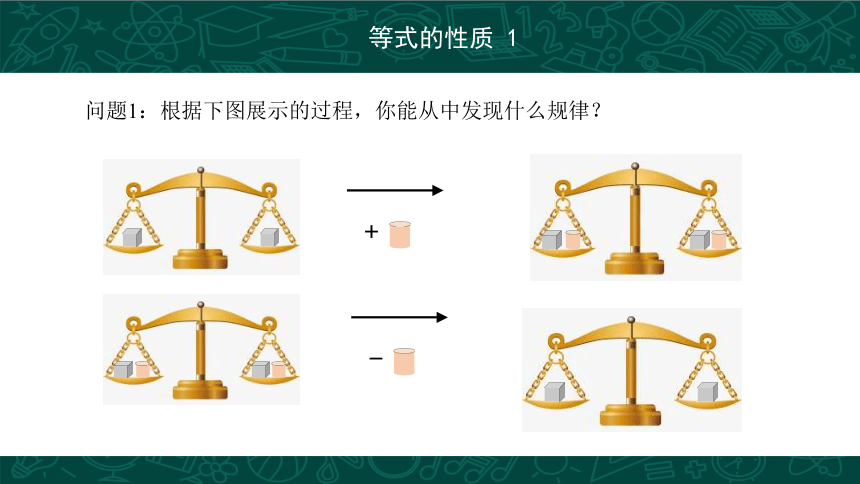
问题1:根据下图展示的过程,你能从中发现什么规律?
+
-
等式的性质 1
等式的性质 1
我们可以发现,平衡的天平两边同时都加(或减)相同的量,天平还保持平衡.
等式的性质1:
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c
等式的性质 2
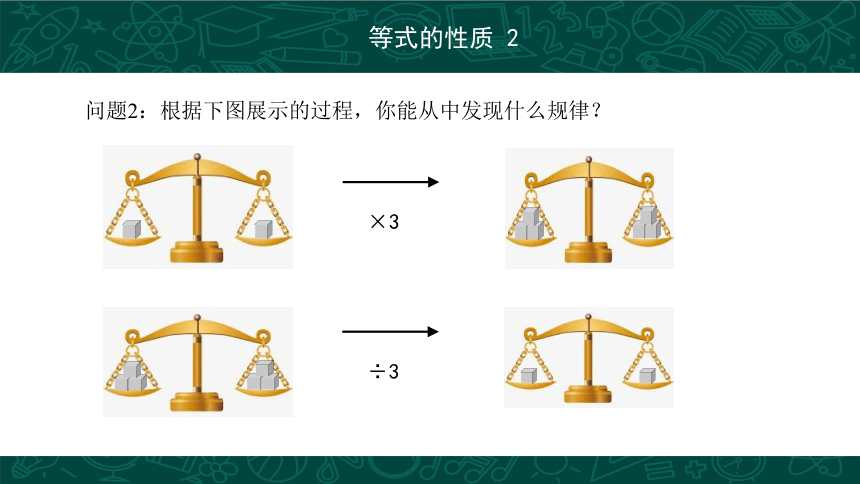
问题2:根据下图展示的过程,你能从中发现什么规律?
×3
÷3
等式的性质 2
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么
课堂练习
练习1.下列等式变形中,错误的是( )
A.由a=b,得a+4=b+4
B.由a=b,得a-3=b-3
C.由x+1=y+1,得x=y
D.由-2x=-2y,得x=-y
D
利用等式的性质解方程
例 利用等式的性质解下列方程:
(1) x + 7 = 26
解:两边减7,得
x + 7 -7= 26 -7
于是
x = 19
思考:如何利用等式的性质1 ,使方程x+7=26
转化为x=a(常数)的形式 ?
利用等式的性质解方程
例 利用等式的性质解下列方程:
(2) -5x = 20
解:两边除以-5,得
-5x÷(-5)= 20 ÷(-5)
于是
x = -4
利用等式的性质解方程
例 利用等式的性质解下列方程:
(3)
解:两边加5,得
化简,得
两边乘以-3,得
x = -27
总结:通过3个例题,我们可以知道:解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
检验方程的解
x + 7 = 26
x = 19
-5x = 20
x = -4
x = -27
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
19 + 7 = 26
-5×4 = 20
方程的左右两边相等,证明求得的解是原方程的解.
课堂练习
练习1.下列方程的变形,符合等式的性质的是( )
A.由2x-3=7,得2x=7-3
B.由3x-2=x+1,得3x-x=1-2
C.由-2x=5,得x=5+2
D.由-0.5x=1,得x=-2
D
课堂练习
练习2.如果等式7(x+2)=13(x+2)成立,那么x+2=______,即x=______.
练习3.若x-1=2024-y,则x+y=______.
0
-2
2023
课堂练习
练习4.利用等式的性质解方程:
(1)7+x=-3;
(2)-3x=27;
解:两边减7得
解:两边除以-3得
两边除以2得
-3x÷(-3)=27÷(-3)
x=-10
解:两边加6得
2x-6+6=10+6
x=8.
(3)2x-6=10.
7+x-7=-3-7
x=-9
2x=16
2x÷2=16÷2
课堂小结
等式的性质
内容
运用等式的性质解方程
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
课后作业
完成书本
第83页复习巩固的第4题、综合运用的第5题、第6题;
第84页的第7题、第8题。
人教版数学七年级上册
祝各位同学们学业进步,天天向上!
THE END
人教版数学七年级上册——第三章
第三章
一元一次方程
3.1.2 等式
等式的性质 2
05
用等式的性质解方程
06
课堂小结
07
课后作业
08
教学目标
01
学习任务
02
等式的性质 1
03
新课导入
04
1.能判断一个数是正数还是负数,能用正数或负数表示生活中具有相反意义的量.
2.借助生活中的实例理解有理数的意义,体会负数引入的必要性和有理 数应用的广泛性.
3.培养学生主动探索,积极思考的学习兴趣培养学生积极思考,合作交流的意识和能 力.
教学目标
了解等式的性质;
利用等式的性质解方程;
通过对列方程的归纳,渗透“化归”思想。
学习任务
1.掌握等式的性质;
2.学会利用等式的性质解方程;
3.学会验证方程的解。
新课导入
想一想:将手边的物品用小天平称量,试着找出质量相等的物品.
问题1:根据下图展示的过程,你能从中发现什么规律?
+
-
等式的性质 1
等式的性质 1
我们可以发现,平衡的天平两边同时都加(或减)相同的量,天平还保持平衡.
等式的性质1:
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c
等式的性质 2
问题2:根据下图展示的过程,你能从中发现什么规律?
×3
÷3
等式的性质 2
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么
课堂练习
练习1.下列等式变形中,错误的是( )
A.由a=b,得a+4=b+4
B.由a=b,得a-3=b-3
C.由x+1=y+1,得x=y
D.由-2x=-2y,得x=-y
D
利用等式的性质解方程
例 利用等式的性质解下列方程:
(1) x + 7 = 26
解:两边减7,得
x + 7 -7= 26 -7
于是
x = 19
思考:如何利用等式的性质1 ,使方程x+7=26
转化为x=a(常数)的形式 ?
利用等式的性质解方程
例 利用等式的性质解下列方程:
(2) -5x = 20
解:两边除以-5,得
-5x÷(-5)= 20 ÷(-5)
于是
x = -4
利用等式的性质解方程
例 利用等式的性质解下列方程:
(3)
解:两边加5,得
化简,得
两边乘以-3,得
x = -27
总结:通过3个例题,我们可以知道:解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
检验方程的解
x + 7 = 26
x = 19
-5x = 20
x = -4
x = -27
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
19 + 7 = 26
-5×4 = 20
方程的左右两边相等,证明求得的解是原方程的解.
课堂练习
练习1.下列方程的变形,符合等式的性质的是( )
A.由2x-3=7,得2x=7-3
B.由3x-2=x+1,得3x-x=1-2
C.由-2x=5,得x=5+2
D.由-0.5x=1,得x=-2
D
课堂练习
练习2.如果等式7(x+2)=13(x+2)成立,那么x+2=______,即x=______.
练习3.若x-1=2024-y,则x+y=______.
0
-2
2023
课堂练习
练习4.利用等式的性质解方程:
(1)7+x=-3;
(2)-3x=27;
解:两边减7得
解:两边除以-3得
两边除以2得
-3x÷(-3)=27÷(-3)
x=-10
解:两边加6得
2x-6+6=10+6
x=8.
(3)2x-6=10.
7+x-7=-3-7
x=-9
2x=16
2x÷2=16÷2
课堂小结
等式的性质
内容
运用等式的性质解方程
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
课后作业
完成书本
第83页复习巩固的第4题、综合运用的第5题、第6题;
第84页的第7题、第8题。
人教版数学七年级上册
祝各位同学们学业进步,天天向上!
THE END
