17.2因式分解法解一元二次方程(第2课时) 课件(34张PPT)
文档属性
| 名称 | 17.2因式分解法解一元二次方程(第2课时) 课件(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
沪教版八年级上册
第 17 章一元二次方程
17.2因式分解法解一元二次方程(第2课时)
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
6 随堂检测
7 课堂小结
5 题型讲解
学习目标
1、会使用因式分解的方法解某些一元二次方程。
2、经历因式分解法把一元二次方程化为两个一元一次方程的过程,体会“降次”和“转化”的思想。
(2)因式分解有哪些方法?
1. (1)什么是因式分解?
①提公因式法
②公式法
平方差公式
完全平方公式
③十字相乘法
把一个多项式分解成几个整式乘积的形式叫做因式分解.
复习引入
特殊的一元二次方程
一元一次方程
开平方
降次 化归
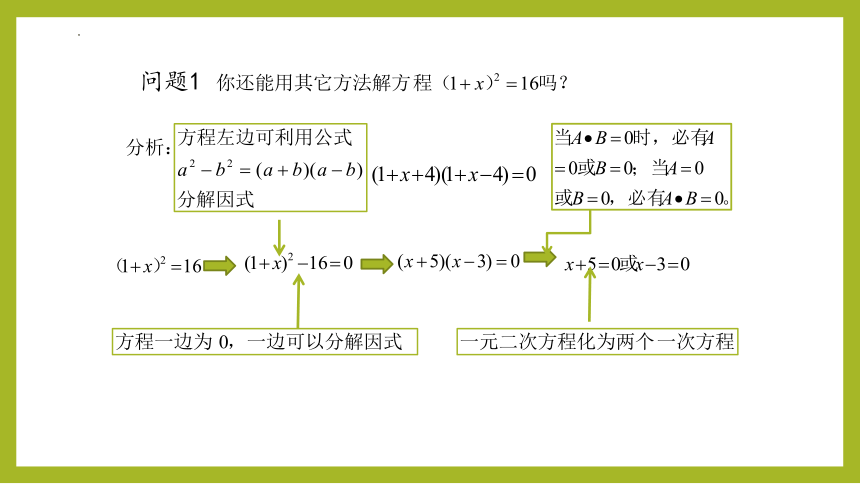
问题1
问题1
问题2
新课讲解
例题1
1.因式分解法解一元二次方程
(1)x2-3x=0 (2)25x2=16
1 解下列方程:
解:将原方程的左边分解因式得:
则x=0,或x-3=0
解得x1=0,x2=3
解:移项,得 25x2-16=0
(5x+4)(5x-4)=0
则5x+4=0或5x-4=0
等号左边能不能进行因式分解?
x(x-3)=0
将方程的左边分解因式得:
练一练
要点归纳
因式分解法的概念
因式分解法的基本步骤
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
简记歌诀:
右化零 左分解
两因式 各求解
当一元二次方程的一边是0,而另一边易于分解成两个一次因式的乘积时,我们就可以用分解因式的方法求解.这种用分解因式解一元二次方程的方法称为因式分解法.
例题2
例题3
2 解下列一元二次方程:
(1)(x-5) (3x-2)=10;
解: 化简方程,得 3x2-17x=0.
将方程的左边分解因式,
得 x(3x-17)=0,
则x=0 ,或3x-17=0,
解得x1=0,x2=
(2)(3x-4)2 = (4x-3)2.
解:移项,得(3x-4)2-(4x-3)2=0.
将方程的左边分解因式,得
[(3x-4)+(4x-3)][(3x-4)-(4x-3)]=0,
即 (7x-7) (-x-1)=0.
则7x-7=0,或-x-1=0.
解得x1=1, x2=-1.
这种情况下可以直接用因式分解法吗?
练一练
3.解下列方程:
(1)(2x + 3)2 = 4 (2x + 3) ; (2)(x - 2) 2 = (2x + 3) 2.
解:(2x + 3)2 - 4 (2x + 3) =0 ,
(2x + 3) (2x + 3 - 4) = 0,
(2x + 3) (2x - 1) = 0.
∴ 2x + 3 = 0 或 2x - 1 = 0.
解:(x - 2)2 - (2x + 3) 2 =0,
( x -2+ 2x+ 3) (x -2 - 2x - 3)=0,
(3x + 1)(x + 5) = 0.
∴ 3x + 1 = 0 或 x + 5 = 0.
练一练
这一步利用什么方法分解因式?
练一练
2. 因式分解法应用
几种常见的用因式分解法求解的方程
(1)形如x2 +bx = 0 的一元二次方程,将左边运用提公因式法因式分解为
x(x+b)= 0,则x = 0 或x+b = 0,即x1= 0, x2 = -b.
(2)形如x2 - a2 = 0 的一元二次方程,将左边用平方差公式因式分解为(x+a)(x-a)= 0,则x+a = 0 或x-a = 0,即x1 = -a, x2 = a.
(3)形如x2 ±2ax+ a2 = 0 的一元二次方程,将左边用完全平方公式因式分解为(x± a )2= 0,则① x+a = 0,即x1 = x2 = -a. ② x-a = 0,即x1 = x2 = a.
(4)形如x2 +(a+b)x+ab = 0 的一元二次方程,将其左边因式分解, 则方程化为(x+a)(x+b)= 0,所以x+a = 0 或x+b = 0,即x1 = -a, x2 = -b.
归纳总结
1、(口答)说出下列方程的根:
课本练习
√
×
×
1.一元二次方程(x-3)(x-5)=0的两根分别为( )
A.3,-5 B.-3,-5 C.-3,5 D.3,5
2.一元二次方程x(x-2)=2-x的根是( )
A.-1 B.2 C.1和2 D.-1和2
3.方程x2-3x+2=0的根是 .
D
D
x1=1, x2=2
随堂检测
5.△ABC的三边长都是方程x2-6x+8=0的解,则△ABC的周长是
( )
A.10 B.12
C.6或10或12 D.6或 8或10或12
4.已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是( )
A.5 B.7 C.5或7 D.10
B
C
6.解方程:
(1)x(x-2)=x-2; (2)9(x+1)2-16(x-2)2=0;
解:x(x-2)=x-2,
x(x-2)-(x-2)=0,
(x-1)(x-2)=0,
∴x1=1,x2=2.
解:9(x+1)2-16(x-2)2=0,
[3(x+1)+4(x-2)][3(x+1)-4(x-2)]=0,
(7x-5)(-x+11)=0,
(1)在上述解法中,第 步有问题,问题在于 ;
(2)请将正确的解法写在下面.
③
2x-1可能等于0
因式分解法
概念
步骤
简记歌诀:
右化零 左分解
两因式 各求解
如果a ·b=0,那么a=0或b=0.
原理
将方程左边因式分解,右边=0.
因式分解的方法有
ma+mb+mc=m(a+b+c);
a2 ±2ab+b2=(a ±b)2;
a2 -b2=(a +b)(a -b).
课堂小结
解一元二次方程的方法的选择技巧
若一元二次方程可化为 (mx+n)2=p(m≠0,p≥0) 的形式,则宜选用直接开平方法;
若一元二次方程的二次项系数为 1,一次项系数为偶数,则宜选用配方法;
若一元二次方程整理后右边为 0,且左边能进行因式分解,则宜选用因式分解法;
若直接开平方法、配方法、因式分解法都不简便,则宜选用公式法。
沪教版八年级上册
第 17 章一元二次方程
17.2因式分解法解一元二次方程(第2课时)
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
6 随堂检测
7 课堂小结
5 题型讲解
学习目标
1、会使用因式分解的方法解某些一元二次方程。
2、经历因式分解法把一元二次方程化为两个一元一次方程的过程,体会“降次”和“转化”的思想。
(2)因式分解有哪些方法?
1. (1)什么是因式分解?
①提公因式法
②公式法
平方差公式
完全平方公式
③十字相乘法
把一个多项式分解成几个整式乘积的形式叫做因式分解.
复习引入
特殊的一元二次方程
一元一次方程
开平方
降次 化归
问题1
问题1
问题2
新课讲解
例题1
1.因式分解法解一元二次方程
(1)x2-3x=0 (2)25x2=16
1 解下列方程:
解:将原方程的左边分解因式得:
则x=0,或x-3=0
解得x1=0,x2=3
解:移项,得 25x2-16=0
(5x+4)(5x-4)=0
则5x+4=0或5x-4=0
等号左边能不能进行因式分解?
x(x-3)=0
将方程的左边分解因式得:
练一练
要点归纳
因式分解法的概念
因式分解法的基本步骤
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
简记歌诀:
右化零 左分解
两因式 各求解
当一元二次方程的一边是0,而另一边易于分解成两个一次因式的乘积时,我们就可以用分解因式的方法求解.这种用分解因式解一元二次方程的方法称为因式分解法.
例题2
例题3
2 解下列一元二次方程:
(1)(x-5) (3x-2)=10;
解: 化简方程,得 3x2-17x=0.
将方程的左边分解因式,
得 x(3x-17)=0,
则x=0 ,或3x-17=0,
解得x1=0,x2=
(2)(3x-4)2 = (4x-3)2.
解:移项,得(3x-4)2-(4x-3)2=0.
将方程的左边分解因式,得
[(3x-4)+(4x-3)][(3x-4)-(4x-3)]=0,
即 (7x-7) (-x-1)=0.
则7x-7=0,或-x-1=0.
解得x1=1, x2=-1.
这种情况下可以直接用因式分解法吗?
练一练
3.解下列方程:
(1)(2x + 3)2 = 4 (2x + 3) ; (2)(x - 2) 2 = (2x + 3) 2.
解:(2x + 3)2 - 4 (2x + 3) =0 ,
(2x + 3) (2x + 3 - 4) = 0,
(2x + 3) (2x - 1) = 0.
∴ 2x + 3 = 0 或 2x - 1 = 0.
解:(x - 2)2 - (2x + 3) 2 =0,
( x -2+ 2x+ 3) (x -2 - 2x - 3)=0,
(3x + 1)(x + 5) = 0.
∴ 3x + 1 = 0 或 x + 5 = 0.
练一练
这一步利用什么方法分解因式?
练一练
2. 因式分解法应用
几种常见的用因式分解法求解的方程
(1)形如x2 +bx = 0 的一元二次方程,将左边运用提公因式法因式分解为
x(x+b)= 0,则x = 0 或x+b = 0,即x1= 0, x2 = -b.
(2)形如x2 - a2 = 0 的一元二次方程,将左边用平方差公式因式分解为(x+a)(x-a)= 0,则x+a = 0 或x-a = 0,即x1 = -a, x2 = a.
(3)形如x2 ±2ax+ a2 = 0 的一元二次方程,将左边用完全平方公式因式分解为(x± a )2= 0,则① x+a = 0,即x1 = x2 = -a. ② x-a = 0,即x1 = x2 = a.
(4)形如x2 +(a+b)x+ab = 0 的一元二次方程,将其左边因式分解, 则方程化为(x+a)(x+b)= 0,所以x+a = 0 或x+b = 0,即x1 = -a, x2 = -b.
归纳总结
1、(口答)说出下列方程的根:
课本练习
√
×
×
1.一元二次方程(x-3)(x-5)=0的两根分别为( )
A.3,-5 B.-3,-5 C.-3,5 D.3,5
2.一元二次方程x(x-2)=2-x的根是( )
A.-1 B.2 C.1和2 D.-1和2
3.方程x2-3x+2=0的根是 .
D
D
x1=1, x2=2
随堂检测
5.△ABC的三边长都是方程x2-6x+8=0的解,则△ABC的周长是
( )
A.10 B.12
C.6或10或12 D.6或 8或10或12
4.已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是( )
A.5 B.7 C.5或7 D.10
B
C
6.解方程:
(1)x(x-2)=x-2; (2)9(x+1)2-16(x-2)2=0;
解:x(x-2)=x-2,
x(x-2)-(x-2)=0,
(x-1)(x-2)=0,
∴x1=1,x2=2.
解:9(x+1)2-16(x-2)2=0,
[3(x+1)+4(x-2)][3(x+1)-4(x-2)]=0,
(7x-5)(-x+11)=0,
(1)在上述解法中,第 步有问题,问题在于 ;
(2)请将正确的解法写在下面.
③
2x-1可能等于0
因式分解法
概念
步骤
简记歌诀:
右化零 左分解
两因式 各求解
如果a ·b=0,那么a=0或b=0.
原理
将方程左边因式分解,右边=0.
因式分解的方法有
ma+mb+mc=m(a+b+c);
a2 ±2ab+b2=(a ±b)2;
a2 -b2=(a +b)(a -b).
课堂小结
解一元二次方程的方法的选择技巧
若一元二次方程可化为 (mx+n)2=p(m≠0,p≥0) 的形式,则宜选用直接开平方法;
若一元二次方程的二次项系数为 1,一次项系数为偶数,则宜选用配方法;
若一元二次方程整理后右边为 0,且左边能进行因式分解,则宜选用因式分解法;
若直接开平方法、配方法、因式分解法都不简便,则宜选用公式法。
