6.3一次函数的图象 第1课时 正比例函数的图象及性质 同步练习(含解析)
文档属性
| 名称 | 6.3一次函数的图象 第1课时 正比例函数的图象及性质 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
3 一次函数的图象
第1课时 正比例函数的图象及性质
基础夯实
知识点一 正比例函数的图象
1.下列四个点,在正比例函数 的图象上的点是( )
A.(2,5) B.(5,2) C.(2,-5) D.(5,-2)
2.正方形的边长a与周长之间的函数关系式为=4a,其图象是图中的( )
3.点(3,-5)在正比例函数y=kx(k≠0)的图象上,则k的值为 ( )
A.-15 B.15
4.经过以下一组点可以画出函数y=2x图象的是( )
A.(0,0)和(2,1) B.(1,2)和(-1,-2) C.(1,2)和(2,1) D.(-1,2)和(1,2)
知识点二 正比例函数的性质
5.关于正比例函数 y=-2x,下列结论正确的是( )
A.图象必经过点(-1,-2) B.图象经过第一、三象限
C.y随x的增大而减小 D.不论x取何值,总有 y0
6.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则 m等于( )
A.2 B.-2 C.4 D.-4
7.已知正比例函数y=kx的图象经过点(3,-6).
(1)求这个函数表达式;
(2)画出这个函数图象;
(3)判断点 A(4,-2)、点 B(-1.5,3)是否在这个函数图象上;
(4)图象上的两点 C(x ,y ),D(x ,y ),如果x x ,比较y ,y 的大小.
易错点 求正比例函数关系式时易忽视隐含条件而产生多解
8.已知函数 是正比例函数.
(1)若函数关系式中 y随x的增大而减小,求m的值;
(2)若函数的图象过第一、三象限,求 m的值.
能力提升
9.已知正比例函数 y=kx,当x每增加2时,y减少3,则k的值为( )
10.如图,三个正比例函数的图象分别对应函数关系式:,将a,b,c从小到大排列并用“”连接为( )
11.已知正比例函数y=(2m-1)x的图象上两点A(x ,y ),B(x ,y ),当xy y ,那么m的取值范围是( )
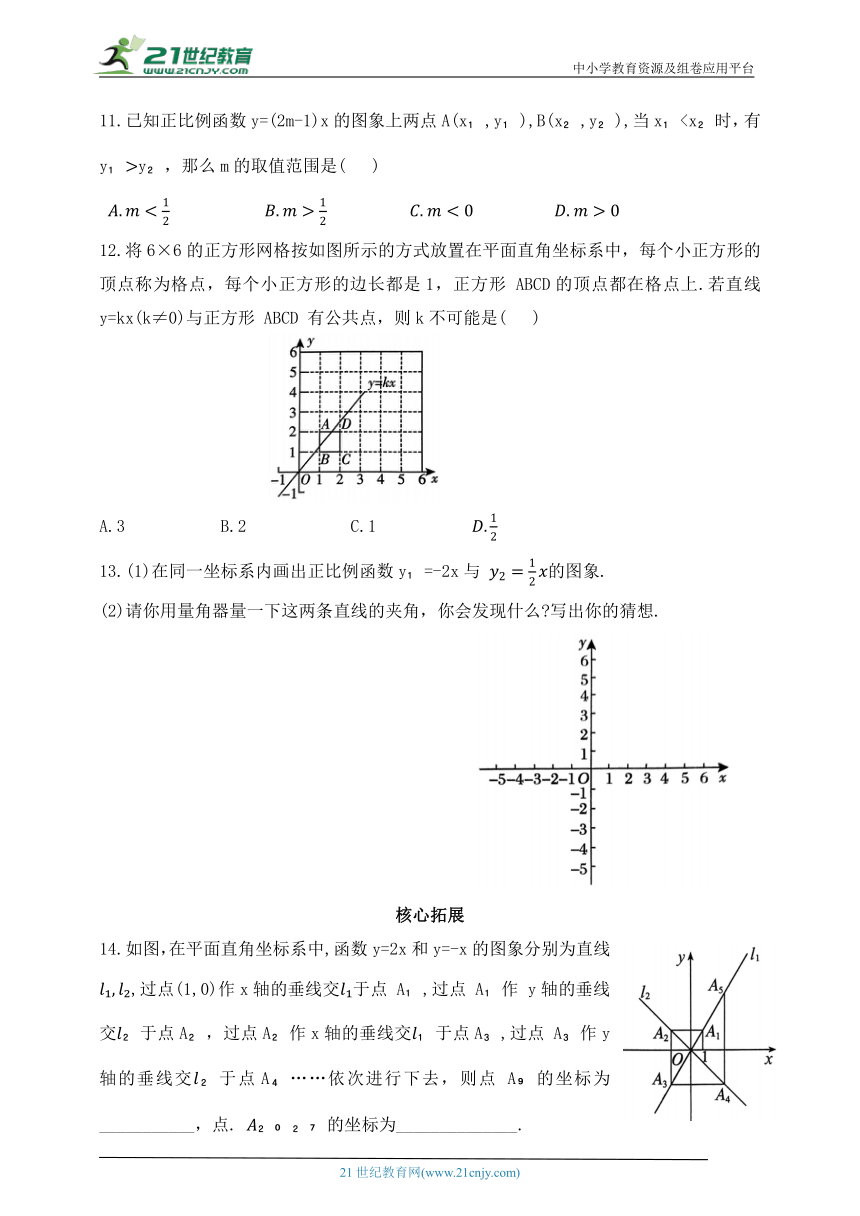
12.将6×6的正方形网格按如图所示的方式放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形 ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形 ABCD 有公共点,则k不可能是( )
A.3 B.2 C.1
13.(1)在同一坐标系内画出正比例函数y =-2x与 的图象.
(2)请你用量角器量一下这两条直线的夹角,你会发现什么 写出你的猜想.
核心拓展
14.如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线,过点(1,0)作x轴的垂线交于点 A ,过点 A 作 y轴的垂线交 于点A ,过点A 作x轴的垂线交 于点A ,过点 A 作y轴的垂线交 于点A ……依次进行下去,则点 A 的坐标为___________,点. 的坐标为______________.
15.已知函数
(1)动手操作:在同一坐标系内画出这四个函数的图象.
(2)探索发现:观察这些函数的图象可以发现,随|k|的增大,直线与 y轴的位置关系有何变化
(3)灵活运用:已知正比例函数y =k x,y =k x在同一坐标系中的图象如图所示,判定k 与k 的大小关系.
参考答案
1. D 2. C
3. D【解析】因为点(3,-5)在正比例函数y=kx(k≠0)的图象上,所以-5=3k,解得 故选 D.
4. B 5. C
6. B【解析】把x=m,y=4代入y=mx中,得m =4,解得m=±2.
因为y的值随x值的增大而减小,所以m=-2.故选 B.
7.解:(1)将点(3,-6)代入y=kx,得-6=3k,解得k=-2.所以函数表达式为y=-2x.
(2)函数图象过点(0,0),(1,-2),描点,连线函数图象如图所示.
(3)将点 A(4,-2)、点 B(-1.5,3)的坐标分别代入表达式,得-2≠-2×4,3=-2×(-1.5).
故点A不在函数图象上,点B在函数图象上.
(4)由于k=-2<0,故y随x的增大而减小,可得y8.解:(1)由题意知m -3=1,且m-1<0.故m=-2.
(2)由题意知m -3=1,且m-1>0.故m=2.
9. C【解析】由当x每增加2时,y减少3,知x每增加1时,y减少 所以k的值为 故选 C.
10. D【解析】根据三个函数图象所在象限可得 a<0,b>0,c>0,再根据直线越陡,|k|越大,则b>c.则b>c>a,即a<c<b.
11. A
12. A 【解析】由图可知,A(1,2),C(2,1),所以当直线y=kx过点A时,k=2;当直线过点C时,2k=1,即 满足 所以k不可能是3.
13.解:(1)如图所示.
(2)两条直线的夹角为90°;当两个一次函数的一次项系数之积为-1时,两条直线的夹角为90°,即两直线垂直.
14.(16,32) (-2 ,-2 )
【解析】当x=1时,y=2,所以点A 的坐标为(1,2);
当y=-x=2时,x=-2,所以点A 的坐标为(-2,2);
同理可得:A (-2,-4),A (4,-4),A (4,8),A (-8,8),A (-8,-16),A (16,-16),
A (16,32),…,所以
,(n为自然数).
因为2027=506×4+3,所以点A 的坐标为
即(-2 0 ,-2 ).
故答案为(16,32);(-2 ,-2 ).
15.解:(1)画图略.
(2)观察函数的图象可以发现,|k|的值越大,直线与y轴的夹角越小.
(3)由(2)中的规律可知,|k |>|k |,且k <0,k <0,所以k <k .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
3 一次函数的图象
第1课时 正比例函数的图象及性质
基础夯实
知识点一 正比例函数的图象
1.下列四个点,在正比例函数 的图象上的点是( )
A.(2,5) B.(5,2) C.(2,-5) D.(5,-2)
2.正方形的边长a与周长之间的函数关系式为=4a,其图象是图中的( )
3.点(3,-5)在正比例函数y=kx(k≠0)的图象上,则k的值为 ( )
A.-15 B.15
4.经过以下一组点可以画出函数y=2x图象的是( )
A.(0,0)和(2,1) B.(1,2)和(-1,-2) C.(1,2)和(2,1) D.(-1,2)和(1,2)
知识点二 正比例函数的性质
5.关于正比例函数 y=-2x,下列结论正确的是( )
A.图象必经过点(-1,-2) B.图象经过第一、三象限
C.y随x的增大而减小 D.不论x取何值,总有 y0
6.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则 m等于( )
A.2 B.-2 C.4 D.-4
7.已知正比例函数y=kx的图象经过点(3,-6).
(1)求这个函数表达式;
(2)画出这个函数图象;
(3)判断点 A(4,-2)、点 B(-1.5,3)是否在这个函数图象上;
(4)图象上的两点 C(x ,y ),D(x ,y ),如果x x ,比较y ,y 的大小.
易错点 求正比例函数关系式时易忽视隐含条件而产生多解
8.已知函数 是正比例函数.
(1)若函数关系式中 y随x的增大而减小,求m的值;
(2)若函数的图象过第一、三象限,求 m的值.
能力提升
9.已知正比例函数 y=kx,当x每增加2时,y减少3,则k的值为( )
10.如图,三个正比例函数的图象分别对应函数关系式:,将a,b,c从小到大排列并用“”连接为( )
11.已知正比例函数y=(2m-1)x的图象上两点A(x ,y ),B(x ,y ),当x
12.将6×6的正方形网格按如图所示的方式放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形 ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形 ABCD 有公共点,则k不可能是( )
A.3 B.2 C.1
13.(1)在同一坐标系内画出正比例函数y =-2x与 的图象.
(2)请你用量角器量一下这两条直线的夹角,你会发现什么 写出你的猜想.
核心拓展
14.如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线,过点(1,0)作x轴的垂线交于点 A ,过点 A 作 y轴的垂线交 于点A ,过点A 作x轴的垂线交 于点A ,过点 A 作y轴的垂线交 于点A ……依次进行下去,则点 A 的坐标为___________,点. 的坐标为______________.
15.已知函数
(1)动手操作:在同一坐标系内画出这四个函数的图象.
(2)探索发现:观察这些函数的图象可以发现,随|k|的增大,直线与 y轴的位置关系有何变化
(3)灵活运用:已知正比例函数y =k x,y =k x在同一坐标系中的图象如图所示,判定k 与k 的大小关系.
参考答案
1. D 2. C
3. D【解析】因为点(3,-5)在正比例函数y=kx(k≠0)的图象上,所以-5=3k,解得 故选 D.
4. B 5. C
6. B【解析】把x=m,y=4代入y=mx中,得m =4,解得m=±2.
因为y的值随x值的增大而减小,所以m=-2.故选 B.
7.解:(1)将点(3,-6)代入y=kx,得-6=3k,解得k=-2.所以函数表达式为y=-2x.
(2)函数图象过点(0,0),(1,-2),描点,连线函数图象如图所示.
(3)将点 A(4,-2)、点 B(-1.5,3)的坐标分别代入表达式,得-2≠-2×4,3=-2×(-1.5).
故点A不在函数图象上,点B在函数图象上.
(4)由于k=-2<0,故y随x的增大而减小,可得y
(2)由题意知m -3=1,且m-1>0.故m=2.
9. C【解析】由当x每增加2时,y减少3,知x每增加1时,y减少 所以k的值为 故选 C.
10. D【解析】根据三个函数图象所在象限可得 a<0,b>0,c>0,再根据直线越陡,|k|越大,则b>c.则b>c>a,即a<c<b.
11. A
12. A 【解析】由图可知,A(1,2),C(2,1),所以当直线y=kx过点A时,k=2;当直线过点C时,2k=1,即 满足 所以k不可能是3.
13.解:(1)如图所示.
(2)两条直线的夹角为90°;当两个一次函数的一次项系数之积为-1时,两条直线的夹角为90°,即两直线垂直.
14.(16,32) (-2 ,-2 )
【解析】当x=1时,y=2,所以点A 的坐标为(1,2);
当y=-x=2时,x=-2,所以点A 的坐标为(-2,2);
同理可得:A (-2,-4),A (4,-4),A (4,8),A (-8,8),A (-8,-16),A (16,-16),
A (16,32),…,所以
,(n为自然数).
因为2027=506×4+3,所以点A 的坐标为
即(-2 0 ,-2 ).
故答案为(16,32);(-2 ,-2 ).
15.解:(1)画图略.
(2)观察函数的图象可以发现,|k|的值越大,直线与y轴的夹角越小.
(3)由(2)中的规律可知,|k |>|k |,且k <0,k <0,所以k <k .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
