第六章 一次函数 培优专题2 一次函数的实际应用的常见类型 同步培优(含解析)
文档属性
| 名称 | 第六章 一次函数 培优专题2 一次函数的实际应用的常见类型 同步培优(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 18:44:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
培优专题2 一次函数的实际应用的常见类型
类型一 由图象获得信息
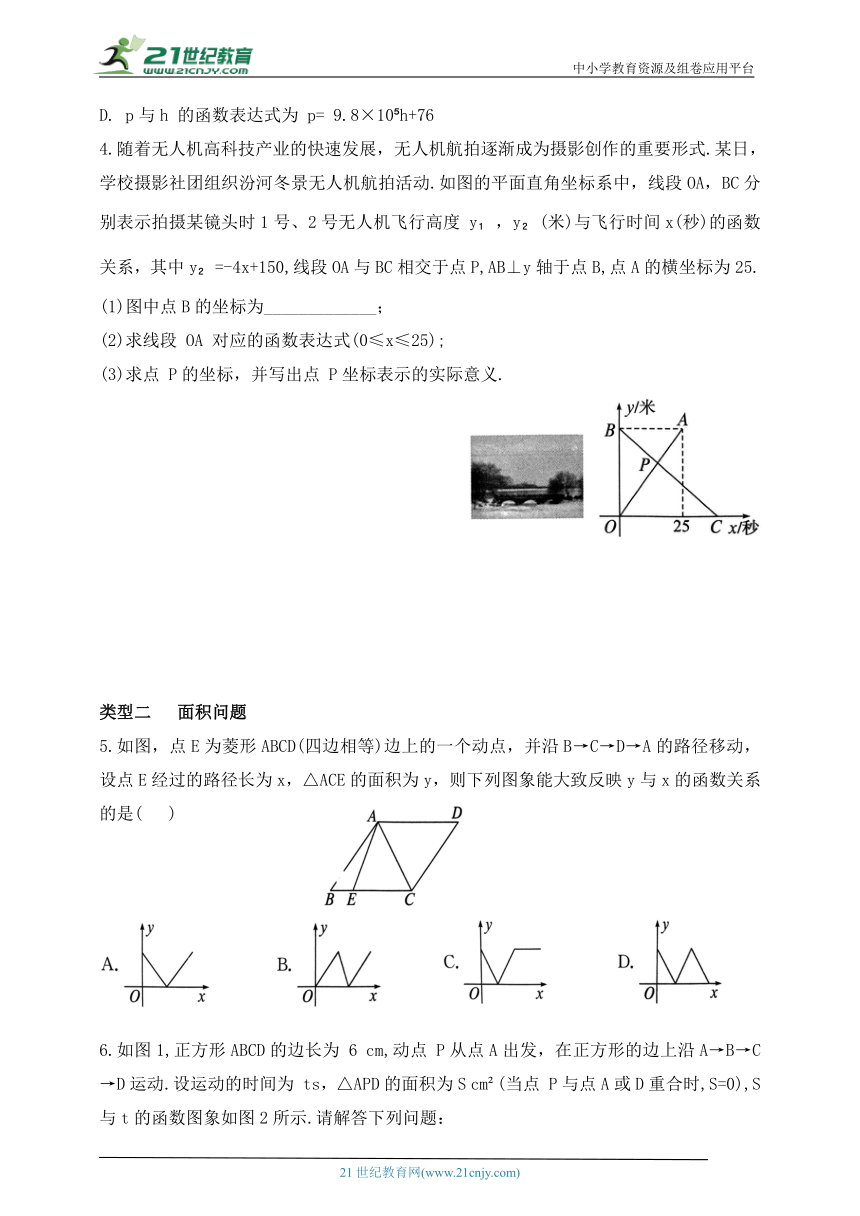
1.甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算,走得最快的是( )
A.甲 B.乙 C.丙 D.丁
2.已知A,B两地相距60km,甲、乙两人沿同一条公路从 A 地出发到B地,甲骑自行车匀速行驶3 h到达,乙骑摩托车,比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15 km B.16 km C.44 km D.45 km
3.如图1是我国青海湖最深处的某一截面图,青海湖水面下任意一点A的压强p(单位:cmHg)与其离水面的深度 h(单位:m)的函数表达式为 p=kh+p ,其图象如图2所示,其中 p。为青海湖水面大气压强,k为常数且k≠0.根据图中信息分析(结果保留一位小数),下列结论正确的是( )
A. 青海湖 水 深 16. 4 m 处的压强为188.6 cmHg
B.青海湖水面大气压强为76.0 cmHg
C.函数表达式p=kh+p 中自变量 h的取值范围是h≥0
D. p与h 的函数表达式为 p= 9.8×10 h+76
4.随着无人机高科技产业的快速发展,无人机航拍逐渐成为摄影创作的重要形式.某日,学校摄影社团组织汾河冬景无人机航拍活动.如图的平面直角坐标系中,线段OA,BC分别表示拍摄某镜头时1号、2号无人机飞行高度 y ,y (米)与飞行时间x(秒)的函数关系,其中y =-4x+150,线段OA与BC相交于点P,AB⊥y轴于点B,点A的横坐标为25.
(1)图中点B的坐标为_____________;
(2)求线段 OA 对应的函数表达式(0≤x≤25);
(3)求点 P的坐标,并写出点 P坐标表示的实际意义.
类型二 面积问题
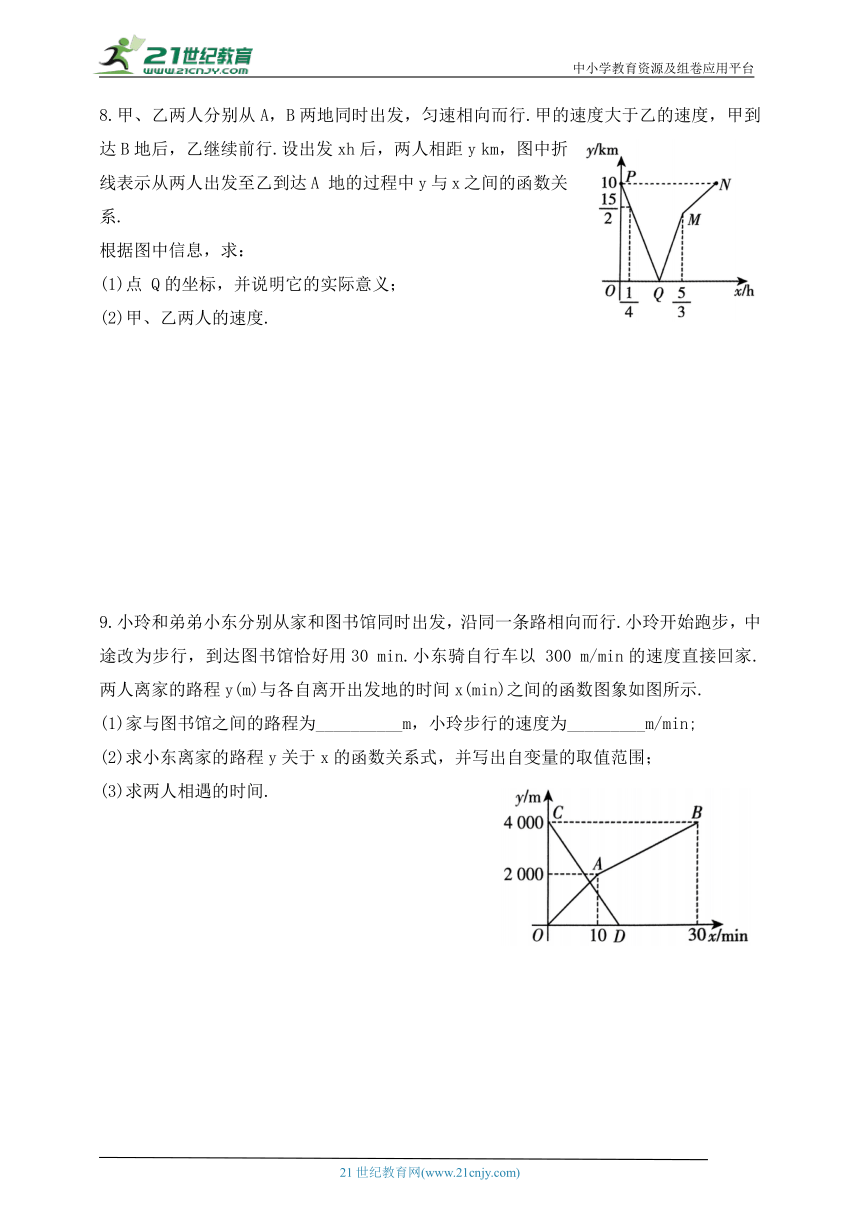
5.如图,点E为菱形ABCD(四边相等)边上的一个动点,并沿B→C→D→A的路径移动,设点E经过的路径长为x,△ACE的面积为y,则下列图象能大致反映y与x的函数关系的是( )
6.如图1,正方形ABCD的边长为 6 cm,动点 P从点A出发,在正方形的边上沿A→B→C→D运动.设运动的时间为 ts,△APD的面积为S cm (当点 P与点A或D重合时,S=0),S与t的函数图象如图2所示.请解答下列问题:
(1)点P在AB 上运动的时间为___________;在CD上运动的速度为_;△APD的面积S的最大值为____________;
(2)求出点P在CD上运动时S与t之间的函数表达式;
(3)当t为何值时,△APD的面积为10cm .
7.如图,在边长为12 cm的正方形 ABCD中,M是AD边的中点,点P从点A出发,在正方形边上沿 A→B→C→D的方向以大于1 cm/s的速度匀速移动,点 Q 从点 D出发,在CD边上沿 D→C方向以1 cm/s的速度匀速移动,P,Q两点同时出发,当点P,Q相遇时即停止移动.设点P移动的时间为t(s),正方形ABCD与∠PMQ的内部重叠部分面积为y(cm ).已知点 P移动到点B 处,y的值为96(即此时正方形ABCD与∠PMQ的内部重叠部分面积为96 cm ).
(1)求点 P的速度;
(2)求 y与t的函数关系式,并直接写出t的取值范围.
类型三 行程问题
8.甲、乙两人分别从A,B两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达B地后,乙继续前行.设出发xh后,两人相距y km,图中折线表示从两人出发至乙到达A 地的过程中y与x之间的函数关系.
根据图中信息,求:
(1)点 Q的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.
9.小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行.小玲开始跑步,中途改为步行,到达图书馆恰好用30 min.小东骑自行车以 300 m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示.
(1)家与图书馆之间的路程为__________m,小玲步行的速度为_________m/min;
(2)求小东离家的路程y关于x的函数关系式,并写出自变量的取值范围;
(3)求两人相遇的时间.
10.小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程 s与时间t的函数关系式;
(2)小明出发多长时间与爸爸第三次相遇
(3)在速度不变的情况下,小明希望比爸爸早20 min 到达公园,则小明在步行过程中停留时间需作怎样调整
类型四 方案优选设计
11.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为 y (元),且y =k x+b(k ≠0);按照方案二所需费用为y (元),且 y =k x(k ≠0).其函数图象如图所示.
(1)求 k 和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k 的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 说明理由.
12.“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需要110 吨和70 吨有机化肥,两个仓库到A,B两个果园的路程如下表所示:
路程/km
甲 乙
A 15 25
B 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元.
(1)根据题意,填写下表:
运量/吨 运费/元
甲 乙 甲 乙
A x 110-x 2×15x 2×25(110-x)
B
(2)设总运费为y元,求y关于x的函数表达式,并求甲仓库运往A果园多少吨有机化肥时,总运费最省 最省的总运费是多少元
参考答案
1. A 【解析】因为30分钟甲比乙步行的路程多,50分钟丁比丙步行的路程多,所以甲的平均速度>乙的平均速度,丁的平均速度>丙的平均速度.
因为步行3千米时,甲比丁用的时间少,所以甲的平均速度>丁的平均速度.所以走的最快的是甲.故选 A.
2. A 【解析】由图象可知:甲的速度为60÷3=20(km/h),乙追上甲时,甲走了 30 km,此时甲所用时间为 30÷20=1.5(h),乙所用时间为1.5-1=0.5(h),所以乙的速度为30÷0.5=60(km/h).
设乙休息半小时再次追上甲时,甲所用时间为t,则20t=60(t-1-0.5),解得t=2.25.
此时甲距离B地为(3-2.25)×20=0.75×20=15(km).
故选 A.
3. A【解析】青海湖水深16.4m处的压强为 4+68=188.6(cmHg),A 项正确.
青海湖水面大气压强为 68.0 cmHg,故B错误.
根据题意知自变量h的取值范围是0≤h≤32.8,故C错误.
p与h的函数表达式中,常数项应为68,故D错误.
4.解:(1)当x=0时,y =-4x+150=150,所以点 B的坐标为(0,150).
(2)由题意知点 A 的坐标为(25,150),设,将(25,150)代入,得150=25x,所以x=6.所以y =6x.
所以线段 OA对应的函数表达式为y =6x(0≤x≤25).
(3)由 解得 所以点P的坐标为(15,90).
点P坐标表示的实际意义是第15秒时1号和2号无人机都在90米的高度.
5. D【解析】当点E在BC 上移动时,△ACE 的面积y随x增大而减小,当点E在CD上移动时,△ACE的面积y随x增大而增大,当点E在DA 上移动时,△ACE的面积y随x增大而减小,且都是一次函数关系.故选D.
6.解:(1)6s 2cm/s 18cm
(2)当点 P在CD上运动时, [6-2(t-12)]=90-6t,即点P在CD上运动时S与t之间的函数表达式为S=90-6t(12≤t≤15).
(3)当0≤t≤6时,易求得S=3t.将S=10代入,得3t=10,解得
当12≤t≤15时,S=90-6t.
将S=10代入,得90-6t=10,解得 所以当t为( 或 时,△APD的面积为10cm .
7.解:(1)因为在边长为12cm的正方形ABCD中,M是AD边的中点, ∠A=∠D=90°,AB=AD=CD=BC=12 cm.
AM=MD=6cm,所以根据题意,得 解得t=4.
因为 所以点P 的速度为3cm/s.
(2)当点P在边AB上时 6t=144-12t(0≤t≤4);
当点 P在边BC 上时, (12-t)=180-21t(4当点P在边CD上时 (8综上所述,y与t的函数关系式为
8.解:(1)设直线 PQ的关系式为y=kx+b,
将点(0,10)和 代入,得解得k=-10,故直线PQ的关系式为y=-10x+10.
当y=0时,x=1.故点 Q的坐标为(1,0).
该点表示甲、乙两人出发后经过1h相遇.
(2)由点M的坐标可知甲经过 h达到B地,故甲的速度为
设乙的速度为x km/h,由两人经过1h相遇,得1·(x+6)=10,解得x=4.
故乙的速度为4k m/h.
9.解:(1)4000 100
(2)因为小东从图书馆到家的时间 所以点D的坐标为
设线段CD的函数关系式为
因为图象过C(0,4 000)和 两点,所以 即b=4 000,k=-300.
所以线段 CD的关系式为y=-300x+4 000.所以小东离家的路程y关于x的函数关系式为
(3)设线段 OA 的函数关系式为 10).
因为图象过点A(10,2 000),所以10k'=2000,解得k'=200.
所以线段 OA的函数关系式为y =200x(0≤x≤10).
当y =y时,有200x=-300x+4000,解得x=8.
故两人出发后 8 min相遇.
10.解:
(2)设小明的爸爸所走的路程s与步行时间t的函数关系式为s=kt+b(k≠0),
则 解得
则小明的爸爸所走的路程与步行时间的关系式为s=30t+250.
当50t-500=30t+250时,解得t=37.5.即t=37.5m in时,小明与爸爸第三次相遇.
(3)30t+250=2500,解得t=75.则小明的爸爸到达公园需要75 min.
因为小明到达公园需要的时间是60 min,小明希望比爸爸早20 min到达公园,所以小明在步行过程中停留的时间需减少5 min.
11.解:(1)因为y =k x+b过点(0,30),(10,180),
所以 解得
k =15表示的实际意义是购买一张学生暑期专享卡后每次健身费用为15元,
b=30表示的实际意义是购买一张学生暑期专享卡的费用为30元.
(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),则k =25×0.8=20.
(3)选择方案一所需费用更少.
理由:由题意可知,y =15x+30,y =20x.
当健身8次时,选择方案一所需费用:y =15×8+30=150(元).
选择方案二所需费用:y =20×8=160(元).
因为150<160,所以选择方案一所需费用更少.
12.解:(1)80-x x-10 2×20(80-x) 2×20(x-10)
(2)y=2×15x+2×25(110-x)+2×20(80-x)+2×20(x-10),即y=-20x+8300(10≤x≤80).
在一次函数y=-20x+8300中,因为-20<0,且10≤x≤80,所以y随x值的增大而减小.
故当x=80时,y最小值为 6700元.
即当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
培优专题2 一次函数的实际应用的常见类型
类型一 由图象获得信息
1.甲、乙、丙、丁四个人步行的路程和所用的时间如图所示,按平均速度计算,走得最快的是( )
A.甲 B.乙 C.丙 D.丁
2.已知A,B两地相距60km,甲、乙两人沿同一条公路从 A 地出发到B地,甲骑自行车匀速行驶3 h到达,乙骑摩托车,比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15 km B.16 km C.44 km D.45 km
3.如图1是我国青海湖最深处的某一截面图,青海湖水面下任意一点A的压强p(单位:cmHg)与其离水面的深度 h(单位:m)的函数表达式为 p=kh+p ,其图象如图2所示,其中 p。为青海湖水面大气压强,k为常数且k≠0.根据图中信息分析(结果保留一位小数),下列结论正确的是( )
A. 青海湖 水 深 16. 4 m 处的压强为188.6 cmHg
B.青海湖水面大气压强为76.0 cmHg
C.函数表达式p=kh+p 中自变量 h的取值范围是h≥0
D. p与h 的函数表达式为 p= 9.8×10 h+76
4.随着无人机高科技产业的快速发展,无人机航拍逐渐成为摄影创作的重要形式.某日,学校摄影社团组织汾河冬景无人机航拍活动.如图的平面直角坐标系中,线段OA,BC分别表示拍摄某镜头时1号、2号无人机飞行高度 y ,y (米)与飞行时间x(秒)的函数关系,其中y =-4x+150,线段OA与BC相交于点P,AB⊥y轴于点B,点A的横坐标为25.
(1)图中点B的坐标为_____________;
(2)求线段 OA 对应的函数表达式(0≤x≤25);
(3)求点 P的坐标,并写出点 P坐标表示的实际意义.
类型二 面积问题
5.如图,点E为菱形ABCD(四边相等)边上的一个动点,并沿B→C→D→A的路径移动,设点E经过的路径长为x,△ACE的面积为y,则下列图象能大致反映y与x的函数关系的是( )
6.如图1,正方形ABCD的边长为 6 cm,动点 P从点A出发,在正方形的边上沿A→B→C→D运动.设运动的时间为 ts,△APD的面积为S cm (当点 P与点A或D重合时,S=0),S与t的函数图象如图2所示.请解答下列问题:
(1)点P在AB 上运动的时间为___________;在CD上运动的速度为_;△APD的面积S的最大值为____________;
(2)求出点P在CD上运动时S与t之间的函数表达式;
(3)当t为何值时,△APD的面积为10cm .
7.如图,在边长为12 cm的正方形 ABCD中,M是AD边的中点,点P从点A出发,在正方形边上沿 A→B→C→D的方向以大于1 cm/s的速度匀速移动,点 Q 从点 D出发,在CD边上沿 D→C方向以1 cm/s的速度匀速移动,P,Q两点同时出发,当点P,Q相遇时即停止移动.设点P移动的时间为t(s),正方形ABCD与∠PMQ的内部重叠部分面积为y(cm ).已知点 P移动到点B 处,y的值为96(即此时正方形ABCD与∠PMQ的内部重叠部分面积为96 cm ).
(1)求点 P的速度;
(2)求 y与t的函数关系式,并直接写出t的取值范围.
类型三 行程问题
8.甲、乙两人分别从A,B两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达B地后,乙继续前行.设出发xh后,两人相距y km,图中折线表示从两人出发至乙到达A 地的过程中y与x之间的函数关系.
根据图中信息,求:
(1)点 Q的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.
9.小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行.小玲开始跑步,中途改为步行,到达图书馆恰好用30 min.小东骑自行车以 300 m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示.
(1)家与图书馆之间的路程为__________m,小玲步行的速度为_________m/min;
(2)求小东离家的路程y关于x的函数关系式,并写出自变量的取值范围;
(3)求两人相遇的时间.
10.小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程 s与时间t的函数关系式;
(2)小明出发多长时间与爸爸第三次相遇
(3)在速度不变的情况下,小明希望比爸爸早20 min 到达公园,则小明在步行过程中停留时间需作怎样调整
类型四 方案优选设计
11.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为 y (元),且y =k x+b(k ≠0);按照方案二所需费用为y (元),且 y =k x(k ≠0).其函数图象如图所示.
(1)求 k 和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k 的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 说明理由.
12.“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需要110 吨和70 吨有机化肥,两个仓库到A,B两个果园的路程如下表所示:
路程/km
甲 乙
A 15 25
B 20 20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元.
(1)根据题意,填写下表:
运量/吨 运费/元
甲 乙 甲 乙
A x 110-x 2×15x 2×25(110-x)
B
(2)设总运费为y元,求y关于x的函数表达式,并求甲仓库运往A果园多少吨有机化肥时,总运费最省 最省的总运费是多少元
参考答案
1. A 【解析】因为30分钟甲比乙步行的路程多,50分钟丁比丙步行的路程多,所以甲的平均速度>乙的平均速度,丁的平均速度>丙的平均速度.
因为步行3千米时,甲比丁用的时间少,所以甲的平均速度>丁的平均速度.所以走的最快的是甲.故选 A.
2. A 【解析】由图象可知:甲的速度为60÷3=20(km/h),乙追上甲时,甲走了 30 km,此时甲所用时间为 30÷20=1.5(h),乙所用时间为1.5-1=0.5(h),所以乙的速度为30÷0.5=60(km/h).
设乙休息半小时再次追上甲时,甲所用时间为t,则20t=60(t-1-0.5),解得t=2.25.
此时甲距离B地为(3-2.25)×20=0.75×20=15(km).
故选 A.
3. A【解析】青海湖水深16.4m处的压强为 4+68=188.6(cmHg),A 项正确.
青海湖水面大气压强为 68.0 cmHg,故B错误.
根据题意知自变量h的取值范围是0≤h≤32.8,故C错误.
p与h的函数表达式中,常数项应为68,故D错误.
4.解:(1)当x=0时,y =-4x+150=150,所以点 B的坐标为(0,150).
(2)由题意知点 A 的坐标为(25,150),设,将(25,150)代入,得150=25x,所以x=6.所以y =6x.
所以线段 OA对应的函数表达式为y =6x(0≤x≤25).
(3)由 解得 所以点P的坐标为(15,90).
点P坐标表示的实际意义是第15秒时1号和2号无人机都在90米的高度.
5. D【解析】当点E在BC 上移动时,△ACE 的面积y随x增大而减小,当点E在CD上移动时,△ACE的面积y随x增大而增大,当点E在DA 上移动时,△ACE的面积y随x增大而减小,且都是一次函数关系.故选D.
6.解:(1)6s 2cm/s 18cm
(2)当点 P在CD上运动时, [6-2(t-12)]=90-6t,即点P在CD上运动时S与t之间的函数表达式为S=90-6t(12≤t≤15).
(3)当0≤t≤6时,易求得S=3t.将S=10代入,得3t=10,解得
当12≤t≤15时,S=90-6t.
将S=10代入,得90-6t=10,解得 所以当t为( 或 时,△APD的面积为10cm .
7.解:(1)因为在边长为12cm的正方形ABCD中,M是AD边的中点, ∠A=∠D=90°,AB=AD=CD=BC=12 cm.
AM=MD=6cm,所以根据题意,得 解得t=4.
因为 所以点P 的速度为3cm/s.
(2)当点P在边AB上时 6t=144-12t(0≤t≤4);
当点 P在边BC 上时, (12-t)=180-21t(4
8.解:(1)设直线 PQ的关系式为y=kx+b,
将点(0,10)和 代入,得解得k=-10,故直线PQ的关系式为y=-10x+10.
当y=0时,x=1.故点 Q的坐标为(1,0).
该点表示甲、乙两人出发后经过1h相遇.
(2)由点M的坐标可知甲经过 h达到B地,故甲的速度为
设乙的速度为x km/h,由两人经过1h相遇,得1·(x+6)=10,解得x=4.
故乙的速度为4k m/h.
9.解:(1)4000 100
(2)因为小东从图书馆到家的时间 所以点D的坐标为
设线段CD的函数关系式为
因为图象过C(0,4 000)和 两点,所以 即b=4 000,k=-300.
所以线段 CD的关系式为y=-300x+4 000.所以小东离家的路程y关于x的函数关系式为
(3)设线段 OA 的函数关系式为 10).
因为图象过点A(10,2 000),所以10k'=2000,解得k'=200.
所以线段 OA的函数关系式为y =200x(0≤x≤10).
当y =y时,有200x=-300x+4000,解得x=8.
故两人出发后 8 min相遇.
10.解:
(2)设小明的爸爸所走的路程s与步行时间t的函数关系式为s=kt+b(k≠0),
则 解得
则小明的爸爸所走的路程与步行时间的关系式为s=30t+250.
当50t-500=30t+250时,解得t=37.5.即t=37.5m in时,小明与爸爸第三次相遇.
(3)30t+250=2500,解得t=75.则小明的爸爸到达公园需要75 min.
因为小明到达公园需要的时间是60 min,小明希望比爸爸早20 min到达公园,所以小明在步行过程中停留的时间需减少5 min.
11.解:(1)因为y =k x+b过点(0,30),(10,180),
所以 解得
k =15表示的实际意义是购买一张学生暑期专享卡后每次健身费用为15元,
b=30表示的实际意义是购买一张学生暑期专享卡的费用为30元.
(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),则k =25×0.8=20.
(3)选择方案一所需费用更少.
理由:由题意可知,y =15x+30,y =20x.
当健身8次时,选择方案一所需费用:y =15×8+30=150(元).
选择方案二所需费用:y =20×8=160(元).
因为150<160,所以选择方案一所需费用更少.
12.解:(1)80-x x-10 2×20(80-x) 2×20(x-10)
(2)y=2×15x+2×25(110-x)+2×20(80-x)+2×20(x-10),即y=-20x+8300(10≤x≤80).
在一次函数y=-20x+8300中,因为-20<0,且10≤x≤80,所以y随x值的增大而减小.
故当x=80时,y最小值为 6700元.
即当甲仓库运往A果园80吨有机化肥时,总运费最省,最省的总运费是6700元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
