第六章 一次函数 章末复习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
章末复习
考点整合
考点1 函数
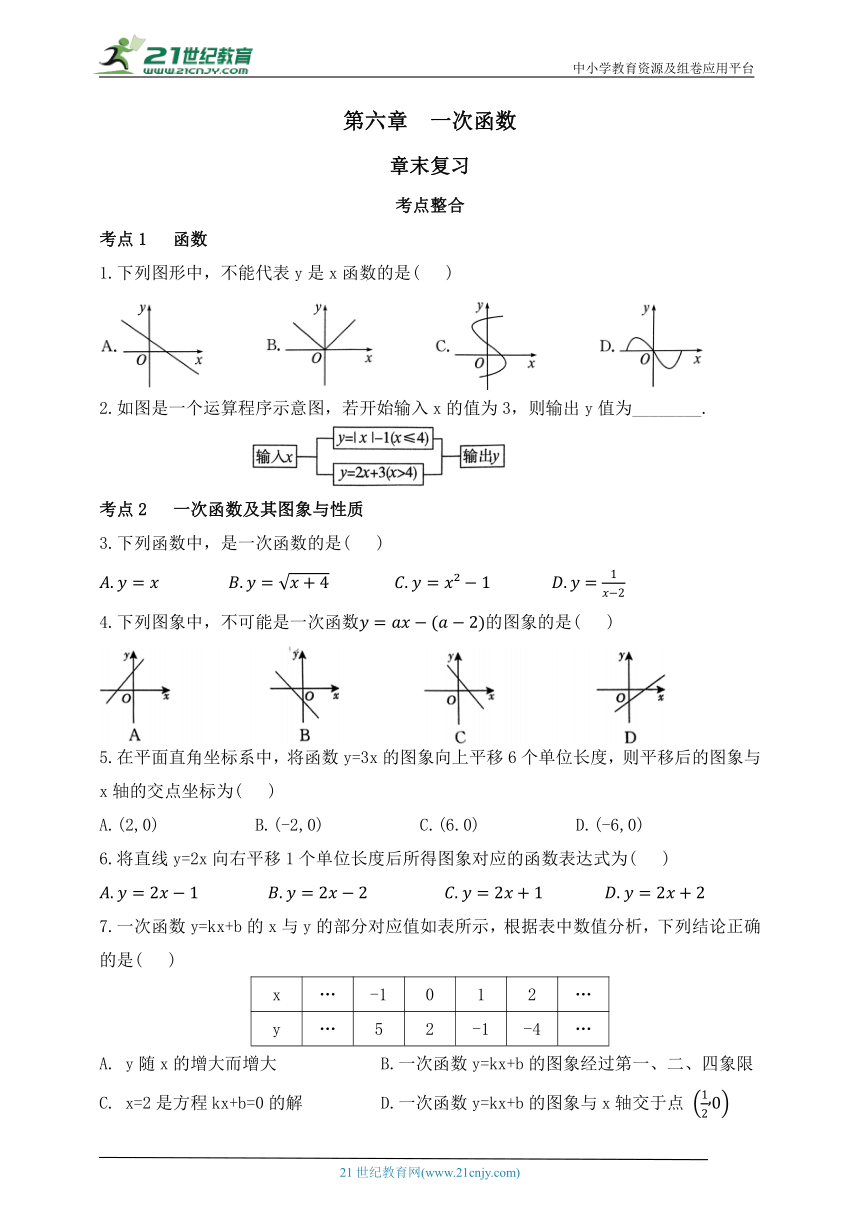
1.下列图形中,不能代表y是x函数的是( )
2.如图是一个运算程序示意图,若开始输入x的值为3,则输出y值为________.
考点2 一次函数及其图象与性质
3.下列函数中,是一次函数的是( )
4.下列图象中,不可能是一次函数的图象的是( )
5.在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与
x轴的交点坐标为( )
A.(2,0) B.(-2,0) C.(6.0) D.(-6,0)
6.将直线y=2x向右平移1个单位长度后所得图象对应的函数表达式为( )
7.一次函数y=kx+b的x与y的部分对应值如表所示,根据表中数值分析,下列结论正确的是( )
x … -1 0 1 2 …
y … 5 2 -1 -4 …
A. y随x的增大而增大 B.一次函数y=kx+b的图象经过第一、二、四象限
C. x=2是方程kx+b=0的解 D.一次函数y=kx+b的图象与x轴交于点
8.一次函数 是关于x的一次函数,则 m,n的值满足的条件为( )
9.如图,在平面直角坐标系 xOy 中,直线与x轴交于点A,直线
与x轴交于点B,且与直线交于点C(-1,m).
(1)求m和b的值;
(2)求△ABC的面积;
(3)若将直线 向下平移t(t>0)个单位长度后,所得到的直线与直线 的交点在第一象限,直接写出t的取值范围.
考点3 一次函数图象的应用
10.甲、乙两辆汽车先后从A地出发到B地,甲车出发1 h后,乙车才出发,如图所示的分别表示甲、乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系.
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系
(2)甲、乙两车的速度分别是多少
(3)试分别确定甲、乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5 h内追上甲车吗 若能,说明理由;若不能,求乙车出发几小时才能追上甲
易错易混
忽略一次函数y=kx+b中k的限制条件而出错
11.已知一次函数 y=ax+|a-1|的图象经过点(0,2),且函数y的值随x的增大而减小,则a的值为___________.
培优创新
12.下列关于一次函数的说法,错误的是 ( )
A.图象经过第一、二、四象限 B. y随x的增大而减小
C.图象与 y轴交于点(0,b) D.当 时,
13.在直线 上,到x轴或y轴的距离为1的点有( )
A.1个 B.2个 C.3个 D.4个
14.把直线y=2x-1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的关系式为_____________.
15.快递公司派甲、乙两车从 A 地将一批物品匀速运往B地,甲出发 0.5时后乙开始出发,结果比甲早1时到达B地,如图,线段OP,MN分别表示甲、乙两车离A 地的距离s(千米)与时间t(时)的关系,a表示A,B两地之间的距离.请结合图中的信息解决如下问题:
(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A 地 并在图中画出甲、乙两车在返回过程中离A 地的距离s(千米)与时间t(时)的图象.
参考答案
1. C【解析】观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.故选C.
2.2 【解析】因为3<4,所以把x=3代入y=|x|-1,得y=3-1=2.故答案为2.
3. A 【解析】A项是正比例函数,也是一次函数;B,D项不是整式函数,不是一次函数;C项不是一次整式,不是一次函数.故选A.
4. B
5. B【解析】将函数y=3x的图象向上平移6个单位长度所得函数的关系式为 y=3x+6.
当y=0时,则3x+6=0,即x=-2,所以平移后的图象与x轴的交点坐标为(-2,0).故选B.
6. B【解析】方法一:y=2x向右平移1个单位长度后所得图象对应的函数表达式为y=2(x-1),即y=2x-2.
方法二:直线y=2x向右平移一个单位长度,经过点(1,0).
设平移后图象的表达式为y=2x+b,将点(1,0)的坐标代入,得0=2+b,得b=-2.所以平移后的图象对应的函数表达式为y=2x-2.故选B.
7. B【解析】由表格可得,y随x的增大而减小,故选项A错误;
当x=0时,y=2,可知b=2,由y随x的增大而减小,可知k<0,则该函数图象经过第一、二、四象限,故选项B正确;
当x=2时,y=-4,故x=2不是方程kx+b=0的解,故选项C错误;
因为点(0,2),(1,-1)在一次函数y=kx+b的图象上,所以 解得 所以y=-3x+2.当y=0时,0=-3x+2,得
即一次函数y=kx+b的图象与x轴交于点 故选项D错误.故选B.
8. A
9.解:(1)把点C(-1,m)的坐标代入 得m=所以点C的坐标为(-1,2).把C(-1,2)的坐标代入y=2x+b,得2=-2+b.解得b=4.
(2)因为直线 与x轴交于点A,直线:与x轴交于点B,所以点A 的坐标为(2,0),点B的坐标为(-2,0).所以AB=4.所以
(3)将直线 l 向下平移t(t>0)个单位长度后,所得到的直线的表达式为 y=2x+4-t.
因为直线 与y轴的交点为 把 的坐标代入y=2x+4-t,得 解得
把A(2,0)代入y=2x+4-t得,4+4-t=0,解得 t=8.所以平移后所得到的直线与直线的交点在第一象限,的取值范围是
10.解:(1)由函数图象得 l 表示乙车离出发地的距离y与追赶时间x之间的关系.
(2)甲车的速度为 乙车的速度为
(3)设甲车的函数关系式为设乙车的函数关系式为y =k x,则k =90,所以y =90x.
(4)不能.设乙车行驶a h可以追上甲车,由题意,得90a=60+60a,解得a=2.
因为1.5<2,所以乙车不能在1.5 h内追上甲车.乙车追上甲车时,乙车行驶了2 h.
11.-1【解析】因为一次函数y=ax+|a-1|的图象过点(0,2),所以|a-1|=2,解得a=3或a=-1.因为y随x的增大而减小,所以a<0,所以a=-1.
12. D【解析】因为 y=kx+b(k<0,b>0),所以图象经过第一、二、四象限,A正确;
因为k<0,所以y随x的增大而减小,B正确;令x=0时,y=b,图象与y轴的交点为(0,b),C正确;令y=0时, 当 时,y<0,D不正确.故选D.
13. C
14. y=2x+3【解析】把直线y=2x-1向左平移1个单位长度,得到y=2(x+1)-1=2x+1,
再向上平移2个单位长度,得到y=2x+3.
15.解:(1)甲的速度为60÷1.5=40(千米/时),乙的速度为 60÷(1.5-0.5)=60(千米/时).
由题意,得 解得a=180.
答:甲、乙两车的速度分别为40千米/时、60千米/时,a的值是180.
(2)甲、乙同时返回A地,则甲返回时所用的时间为 1=2(时),
所以甲返回时的速度为 180÷2=90(千米/时).
图象如图所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
章末复习
考点整合
考点1 函数
1.下列图形中,不能代表y是x函数的是( )
2.如图是一个运算程序示意图,若开始输入x的值为3,则输出y值为________.
考点2 一次函数及其图象与性质
3.下列函数中,是一次函数的是( )
4.下列图象中,不可能是一次函数的图象的是( )
5.在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与
x轴的交点坐标为( )
A.(2,0) B.(-2,0) C.(6.0) D.(-6,0)
6.将直线y=2x向右平移1个单位长度后所得图象对应的函数表达式为( )
7.一次函数y=kx+b的x与y的部分对应值如表所示,根据表中数值分析,下列结论正确的是( )
x … -1 0 1 2 …
y … 5 2 -1 -4 …
A. y随x的增大而增大 B.一次函数y=kx+b的图象经过第一、二、四象限
C. x=2是方程kx+b=0的解 D.一次函数y=kx+b的图象与x轴交于点
8.一次函数 是关于x的一次函数,则 m,n的值满足的条件为( )
9.如图,在平面直角坐标系 xOy 中,直线与x轴交于点A,直线
与x轴交于点B,且与直线交于点C(-1,m).
(1)求m和b的值;
(2)求△ABC的面积;
(3)若将直线 向下平移t(t>0)个单位长度后,所得到的直线与直线 的交点在第一象限,直接写出t的取值范围.
考点3 一次函数图象的应用
10.甲、乙两辆汽车先后从A地出发到B地,甲车出发1 h后,乙车才出发,如图所示的分别表示甲、乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系.
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系
(2)甲、乙两车的速度分别是多少
(3)试分别确定甲、乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5 h内追上甲车吗 若能,说明理由;若不能,求乙车出发几小时才能追上甲
易错易混
忽略一次函数y=kx+b中k的限制条件而出错
11.已知一次函数 y=ax+|a-1|的图象经过点(0,2),且函数y的值随x的增大而减小,则a的值为___________.
培优创新
12.下列关于一次函数的说法,错误的是 ( )
A.图象经过第一、二、四象限 B. y随x的增大而减小
C.图象与 y轴交于点(0,b) D.当 时,
13.在直线 上,到x轴或y轴的距离为1的点有( )
A.1个 B.2个 C.3个 D.4个
14.把直线y=2x-1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的关系式为_____________.
15.快递公司派甲、乙两车从 A 地将一批物品匀速运往B地,甲出发 0.5时后乙开始出发,结果比甲早1时到达B地,如图,线段OP,MN分别表示甲、乙两车离A 地的距离s(千米)与时间t(时)的关系,a表示A,B两地之间的距离.请结合图中的信息解决如下问题:
(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A 地 并在图中画出甲、乙两车在返回过程中离A 地的距离s(千米)与时间t(时)的图象.
参考答案
1. C【解析】观察四个选项,A,B,D三项,对于x的每一个取值,y都有唯一确定的值与之对应;C项中,对于x的每一个取值,y可能有三个值与之对应,不符合函数的定义.故选C.
2.2 【解析】因为3<4,所以把x=3代入y=|x|-1,得y=3-1=2.故答案为2.
3. A 【解析】A项是正比例函数,也是一次函数;B,D项不是整式函数,不是一次函数;C项不是一次整式,不是一次函数.故选A.
4. B
5. B【解析】将函数y=3x的图象向上平移6个单位长度所得函数的关系式为 y=3x+6.
当y=0时,则3x+6=0,即x=-2,所以平移后的图象与x轴的交点坐标为(-2,0).故选B.
6. B【解析】方法一:y=2x向右平移1个单位长度后所得图象对应的函数表达式为y=2(x-1),即y=2x-2.
方法二:直线y=2x向右平移一个单位长度,经过点(1,0).
设平移后图象的表达式为y=2x+b,将点(1,0)的坐标代入,得0=2+b,得b=-2.所以平移后的图象对应的函数表达式为y=2x-2.故选B.
7. B【解析】由表格可得,y随x的增大而减小,故选项A错误;
当x=0时,y=2,可知b=2,由y随x的增大而减小,可知k<0,则该函数图象经过第一、二、四象限,故选项B正确;
当x=2时,y=-4,故x=2不是方程kx+b=0的解,故选项C错误;
因为点(0,2),(1,-1)在一次函数y=kx+b的图象上,所以 解得 所以y=-3x+2.当y=0时,0=-3x+2,得
即一次函数y=kx+b的图象与x轴交于点 故选项D错误.故选B.
8. A
9.解:(1)把点C(-1,m)的坐标代入 得m=所以点C的坐标为(-1,2).把C(-1,2)的坐标代入y=2x+b,得2=-2+b.解得b=4.
(2)因为直线 与x轴交于点A,直线:与x轴交于点B,所以点A 的坐标为(2,0),点B的坐标为(-2,0).所以AB=4.所以
(3)将直线 l 向下平移t(t>0)个单位长度后,所得到的直线的表达式为 y=2x+4-t.
因为直线 与y轴的交点为 把 的坐标代入y=2x+4-t,得 解得
把A(2,0)代入y=2x+4-t得,4+4-t=0,解得 t=8.所以平移后所得到的直线与直线的交点在第一象限,的取值范围是
10.解:(1)由函数图象得 l 表示乙车离出发地的距离y与追赶时间x之间的关系.
(2)甲车的速度为 乙车的速度为
(3)设甲车的函数关系式为设乙车的函数关系式为y =k x,则k =90,所以y =90x.
(4)不能.设乙车行驶a h可以追上甲车,由题意,得90a=60+60a,解得a=2.
因为1.5<2,所以乙车不能在1.5 h内追上甲车.乙车追上甲车时,乙车行驶了2 h.
11.-1【解析】因为一次函数y=ax+|a-1|的图象过点(0,2),所以|a-1|=2,解得a=3或a=-1.因为y随x的增大而减小,所以a<0,所以a=-1.
12. D【解析】因为 y=kx+b(k<0,b>0),所以图象经过第一、二、四象限,A正确;
因为k<0,所以y随x的增大而减小,B正确;令x=0时,y=b,图象与y轴的交点为(0,b),C正确;令y=0时, 当 时,y<0,D不正确.故选D.
13. C
14. y=2x+3【解析】把直线y=2x-1向左平移1个单位长度,得到y=2(x+1)-1=2x+1,
再向上平移2个单位长度,得到y=2x+3.
15.解:(1)甲的速度为60÷1.5=40(千米/时),乙的速度为 60÷(1.5-0.5)=60(千米/时).
由题意,得 解得a=180.
答:甲、乙两车的速度分别为40千米/时、60千米/时,a的值是180.
(2)甲、乙同时返回A地,则甲返回时所用的时间为 1=2(时),
所以甲返回时的速度为 180÷2=90(千米/时).
图象如图所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
