11.2与三角形有关的角 同步训练(含解析) 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 11.2与三角形有关的角 同步训练(含解析) 2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 345.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 22:32:41 | ||
图片预览



文档简介
11.2与三角形有关的角
一、单选题
1.如图,AB∥CD,∠1=30°,∠2=40°,则∠3的度数为( )
A.50° B.60° C.70° D.80°
2.在△ABC中,∠A=60°,∠B=50°,则∠C的度数为()
A.60° B.30° C.70° D.50°
3.如图,在中,,,平分,于点E,则的度数为( )
A. B. C. D.
4.如图,,连接,,,且,下列结论:①若,则;②若与互补,则.则( )
A.仅①正确 B.仅②正确
C.①②都正确 D.①②都不正确
5.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )
A.210° B.110° C.150° D.100°
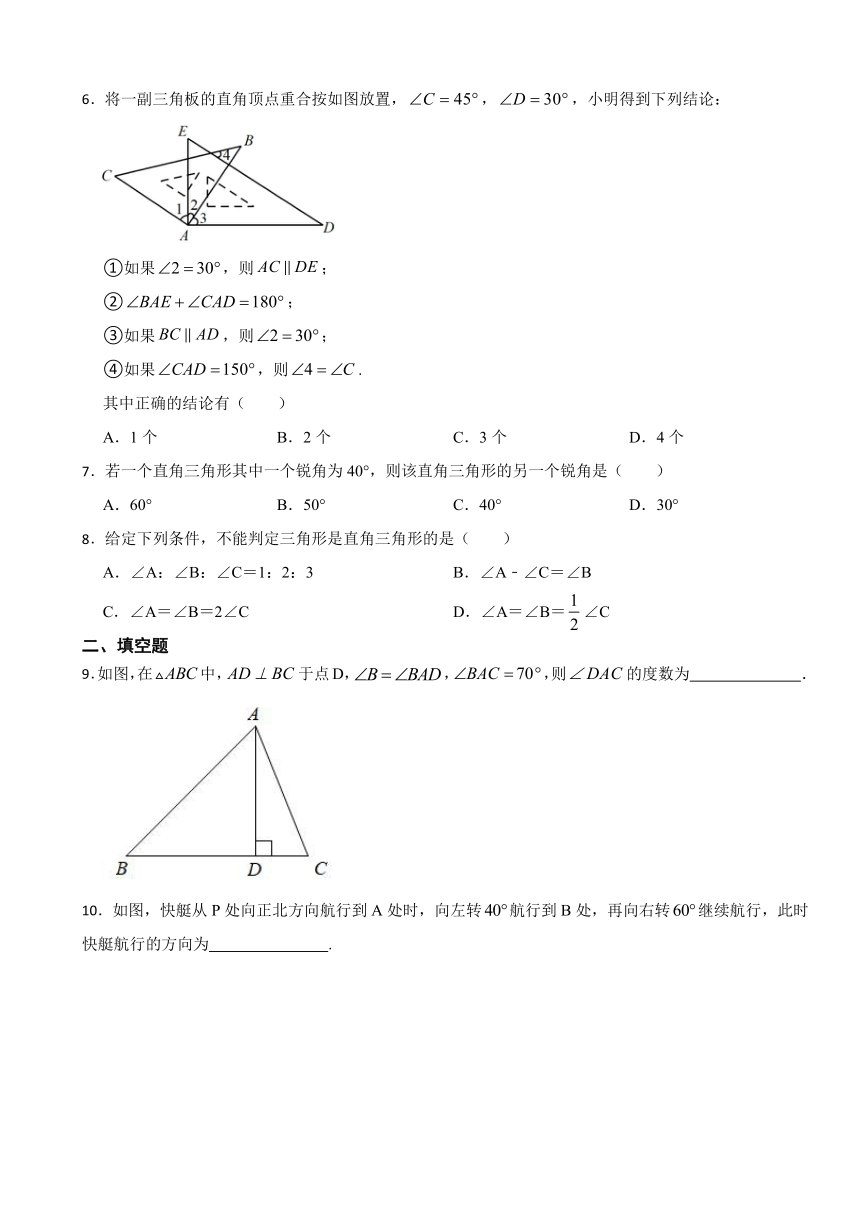
6.将一副三角板的直角顶点重合按如图放置,,,小明得到下列结论:
①如果,则;
②;
③如果,则;
④如果,则.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )
A.60° B.50° C.40° D.30°
8.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C D.∠A=∠B=∠C
二、填空题
9.如图,在中,于点D,,,则的度数为 .
10.如图,快艇从P处向正北方向航行到A处时,向左转航行到B处,再向右转继续航行,此时快艇航行的方向为 .
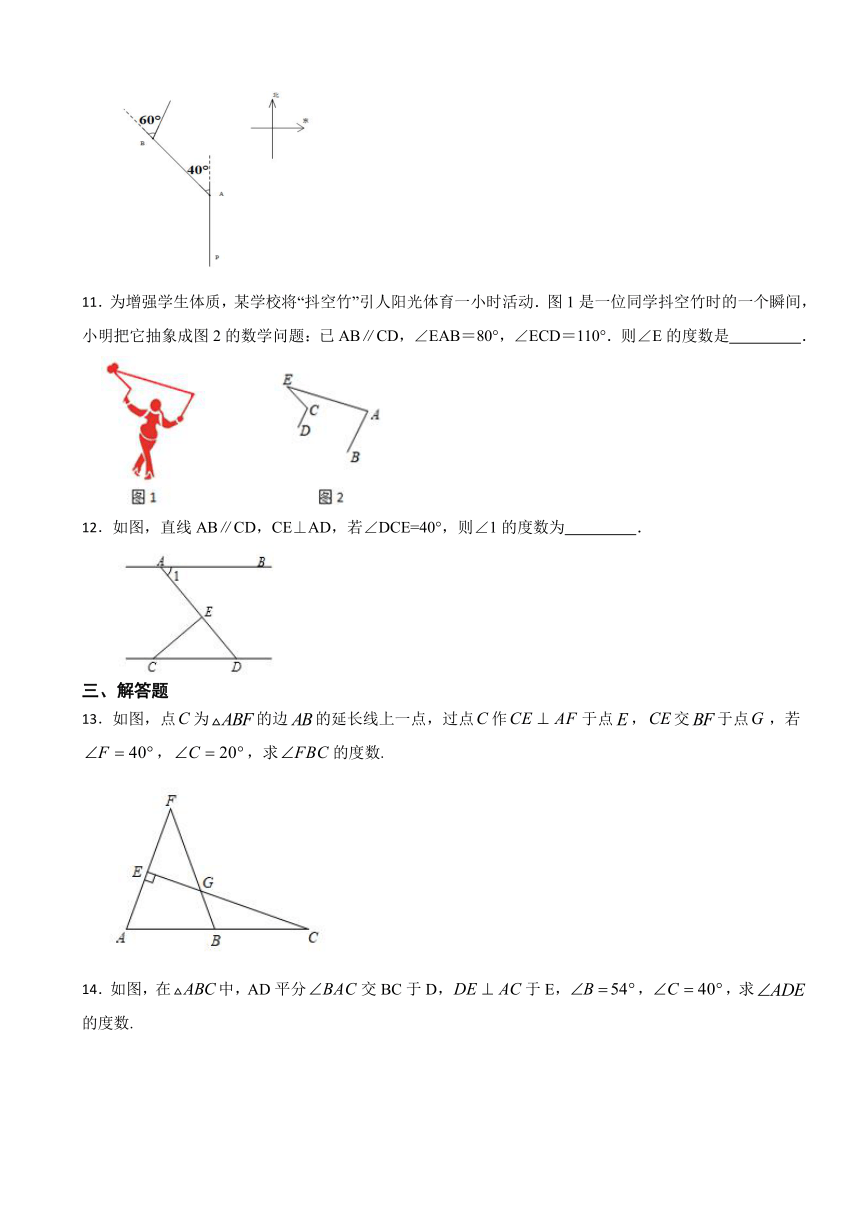
11.为增强学生体质,某学校将“抖空竹”引人阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,小明把它抽象成图2的数学问题:已AB∥CD,∠EAB=80°,∠ECD=110°.则∠E的度数是 .
12.如图,直线AB∥CD,CE⊥AD,若∠DCE=40°,则∠1的度数为 .
三、解答题
13.如图,点为的边的延长线上一点,过点作于点,交于点,若,,求的度数.
14.如图,在中,AD平分交BC于D,于E,,,求的度数.
15.已知:如图,,点E在AC上.求证:.
16.如图,在△ABC中,AD是高,AE、BF是角平分线,且相交于点O,∠ABC=50°,∠C=70°,求∠DAE和∠BOA的度数.
17.如图,在△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,求∠B的度数.
18.如图,在△ABC中,D是BC上一点,AD=BD,∠C=∠ADC,∠BAC=57°,求∠DAC的度数.
19.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=100°,求∠A和∠ACE的度数.
20.填空:
已知:如图,、相交于点.
求证:
证明:∵,( )
∴ .(等式性质)
同理可得:
又∵,( )
∴,(等量代换)
答案解析部分
1.【答案】C
【解析】【解答】解:∵AB∥CD,∠1=30°,
∴∠A=∠1=30°,
又∠2=40°,
∵∠3=∠A+∠2=70°,
故答案为:C.
【分析】根据二直线平行,内错角相等得∠A=∠1=30°,进而再根据三角形外角性质,由∠3=∠A+∠2即可算出答案.
2.【答案】C
【解析】【解答】解:∵ ,
∴ ,
故答案为:C.
【分析】直接根据内角和定理进行计算即可.
3.【答案】C
【解析】【解答】解:∵,
,
,
,
, 平分,
,
.
故答案为:C.
【分析】根据垂直的定义及三角形的内角和定理得∠B=50°,根据角平分线的定义得∠BAD=30°,最后根据三角形外角的性质,由∠ADC=∠B+∠BAD即可算出答案.
4.【答案】C
【解析】【解答】解: ①∵AB∥CD,
∴∠ABC=∠BCD,
∵BD⊥BC,
∴∠BDC=90°-∠BCD,
∴∠A=2∠BDC=180°-2∠BCD,
∠ACB=180°-∠A-∠ABC=180°-(180°-2∠BCD)-∠BCD=∠BCD,故① 正确;
②∵∠A+∠BDC=180°,
∵AB∥CD,
∴∠A+∠ACD=180°,∠ABC=∠BCD,
∴∠BDC=∠ACD=∠ACB+∠BCD=∠ACB+∠ABC,
∵∠BCD+∠BDC=90°,
∴∠ACB+∠ABC+∠BDC=90°,
∴∠ACB+∠ABC+∠ABC=90°,
∴,故 ② 正确.
综上所述, ①② 正确.
故答案为:C.
【分析】根据平行线的性质和三角形内角和定理,结合已知条件把∠ABC和∠ACB分别用∠BCD来表示,即可判断 ① ;根据补角的性质得出∠BDC=∠ACD=∠ACB+∠ABC,结合∠BCD+∠BDC=90°,等量代换即可求出,则可判断②.
5.【答案】A
【解析】【解答】解:∵∠A=30°,
∴∠AMN+∠ANM=180°-∠A=150°
∵∠1+∠AMN=180°,∠2+∠ANM=180°
∴∠1+∠2=180°+180°-(∠AMN+∠ANM)=210°
故答案为:A.
【分析】先求出∠AMN+∠ANM=180°-∠A=150°,再结合∠1+∠AMN=180°,∠2+∠ANM=180°,利用角的运算和等量代换可得∠1+∠2=210°。
6.【答案】C
【解析】【解答】解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
所以其中正确的结论有①②④共3个.
故答案为:C.
【分析】由图形可得∠E=60°,∠2=30°,∠CAB=90°,则∠1=60°,推出∠1=∠E,然后根据平行线的判定定理可判断①;∠BAE+∠CAD=90°-∠1+90°+∠1,据此判断②;根据平行线的性质可得∠3=∠B=45°,然后根据∠2+∠3=∠DAE=90°求出∠2的度数,据此判断③;由②的结论可得∠BAE=30°,根据外角的性质可得∠BOE=∠BAE+∠E=90°,则∠4+∠B=90°,结合∠B的度数求出∠4的度数,进而判断④.
7.【答案】B
【解析】【解答】解:∵直角三角形的一个锐角为40°,
∴另一个锐角为90°-40°=50°.
故答案为:B
【分析】利用直角三角形的两锐角互余,可求出另一个锐角的度数.
8.【答案】C
【解析】【解答】解:A、∵∠A:∠B:∠C=1:2:3,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴∠A+2∠A+3∠A=180°,
∴∠A=30°,
∴∠C=3∠A=90°,
∴△ABC是直角三角形,故A不符合题意;
B、∵∠A+∠B+∠C=180°,∠A-∠C=∠B
∴∠A+∠A-∠C+∠C=180°,
∴∠A=90°,
∴△ABC是直角三角形,故B不符合题意;
C、∵∠A+∠B+∠C=180°,∠A=∠B=2∠C,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,
∴∠A=∠B=72°,
∴△ABC不是直角三角形,故C符合题意;
D、∵∠A+∠B+∠C=180°,∠A=∠B=∠C,
∴∠C+∠C+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故D不 符合题意.
故答案为:C.
【分析】根据题意和三角形内角和定理分别求出△ABC各角的度数,再根据直角三角形的定义进行判断,即可得出答案.
9.【答案】25°/25度
【解析】【解答】解:∵,
∴∠ADB=∠ADC=90°,
又∵,∠B+∠BAD+∠ADB=180°,
∴∠BAD=45°,
∵∠BAC=70°,
∴∠DAC=∠BAC-∠BAD=25°,
故答案为:25°.
【分析】根据垂直先求出∠ADB=∠ADC=90°,再求出∠BAD=45°,最后计算求解即可。
10.【答案】北偏东20°
【解析】【解答】解:如图,根据题意可知∠ABC=180°-60°=120°,
在△ABC中,∠ACB=180°-∠ABC-∠BAC=20°,
∴∠DCE=20°,
∴快艇航行的方向是北偏东20°.
故答案为:北偏东20°.
【分析】画出示意图,根据题意可知∠ABC=180°-60°=120°,利用内角和定理可得∠ACB=20°,由对顶角的性质可得∠DCE=∠ACB=20°,据此解答.
11.【答案】30°
【解析】【解答】解:如图,延长DC交AE于F点,
∵CD∥AB,
∴∠EFC=∠A=80°,
∵∠ECD=110°,∴∠ECF=180°-∠ECD=70°,
∴∠E=180°-∠ECF-∠EFC=180°-70°-80°=30°.
故答案为:30°.
【分析】延长DC交AE于F点,根据平行线的性质求出∠EFC的度数,再根据邻补角的性质求出∠ECF的度数,最后根据三角形内角和定理求∠E度数即可.
12.【答案】50°
【解析】【解答】解:∵CE⊥AD
∴∠CED=90°
∵∠DCE=40°
∴∠EDC=90°-40°=50°
∵AB∥CD
∴∠1=∠EDC=50°
故答案为:50°.
【分析】先利用三角形的内角和求出∠EDC=90°-40°=50°,再利用平行线的性质可得∠1=∠EDC=50°。
13.【答案】解:∵在中,,
∴,
∴,
∴.
【解析】【分析】根据垂直的定义得∠AEC=90°,根据直角三角形两锐角互余得∠A=70°,进而根据三角形外角性质得∠FBC=∠A+∠F,代入计算即可得出答案.
14.【答案】解:∵ , ,
∴ .
∵ 平分 ,
∴ .
∵ ,
∴
∴.
【解析】【分析】首先根据三角形的内角和定理算出∠BAC的度数,再根据角平分线的定义算出∠DAE的度数,由垂直定义得∠AED=90°,最后再根据三角形内角和定理即可算出答案.
15.【答案】证明:在 中,
∵(三角形内角和定理),
∴(等式的性质),
又∵(已知),
∴(两直线平行,同旁内角互补),
∴(等式的性质),
∴(等量代换).
【解析】【分析】在三角形CED中,根据三角形内角和定理可将∠CED+∠D用含∠C的代数式表示出来,然后由两直线平行同旁内角互补可得∠A+∠C=180°,于是∠A也可用含∠C的代数式表示出来,根据表示的代数式即可判断求解.
16.【答案】解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°,
∵∠ABC=50°,
∴∠BAC=180°﹣∠ABC﹣∠C=60°,
∵AE是∠BAC的角平分线,
∴∠EAC=∠BAE=30°,
∴∠EAD=∠EAC﹣∠CAD=30°﹣20°=10°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°,
故∠DAE和∠BOA的度数分别是10°和125°.
【解析】【分析】先利用垂直的定义得出∠ADC=90°,接着利用三角形内角和定理得出∠CAD、∠BAC,再利用角平分线的性质和三角形内角和定理即可求解。
17.【答案】解:∵,
∴,.
设,
∴.
∵,
∴,
在中,
∵,
∴,
∴,
∴.
【解析】【分析】设,则,再结合,可得,求出,即可得到。
18.【答案】解:∵AD=BD,
∴∠B=∠BAD,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠C=2∠B,
∵∠BAC=57°,
∴∠B+∠C=3∠B=180°-∠BAC=41°,
∴∠ADC=∠C=82°,
∴∠DAC=16°.
【解析】【分析】由三角形内角和定理和角的运算即可得解。
19.【答案】解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB﹣∠ACB=100°﹣60°=40°.
∵BD是角平分线,
∴∠ABC=80°,
∴∠A=180°﹣∠ABC﹣∠ACB=40°;
∵CE是高,
∴∠AEC=90°,
∴∠ACE=90°﹣∠A=50°
【解析】【分析】根据题意先求出 ∠DBC=∠ADB﹣∠ACB=100°﹣60°=40°,再根据角平分线求出∠ABC=80°, 最后计算求解即可。
20.【答案】证明:∵,(三角形的内角和等于180°)
∴.(等式性质)
同理可得:
又∵,(对顶角相等)
∴,(等量代换)
故答案为:三角形的内角和等于180°, 1, 2, 对顶角相等
【解析】【分析】由三角形的内角和等量得∠A+∠B+∠1=180°, 根据等式的性质得∠A+∠B=180°-∠1 ,同理得出∠C+∠D=180°-∠2 ,根据对顶角的性质得出∠1=∠2,再等量代换,即可得出结论.
一、单选题
1.如图,AB∥CD,∠1=30°,∠2=40°,则∠3的度数为( )
A.50° B.60° C.70° D.80°
2.在△ABC中,∠A=60°,∠B=50°,则∠C的度数为()
A.60° B.30° C.70° D.50°
3.如图,在中,,,平分,于点E,则的度数为( )
A. B. C. D.
4.如图,,连接,,,且,下列结论:①若,则;②若与互补,则.则( )
A.仅①正确 B.仅②正确
C.①②都正确 D.①②都不正确
5.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )
A.210° B.110° C.150° D.100°
6.将一副三角板的直角顶点重合按如图放置,,,小明得到下列结论:
①如果,则;
②;
③如果,则;
④如果,则.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )
A.60° B.50° C.40° D.30°
8.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C D.∠A=∠B=∠C
二、填空题
9.如图,在中,于点D,,,则的度数为 .
10.如图,快艇从P处向正北方向航行到A处时,向左转航行到B处,再向右转继续航行,此时快艇航行的方向为 .
11.为增强学生体质,某学校将“抖空竹”引人阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,小明把它抽象成图2的数学问题:已AB∥CD,∠EAB=80°,∠ECD=110°.则∠E的度数是 .
12.如图,直线AB∥CD,CE⊥AD,若∠DCE=40°,则∠1的度数为 .
三、解答题
13.如图,点为的边的延长线上一点,过点作于点,交于点,若,,求的度数.
14.如图,在中,AD平分交BC于D,于E,,,求的度数.
15.已知:如图,,点E在AC上.求证:.
16.如图,在△ABC中,AD是高,AE、BF是角平分线,且相交于点O,∠ABC=50°,∠C=70°,求∠DAE和∠BOA的度数.
17.如图,在△ABC中,D是BC上一点,AC=AD=DB,∠BAC=105°,求∠B的度数.
18.如图,在△ABC中,D是BC上一点,AD=BD,∠C=∠ADC,∠BAC=57°,求∠DAC的度数.
19.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=100°,求∠A和∠ACE的度数.
20.填空:
已知:如图,、相交于点.
求证:
证明:∵,( )
∴ .(等式性质)
同理可得:
又∵,( )
∴,(等量代换)
答案解析部分
1.【答案】C
【解析】【解答】解:∵AB∥CD,∠1=30°,
∴∠A=∠1=30°,
又∠2=40°,
∵∠3=∠A+∠2=70°,
故答案为:C.
【分析】根据二直线平行,内错角相等得∠A=∠1=30°,进而再根据三角形外角性质,由∠3=∠A+∠2即可算出答案.
2.【答案】C
【解析】【解答】解:∵ ,
∴ ,
故答案为:C.
【分析】直接根据内角和定理进行计算即可.
3.【答案】C
【解析】【解答】解:∵,
,
,
,
, 平分,
,
.
故答案为:C.
【分析】根据垂直的定义及三角形的内角和定理得∠B=50°,根据角平分线的定义得∠BAD=30°,最后根据三角形外角的性质,由∠ADC=∠B+∠BAD即可算出答案.
4.【答案】C
【解析】【解答】解: ①∵AB∥CD,
∴∠ABC=∠BCD,
∵BD⊥BC,
∴∠BDC=90°-∠BCD,
∴∠A=2∠BDC=180°-2∠BCD,
∠ACB=180°-∠A-∠ABC=180°-(180°-2∠BCD)-∠BCD=∠BCD,故① 正确;
②∵∠A+∠BDC=180°,
∵AB∥CD,
∴∠A+∠ACD=180°,∠ABC=∠BCD,
∴∠BDC=∠ACD=∠ACB+∠BCD=∠ACB+∠ABC,
∵∠BCD+∠BDC=90°,
∴∠ACB+∠ABC+∠BDC=90°,
∴∠ACB+∠ABC+∠ABC=90°,
∴,故 ② 正确.
综上所述, ①② 正确.
故答案为:C.
【分析】根据平行线的性质和三角形内角和定理,结合已知条件把∠ABC和∠ACB分别用∠BCD来表示,即可判断 ① ;根据补角的性质得出∠BDC=∠ACD=∠ACB+∠ABC,结合∠BCD+∠BDC=90°,等量代换即可求出,则可判断②.
5.【答案】A
【解析】【解答】解:∵∠A=30°,
∴∠AMN+∠ANM=180°-∠A=150°
∵∠1+∠AMN=180°,∠2+∠ANM=180°
∴∠1+∠2=180°+180°-(∠AMN+∠ANM)=210°
故答案为:A.
【分析】先求出∠AMN+∠ANM=180°-∠A=150°,再结合∠1+∠AMN=180°,∠2+∠ANM=180°,利用角的运算和等量代换可得∠1+∠2=210°。
6.【答案】C
【解析】【解答】解:∵∠2=30°,∠CAB=90°,
∴∠1=60°,
∵∠E=60°,
∴∠1=∠E,
∴,故①正确;
∵∠CAB=∠DAE=90°,
∴∠BAE+∠CAD=90°﹣∠1+90°+∠1=180°,故②正确;
∵,∠B=45°,
∴∠3=∠B=45°,
∵∠2+∠3=∠DAE=90°,
∴∠2=45°,故③错误;
∵∠CAD=150°,∠BAE+∠CAD=180°,
∴∠BAE=30°,
∵∠E=60°,
∴∠BOE=∠BAE+∠E=90°,
∴∠4+∠B=90°,
∵∠B=45°,
∴∠4=45°,
∵∠C=45°,
∴∠4=∠C,故④正确;
所以其中正确的结论有①②④共3个.
故答案为:C.
【分析】由图形可得∠E=60°,∠2=30°,∠CAB=90°,则∠1=60°,推出∠1=∠E,然后根据平行线的判定定理可判断①;∠BAE+∠CAD=90°-∠1+90°+∠1,据此判断②;根据平行线的性质可得∠3=∠B=45°,然后根据∠2+∠3=∠DAE=90°求出∠2的度数,据此判断③;由②的结论可得∠BAE=30°,根据外角的性质可得∠BOE=∠BAE+∠E=90°,则∠4+∠B=90°,结合∠B的度数求出∠4的度数,进而判断④.
7.【答案】B
【解析】【解答】解:∵直角三角形的一个锐角为40°,
∴另一个锐角为90°-40°=50°.
故答案为:B
【分析】利用直角三角形的两锐角互余,可求出另一个锐角的度数.
8.【答案】C
【解析】【解答】解:A、∵∠A:∠B:∠C=1:2:3,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,
∴∠A+2∠A+3∠A=180°,
∴∠A=30°,
∴∠C=3∠A=90°,
∴△ABC是直角三角形,故A不符合题意;
B、∵∠A+∠B+∠C=180°,∠A-∠C=∠B
∴∠A+∠A-∠C+∠C=180°,
∴∠A=90°,
∴△ABC是直角三角形,故B不符合题意;
C、∵∠A+∠B+∠C=180°,∠A=∠B=2∠C,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,
∴∠A=∠B=72°,
∴△ABC不是直角三角形,故C符合题意;
D、∵∠A+∠B+∠C=180°,∠A=∠B=∠C,
∴∠C+∠C+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故D不 符合题意.
故答案为:C.
【分析】根据题意和三角形内角和定理分别求出△ABC各角的度数,再根据直角三角形的定义进行判断,即可得出答案.
9.【答案】25°/25度
【解析】【解答】解:∵,
∴∠ADB=∠ADC=90°,
又∵,∠B+∠BAD+∠ADB=180°,
∴∠BAD=45°,
∵∠BAC=70°,
∴∠DAC=∠BAC-∠BAD=25°,
故答案为:25°.
【分析】根据垂直先求出∠ADB=∠ADC=90°,再求出∠BAD=45°,最后计算求解即可。
10.【答案】北偏东20°
【解析】【解答】解:如图,根据题意可知∠ABC=180°-60°=120°,
在△ABC中,∠ACB=180°-∠ABC-∠BAC=20°,
∴∠DCE=20°,
∴快艇航行的方向是北偏东20°.
故答案为:北偏东20°.
【分析】画出示意图,根据题意可知∠ABC=180°-60°=120°,利用内角和定理可得∠ACB=20°,由对顶角的性质可得∠DCE=∠ACB=20°,据此解答.
11.【答案】30°
【解析】【解答】解:如图,延长DC交AE于F点,
∵CD∥AB,
∴∠EFC=∠A=80°,
∵∠ECD=110°,∴∠ECF=180°-∠ECD=70°,
∴∠E=180°-∠ECF-∠EFC=180°-70°-80°=30°.
故答案为:30°.
【分析】延长DC交AE于F点,根据平行线的性质求出∠EFC的度数,再根据邻补角的性质求出∠ECF的度数,最后根据三角形内角和定理求∠E度数即可.
12.【答案】50°
【解析】【解答】解:∵CE⊥AD
∴∠CED=90°
∵∠DCE=40°
∴∠EDC=90°-40°=50°
∵AB∥CD
∴∠1=∠EDC=50°
故答案为:50°.
【分析】先利用三角形的内角和求出∠EDC=90°-40°=50°,再利用平行线的性质可得∠1=∠EDC=50°。
13.【答案】解:∵在中,,
∴,
∴,
∴.
【解析】【分析】根据垂直的定义得∠AEC=90°,根据直角三角形两锐角互余得∠A=70°,进而根据三角形外角性质得∠FBC=∠A+∠F,代入计算即可得出答案.
14.【答案】解:∵ , ,
∴ .
∵ 平分 ,
∴ .
∵ ,
∴
∴.
【解析】【分析】首先根据三角形的内角和定理算出∠BAC的度数,再根据角平分线的定义算出∠DAE的度数,由垂直定义得∠AED=90°,最后再根据三角形内角和定理即可算出答案.
15.【答案】证明:在 中,
∵(三角形内角和定理),
∴(等式的性质),
又∵(已知),
∴(两直线平行,同旁内角互补),
∴(等式的性质),
∴(等量代换).
【解析】【分析】在三角形CED中,根据三角形内角和定理可将∠CED+∠D用含∠C的代数式表示出来,然后由两直线平行同旁内角互补可得∠A+∠C=180°,于是∠A也可用含∠C的代数式表示出来,根据表示的代数式即可判断求解.
16.【答案】解:∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°,
∵∠ABC=50°,
∴∠BAC=180°﹣∠ABC﹣∠C=60°,
∵AE是∠BAC的角平分线,
∴∠EAC=∠BAE=30°,
∴∠EAD=∠EAC﹣∠CAD=30°﹣20°=10°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣30°﹣25°=125°,
故∠DAE和∠BOA的度数分别是10°和125°.
【解析】【分析】先利用垂直的定义得出∠ADC=90°,接着利用三角形内角和定理得出∠CAD、∠BAC,再利用角平分线的性质和三角形内角和定理即可求解。
17.【答案】解:∵,
∴,.
设,
∴.
∵,
∴,
在中,
∵,
∴,
∴,
∴.
【解析】【分析】设,则,再结合,可得,求出,即可得到。
18.【答案】解:∵AD=BD,
∴∠B=∠BAD,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠C=2∠B,
∵∠BAC=57°,
∴∠B+∠C=3∠B=180°-∠BAC=41°,
∴∠ADC=∠C=82°,
∴∠DAC=16°.
【解析】【分析】由三角形内角和定理和角的运算即可得解。
19.【答案】解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB﹣∠ACB=100°﹣60°=40°.
∵BD是角平分线,
∴∠ABC=80°,
∴∠A=180°﹣∠ABC﹣∠ACB=40°;
∵CE是高,
∴∠AEC=90°,
∴∠ACE=90°﹣∠A=50°
【解析】【分析】根据题意先求出 ∠DBC=∠ADB﹣∠ACB=100°﹣60°=40°,再根据角平分线求出∠ABC=80°, 最后计算求解即可。
20.【答案】证明:∵,(三角形的内角和等于180°)
∴.(等式性质)
同理可得:
又∵,(对顶角相等)
∴,(等量代换)
故答案为:三角形的内角和等于180°, 1, 2, 对顶角相等
【解析】【分析】由三角形的内角和等量得∠A+∠B+∠1=180°, 根据等式的性质得∠A+∠B=180°-∠1 ,同理得出∠C+∠D=180°-∠2 ,根据对顶角的性质得出∠1=∠2,再等量代换,即可得出结论.
