2023-2024学年人教版九年级数学上册23.1.1 旋转的概念及性质 练习题 (含答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册23.1.1 旋转的概念及性质 练习题 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 281.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 22:42:54 | ||
图片预览



文档简介
23.1.1 旋转的概念及性质
一、单项选择题
1.下列运动中,不属于旋转变换的是( )
A.钟摆的运动 B.行驶中的汽车车轮 C.电梯的升降运动 D.方向盘的转动
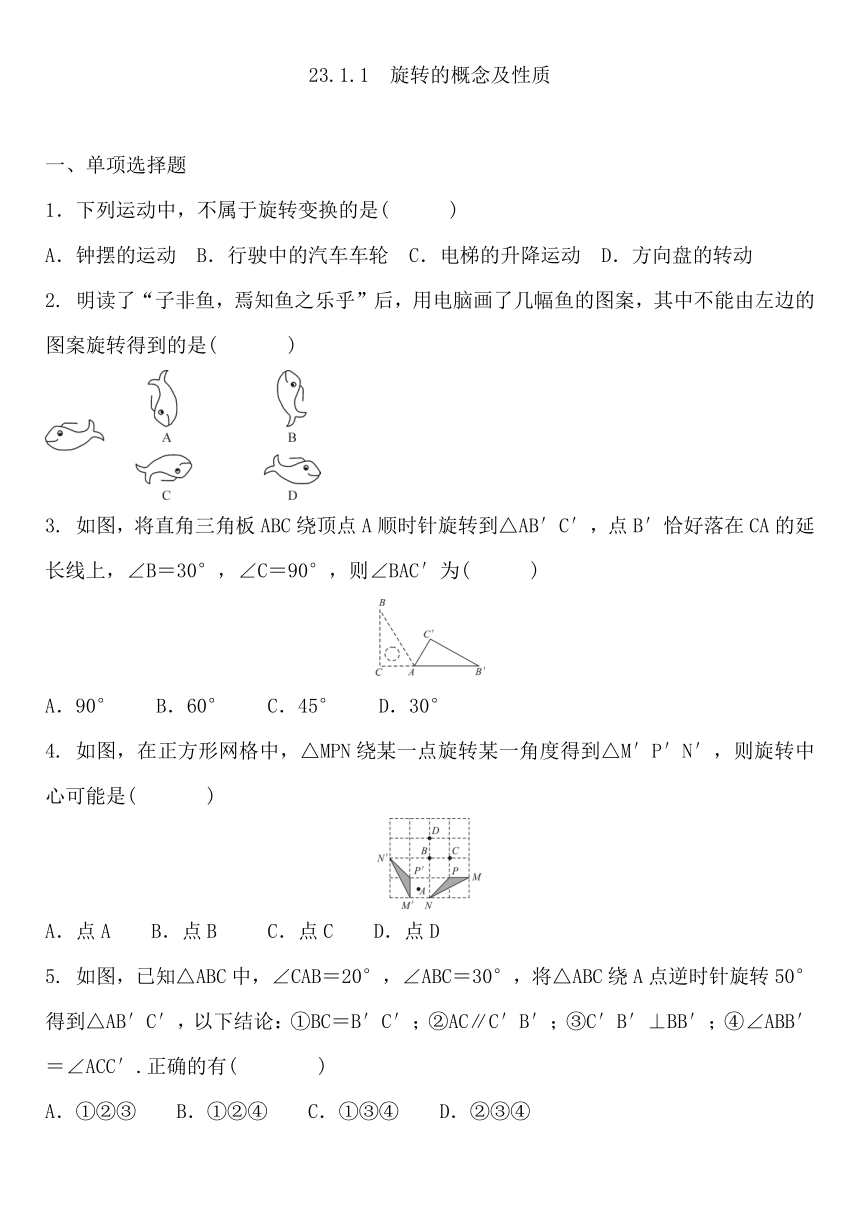
2. 明读了“子非鱼,焉知鱼之乐乎”后,用电脑画了几幅鱼的图案,其中不能由左边的图案旋转得到的是( )
3. 如图,将直角三角板ABC绕顶点A顺时针旋转到△AB′C′,点B′恰好落在CA的延长线上,∠B=30°,∠C=90°,则∠BAC′为( )
A.90° B.60° C.45° D.30°
4. 如图,在正方形网格中,△MPN绕某一点旋转某一角度得到△M′P′N′,则旋转中心可能是( )
A.点A B.点B C.点C D.点D
5. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′;②AC∥C′B′;③C′B′⊥BB′;④∠ABB′=∠ACC′.正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
6. 如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )
A.AB=AN B.AB∥NC C.∠AMN=∠ACN D.MN⊥AC
二、填空题
7. 如图,已知△AOB绕点O旋转至△A′OB′,则:
(1)点B的对应点是 _______;
(2)旋转中心是 ______,旋转角为 ____________;
(3)∠A的对应角是 _______,线段OB的对应线段是线段 ______.
8. 如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为 _____.
9. 下列图案中能由一个图形通过旋转而构成的是 _______.(填序号)
10. 如图,在△ABC中,∠ACB=74°,将△ABC在平面内绕点A旋转50°到△AB′C′的位置,连接CC′,则∠CC′B′的度数为 ______.
三、解答题
11. 如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连接CE,绕点C顺时针旋转110°,得到线段CF,连接BE,DF.若∠E=86°,求∠F的度数.
12. 如图,在△ABC中,点D在AB边上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE与AC交于点F,且∠B=70°,∠A=10°.
(1)求证:AB=ED;
(2)求∠AFE的度数.
13. 如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.
(1)如图①,当A,C,D三点在同一直线上时,∠AFB的度数为60°,线段AE与BD的数量关系为AE=BD;
(2)如图②,当△ECD绕点C顺时针旋转α(0°≤α<360°)时,(1)中的结论是否还成立?若不成立,请说明理由;若成立,请就图②给予证明;
(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.
答案:
一、
1-6 CDBBB C
二、
7. (1) 点B′
(2) 点O AOA′或∠BOB′
(3) ∠A′ OB′
8.
9. ①②
10. 9°
三、
11. 解:∵四边形ABCD是菱形,∴BC=CD,∠BCD=∠A=110°.
由旋转的性质知,CE=CF,∵∠ECF=∠BCD=110°,∴∠BCE=∠DCF.
在△BCE和△DCF中,∴△BCE≌△DCF.∴∠F=∠E=86°
12. 解:(1)∵∠ECA=∠DCB,∴∠ECA+∠ACD=∠DCB+∠ACD,即∠DCE=∠BCA,
由旋转可得CA=CE,又∵CB=CD,∴△BCA≌△DCE(SAS).∴AB=ED
(2)由(1)中结论可得∠CDE=∠B=70°,又∵CB=CD,∴∠B=∠CDB=70°,
∴∠EDA=180°-∠BDE=180°-70°×2=40°,
∴∠AFE=∠EDA+∠A=40°+10°=50°
13. 解:(2)(1)中结论仍成立.
证明:∵△ABC是等边三角形,∴AC=BC,∠ACB=60°.又∵△ECD是等边三角形,∴CE=CD,∠DCE=60°,∴∠ACB=∠DCE=60°,∴∠ACB+∠1=∠DCE+∠1,即∠ACE=∠BCD.
易证△ACE≌△BCD,∴AE=BD,∠2=∠3.
∵∠AFB+∠3=∠ACB+∠2,且∠ACB=60°,∴∠AFB=60°
(3)∵△ABC是等边三角形,∴AC=BC=4,
当旋转60°时,B,C,D三点共线,此时BD最大,最大为BC+CD=7;当旋转240°时,B,C,D三点共线,此时BD最小,最小为BC-CD=1,∴1≤BD≤7
一、单项选择题
1.下列运动中,不属于旋转变换的是( )
A.钟摆的运动 B.行驶中的汽车车轮 C.电梯的升降运动 D.方向盘的转动
2. 明读了“子非鱼,焉知鱼之乐乎”后,用电脑画了几幅鱼的图案,其中不能由左边的图案旋转得到的是( )
3. 如图,将直角三角板ABC绕顶点A顺时针旋转到△AB′C′,点B′恰好落在CA的延长线上,∠B=30°,∠C=90°,则∠BAC′为( )
A.90° B.60° C.45° D.30°
4. 如图,在正方形网格中,△MPN绕某一点旋转某一角度得到△M′P′N′,则旋转中心可能是( )
A.点A B.点B C.点C D.点D
5. 如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,以下结论:①BC=B′C′;②AC∥C′B′;③C′B′⊥BB′;④∠ABB′=∠ACC′.正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
6. 如图,在△ABC中,AB=AC,若M是BC边上任意一点,将△ABM绕点A逆时针旋转得到△ACN,点M的对应点为点N,连接MN,则下列结论一定正确的是( )
A.AB=AN B.AB∥NC C.∠AMN=∠ACN D.MN⊥AC
二、填空题
7. 如图,已知△AOB绕点O旋转至△A′OB′,则:
(1)点B的对应点是 _______;
(2)旋转中心是 ______,旋转角为 ____________;
(3)∠A的对应角是 _______,线段OB的对应线段是线段 ______.
8. 如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为 _____.
9. 下列图案中能由一个图形通过旋转而构成的是 _______.(填序号)
10. 如图,在△ABC中,∠ACB=74°,将△ABC在平面内绕点A旋转50°到△AB′C′的位置,连接CC′,则∠CC′B′的度数为 ______.
三、解答题
11. 如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连接CE,绕点C顺时针旋转110°,得到线段CF,连接BE,DF.若∠E=86°,求∠F的度数.
12. 如图,在△ABC中,点D在AB边上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE与AC交于点F,且∠B=70°,∠A=10°.
(1)求证:AB=ED;
(2)求∠AFE的度数.
13. 如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.
(1)如图①,当A,C,D三点在同一直线上时,∠AFB的度数为60°,线段AE与BD的数量关系为AE=BD;
(2)如图②,当△ECD绕点C顺时针旋转α(0°≤α<360°)时,(1)中的结论是否还成立?若不成立,请说明理由;若成立,请就图②给予证明;
(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.
答案:
一、
1-6 CDBBB C
二、
7. (1) 点B′
(2) 点O AOA′或∠BOB′
(3) ∠A′ OB′
8.
9. ①②
10. 9°
三、
11. 解:∵四边形ABCD是菱形,∴BC=CD,∠BCD=∠A=110°.
由旋转的性质知,CE=CF,∵∠ECF=∠BCD=110°,∴∠BCE=∠DCF.
在△BCE和△DCF中,∴△BCE≌△DCF.∴∠F=∠E=86°
12. 解:(1)∵∠ECA=∠DCB,∴∠ECA+∠ACD=∠DCB+∠ACD,即∠DCE=∠BCA,
由旋转可得CA=CE,又∵CB=CD,∴△BCA≌△DCE(SAS).∴AB=ED
(2)由(1)中结论可得∠CDE=∠B=70°,又∵CB=CD,∴∠B=∠CDB=70°,
∴∠EDA=180°-∠BDE=180°-70°×2=40°,
∴∠AFE=∠EDA+∠A=40°+10°=50°
13. 解:(2)(1)中结论仍成立.
证明:∵△ABC是等边三角形,∴AC=BC,∠ACB=60°.又∵△ECD是等边三角形,∴CE=CD,∠DCE=60°,∴∠ACB=∠DCE=60°,∴∠ACB+∠1=∠DCE+∠1,即∠ACE=∠BCD.
易证△ACE≌△BCD,∴AE=BD,∠2=∠3.
∵∠AFB+∠3=∠ACB+∠2,且∠ACB=60°,∴∠AFB=60°
(3)∵△ABC是等边三角形,∴AC=BC=4,
当旋转60°时,B,C,D三点共线,此时BD最大,最大为BC+CD=7;当旋转240°时,B,C,D三点共线,此时BD最小,最小为BC-CD=1,∴1≤BD≤7
同课章节目录
