安徽省皖江名校2023-2024学年高二上学期开学联考数学试题(含解析)
文档属性
| 名称 | 安徽省皖江名校2023-2024学年高二上学期开学联考数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 808.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览




文档简介
姓名 座位号
(在此卷上答题无效)
安徽省皖江名校2023-2024学年高二上学期开学联考
数 学
本试卷共4页,22题。全卷满分150分,考试时间120分钟。
考生注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则的最小值是
A.B.C.D.
2.已知复数()为纯虚数,则复数在复平面内对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知向量,,且,则
A. B. C.1 D.2
4.已知在平面直角坐标系中,点在角终边上,则
A. B. C. D.
5.手工课上某同学用六个边长相等的正方形卡片拼接成一个几何图形,如图所示,其中AB,CD,EF,MN为对角线,该几何图形恰好能折叠组装成一个正方体卡片纸盒,则在正方体卡片纸盒中
A. B. C. D.
6.2013年7月18日,第31届全国青少年爱国主义读书教育活动启动,某校为了迎接此次活动,对本校高一高二年级学生进行了前期阅读时间抽查,得到日阅读时间(单位:分钟)的统计表如下:
年级 抽查人数 平均时间 方差
高一 40 50 4
高二 60 40 6
则估计两个年级学生日阅读时间的方差为
A.52 B.29.2 C.10 D.6.4
7.已知实数a,b,c满足,,,则
A. B. C. D.
8.已知在中,角A,B,C的对边分别为a,b,c,,点Q在边BC上,且满足(),,则的最小值是
A.32 B.64 C.100 D.120
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分。
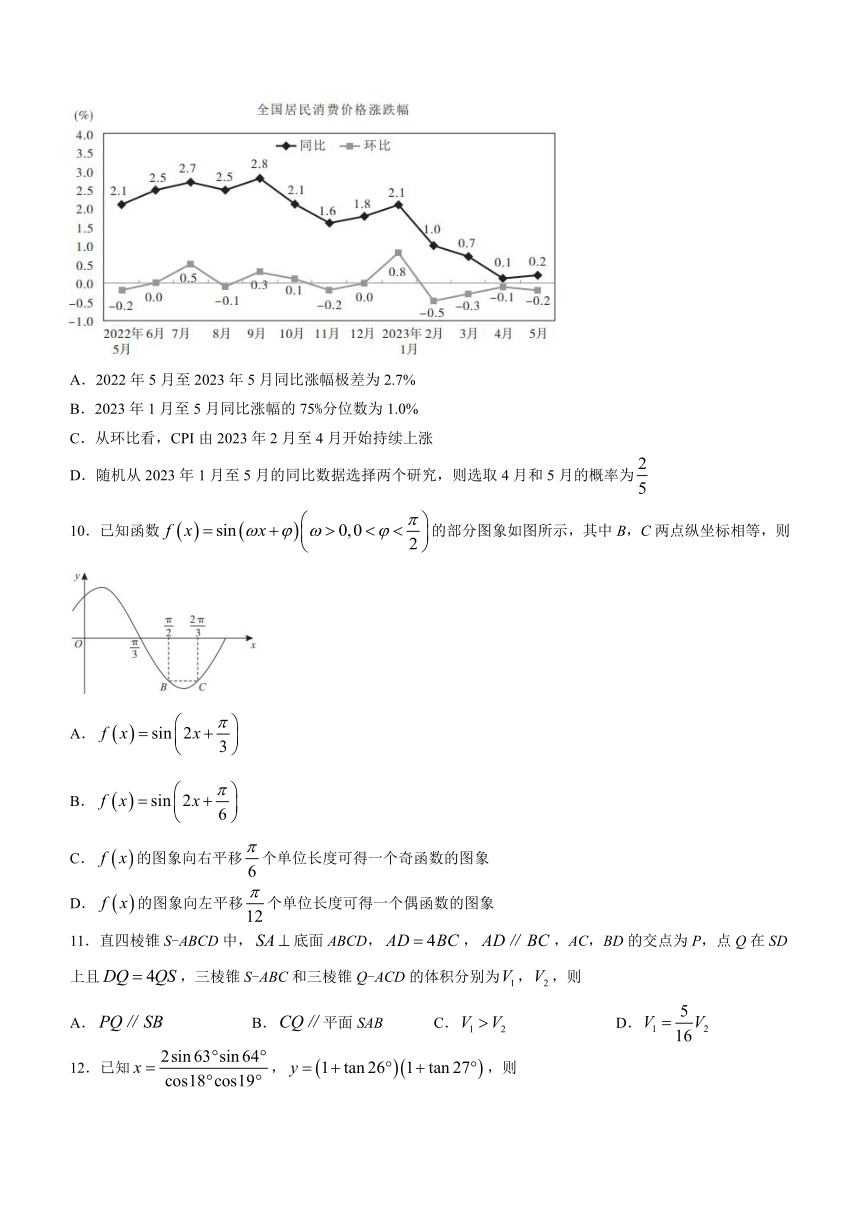
9.CPI是居民消费价格即消费价格指数,是反映居民家庭一般所购买的消费品和服务项目价格水平变动的宏观经济指标.下图是国家统计局发布的2022年5月至2023年5月全国居民消费价格涨跌幅统计图,其中同比是与上年同期对比(如今年5月与上年5月),侧重数据长期趋势,环比是与上月对比(如今年5月与4月),侧重数据短期变化,则下列说过正确的是
A.2022年5月至2023年5月同比涨幅极差为2.7%
B.2023年1月至5月同比涨幅的75%分位数为1.0%
C.从环比看,CPI由2023年2月至4月开始持续上涨
D.随机从2023年1月至5月的同比数据选择两个研究,则选取4月和5月的概率为
10.已知函数的部分图象如图所示,其中B,C两点纵坐标相等,则
A.
B.
C.的图象向右平移个单位长度可得一个奇函数的图象
D.的图象向左平移个单位长度可得一个偶函数的图象
11.直四棱锥S-ABCD中,底面ABCD,,,AC,BD的交点为P,点Q在SD上且,三棱锥S-ABC和三棱锥Q-ACD的体积分别为,,则
A. B.平面SAB C. D.
12.已知,,则
A. B.
C. D.
三、填空题:本题共4小题,每小题5分,共20分。
13.复数,则 .
14.已知正四棱台上下底面边长分别为2和8,侧面梯形的高为5,则该四棱台的体积为 .
15.随着国家“双碳”(碳达峰与碳中和的简称)目标的提出,我国风电发展驶入快车道,陆地、海上的风机(如下左图,顶端外形是大风车,又称风力发电大风车)纷纷“拔地而起”,成为保护环境、输送绿色能源的“风中使者”.如图,一学习兴趣小组为了测量某风力发电大风车AB的高度,在点A正东方点C处测得风车顶端点B的仰角为30°,在点A南偏西30°方向的点D处测得点B的仰角为60°,且C,D相距米,其中平面ADC,则AB的高度为 米.
16.若的定义域为,对于,都有,且满足,,则称为康托尔函数.当时,康托尔函数 ; .
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
设平面向量,满足,,.
(1)求;
(2)求向量在向量上的投影向量(用坐标表示).
18.(12分)
已知在中,角A,B,C的对边分别为a,b,c,且满足.
(1)求角C;
(2)若,,求的面积.
19.(12分)
2023年7月11日第64届国际数学奥林匹克竞赛结果公布,中国队6名参赛选手全员金牌,再夺第一.某班级为了选拔数学竞赛选手,举行初次选拔考试,共有排好顺序的两道解答题.规定全部答对者,通过选拔考试.设甲答对第一道和第二道题的概率分别为,,乙答对第一道和第二道题的概率分别为,,甲,乙相互独立解题,答对与否互不影响.
(1)求甲,乙都通过考试的概率;
(2)记事件“甲、乙共答对两道题”,求.
20.(12分)
如图,D为圆锥的顶点,O是圆锥底面的圆心,P为DO的中点,是底面的内接正三角形.
(1)若底面圆的半径为2,直线PB与底面的夹角为45°,求圆锥侧面展开图的面积;
(2)若,证明:平面平面PAB.
21.(12分)
如图所示,中,AQ为边BC的中线,,,,,其中,,,.
(1)当时,用向量,表示;
(2)证明:为定值.
22.(12分)
已知.
(1)若,且,,求的值;
(2)若函数在区间上没有零点,求的取值范围.
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C C B A B A C AB ACD AD ACD
1.【解析】由,,得.
2.【解析】由复数为纯虚数,可得复数,所以复数,所以在复平面内对应的点为,在第三象限,故选C.
3.【解析】由题意可得,因为,所以,解得,故选C.
4.【解析】由题意可得,所以原式,故选B.
5.A
【解析】由题意可得正方体卡片纸盒如图所示,则易知,,CM与CD,MN的夹角均为60°,故选A.
6.【解析】由题意估计高一高二日阅读时间的平均数为,
方差为,故选B.
7.【解析】由,得,即,即.
,
,综上可知,故选A.
8.【解析】因为,分别是向量,的单位向量,所以由(),易知AQ是中角A平分线,于是结合,可得,
,化简得,故,
所以,当且仅当,时等号成立,故选C.
9.【解析】A选项中的极差为,故A正确;B选项中的数据由小到大排列为0.1%,0.2%,0.7%,1.0%,2.1%,由,不是整数,所以75%分位数为第4个数1.0%,故B正确;C选项中2月至4月均为负数,说明下降,故C错误;D选项等价于从5个数字中随机选取2个,样本空间包含的样本点总数为10,其中随机事件“选到4月和5月”包含的样本点数为1,古典概型概率计算公式可得所求概率为,故D错误.综上,选AB.
10.【解析】由题意知,所以的图像的一条对称轴方程为,,所以.由于函数图像过,由,,且,得,所以,故A正确,B错误;的图象向右平移个单位长度得到,是奇函数,故C正确;的图象向左平移个单位长度得到,是偶函数,故D正确.故选ACD.
11.【解析】连接PQ,,,所以,又因为,所以,故A正确;过Q作交SA于点M,由,可得,所以四边形BCQM是梯形,CQ与BM的延长线必定相交,故CQ与平面SAB必定相交,故B错误;设直四棱锥S-ABCD的高为H,底面梯形ABCD的高为h,则易得三棱锥S-ABC和三棱锥Q-ACD的高分别为H,,所以,所以C错误,D正确.综上,选AD.
12.【解析】因为
,所以A正确;由正切函数在上恒为正且单调递增得,所以B错误;注意到,所以,同理,于是,故C正确;由基本不等式可得,故D正确.综上,选ACD.
13.【答案】
【解析】,所以.
14.【答案】112
【解析】由题意可知正四棱台的高为,所以该四棱台的体积为.
15.【答案】40
【解析】由题意知,,,,设,则,,在,由余弦定理可得,解得,所以(米).
16.【答案】,
【解析】在中,分别令,得,在中,令,,得,.又令,得,所以,结合对于,都有,可得当时,康托尔函数,反复利用,可得,注意到,所以,故第二空填.(注:第一空2分,第二空3分)
17.【解析】
(1)因为,所以,
又,,所以,
因为,
所以.
(2)设,的夹角,由(1)中可得,故.
因为,所以,
所以向量在向量上的投影向量为
18.【解析】
(1)由,得,所以,
结合余弦定理可知,而,所以.
(2)由正弦定理可得,解得,
又由余弦定理可得,即,
解得,或,
而,所以,
所以的面积
19.【解析】设事件“甲答对了i道题”,事件“乙答对了i道题”,,1,2,
由题意,,,
,,,
(1)由题意得,甲,乙都通过考试的概率:.
(2)由题意得,,
所以.
20.【解析】
(1)连接OB,由题意知平面ABC,故,则直线PB与底面的夹角为.
因为底面圆的半径为2,所以,底面圆的周长为,
而P为DO的中点,所以,所以圆锥的母线长为,
所以圆锥侧面展开图的面积为.
(2)证明:连接OA,OC,
∵P在DO上,,
∴,
∵是圆内接正三角形,
∴,所以,,
∴,即,,,
∴平面PAB,平面PAC,
∴平面平面PAB.
21.【解析】
(1)当时,,
因为AQ为边BC的中线,
所以,
所以.
(2)证明:由(1)可知,
所以.
而,,,
所以,
即,
整理可得,
而,是不共线向量,所以,
消去x,可得定值).
22.【解析】
(1)
,
因为,所以.
由得,
而,所以,
所以,,
故
.
(2)由(1)知,
因为函数,,,
在区间上没有零点,
所以,
即,,
因为,所以,
又因为,
所以,
所以,
所以,
因为,所以或,
当时,;
当时,,
又因为,所以的取值范围是.
(在此卷上答题无效)
安徽省皖江名校2023-2024学年高二上学期开学联考
数 学
本试卷共4页,22题。全卷满分150分,考试时间120分钟。
考生注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则的最小值是
A.B.C.D.
2.已知复数()为纯虚数,则复数在复平面内对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知向量,,且,则
A. B. C.1 D.2
4.已知在平面直角坐标系中,点在角终边上,则
A. B. C. D.
5.手工课上某同学用六个边长相等的正方形卡片拼接成一个几何图形,如图所示,其中AB,CD,EF,MN为对角线,该几何图形恰好能折叠组装成一个正方体卡片纸盒,则在正方体卡片纸盒中
A. B. C. D.
6.2013年7月18日,第31届全国青少年爱国主义读书教育活动启动,某校为了迎接此次活动,对本校高一高二年级学生进行了前期阅读时间抽查,得到日阅读时间(单位:分钟)的统计表如下:
年级 抽查人数 平均时间 方差
高一 40 50 4
高二 60 40 6
则估计两个年级学生日阅读时间的方差为
A.52 B.29.2 C.10 D.6.4
7.已知实数a,b,c满足,,,则
A. B. C. D.
8.已知在中,角A,B,C的对边分别为a,b,c,,点Q在边BC上,且满足(),,则的最小值是
A.32 B.64 C.100 D.120
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分。
9.CPI是居民消费价格即消费价格指数,是反映居民家庭一般所购买的消费品和服务项目价格水平变动的宏观经济指标.下图是国家统计局发布的2022年5月至2023年5月全国居民消费价格涨跌幅统计图,其中同比是与上年同期对比(如今年5月与上年5月),侧重数据长期趋势,环比是与上月对比(如今年5月与4月),侧重数据短期变化,则下列说过正确的是
A.2022年5月至2023年5月同比涨幅极差为2.7%
B.2023年1月至5月同比涨幅的75%分位数为1.0%
C.从环比看,CPI由2023年2月至4月开始持续上涨
D.随机从2023年1月至5月的同比数据选择两个研究,则选取4月和5月的概率为
10.已知函数的部分图象如图所示,其中B,C两点纵坐标相等,则
A.
B.
C.的图象向右平移个单位长度可得一个奇函数的图象
D.的图象向左平移个单位长度可得一个偶函数的图象
11.直四棱锥S-ABCD中,底面ABCD,,,AC,BD的交点为P,点Q在SD上且,三棱锥S-ABC和三棱锥Q-ACD的体积分别为,,则
A. B.平面SAB C. D.
12.已知,,则
A. B.
C. D.
三、填空题:本题共4小题,每小题5分,共20分。
13.复数,则 .
14.已知正四棱台上下底面边长分别为2和8,侧面梯形的高为5,则该四棱台的体积为 .
15.随着国家“双碳”(碳达峰与碳中和的简称)目标的提出,我国风电发展驶入快车道,陆地、海上的风机(如下左图,顶端外形是大风车,又称风力发电大风车)纷纷“拔地而起”,成为保护环境、输送绿色能源的“风中使者”.如图,一学习兴趣小组为了测量某风力发电大风车AB的高度,在点A正东方点C处测得风车顶端点B的仰角为30°,在点A南偏西30°方向的点D处测得点B的仰角为60°,且C,D相距米,其中平面ADC,则AB的高度为 米.
16.若的定义域为,对于,都有,且满足,,则称为康托尔函数.当时,康托尔函数 ; .
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
设平面向量,满足,,.
(1)求;
(2)求向量在向量上的投影向量(用坐标表示).
18.(12分)
已知在中,角A,B,C的对边分别为a,b,c,且满足.
(1)求角C;
(2)若,,求的面积.
19.(12分)
2023年7月11日第64届国际数学奥林匹克竞赛结果公布,中国队6名参赛选手全员金牌,再夺第一.某班级为了选拔数学竞赛选手,举行初次选拔考试,共有排好顺序的两道解答题.规定全部答对者,通过选拔考试.设甲答对第一道和第二道题的概率分别为,,乙答对第一道和第二道题的概率分别为,,甲,乙相互独立解题,答对与否互不影响.
(1)求甲,乙都通过考试的概率;
(2)记事件“甲、乙共答对两道题”,求.
20.(12分)
如图,D为圆锥的顶点,O是圆锥底面的圆心,P为DO的中点,是底面的内接正三角形.
(1)若底面圆的半径为2,直线PB与底面的夹角为45°,求圆锥侧面展开图的面积;
(2)若,证明:平面平面PAB.
21.(12分)
如图所示,中,AQ为边BC的中线,,,,,其中,,,.
(1)当时,用向量,表示;
(2)证明:为定值.
22.(12分)
已知.
(1)若,且,,求的值;
(2)若函数在区间上没有零点,求的取值范围.
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C C B A B A C AB ACD AD ACD
1.【解析】由,,得.
2.【解析】由复数为纯虚数,可得复数,所以复数,所以在复平面内对应的点为,在第三象限,故选C.
3.【解析】由题意可得,因为,所以,解得,故选C.
4.【解析】由题意可得,所以原式,故选B.
5.A
【解析】由题意可得正方体卡片纸盒如图所示,则易知,,CM与CD,MN的夹角均为60°,故选A.
6.【解析】由题意估计高一高二日阅读时间的平均数为,
方差为,故选B.
7.【解析】由,得,即,即.
,
,综上可知,故选A.
8.【解析】因为,分别是向量,的单位向量,所以由(),易知AQ是中角A平分线,于是结合,可得,
,化简得,故,
所以,当且仅当,时等号成立,故选C.
9.【解析】A选项中的极差为,故A正确;B选项中的数据由小到大排列为0.1%,0.2%,0.7%,1.0%,2.1%,由,不是整数,所以75%分位数为第4个数1.0%,故B正确;C选项中2月至4月均为负数,说明下降,故C错误;D选项等价于从5个数字中随机选取2个,样本空间包含的样本点总数为10,其中随机事件“选到4月和5月”包含的样本点数为1,古典概型概率计算公式可得所求概率为,故D错误.综上,选AB.
10.【解析】由题意知,所以的图像的一条对称轴方程为,,所以.由于函数图像过,由,,且,得,所以,故A正确,B错误;的图象向右平移个单位长度得到,是奇函数,故C正确;的图象向左平移个单位长度得到,是偶函数,故D正确.故选ACD.
11.【解析】连接PQ,,,所以,又因为,所以,故A正确;过Q作交SA于点M,由,可得,所以四边形BCQM是梯形,CQ与BM的延长线必定相交,故CQ与平面SAB必定相交,故B错误;设直四棱锥S-ABCD的高为H,底面梯形ABCD的高为h,则易得三棱锥S-ABC和三棱锥Q-ACD的高分别为H,,所以,所以C错误,D正确.综上,选AD.
12.【解析】因为
,所以A正确;由正切函数在上恒为正且单调递增得,所以B错误;注意到,所以,同理,于是,故C正确;由基本不等式可得,故D正确.综上,选ACD.
13.【答案】
【解析】,所以.
14.【答案】112
【解析】由题意可知正四棱台的高为,所以该四棱台的体积为.
15.【答案】40
【解析】由题意知,,,,设,则,,在,由余弦定理可得,解得,所以(米).
16.【答案】,
【解析】在中,分别令,得,在中,令,,得,.又令,得,所以,结合对于,都有,可得当时,康托尔函数,反复利用,可得,注意到,所以,故第二空填.(注:第一空2分,第二空3分)
17.【解析】
(1)因为,所以,
又,,所以,
因为,
所以.
(2)设,的夹角,由(1)中可得,故.
因为,所以,
所以向量在向量上的投影向量为
18.【解析】
(1)由,得,所以,
结合余弦定理可知,而,所以.
(2)由正弦定理可得,解得,
又由余弦定理可得,即,
解得,或,
而,所以,
所以的面积
19.【解析】设事件“甲答对了i道题”,事件“乙答对了i道题”,,1,2,
由题意,,,
,,,
(1)由题意得,甲,乙都通过考试的概率:.
(2)由题意得,,
所以.
20.【解析】
(1)连接OB,由题意知平面ABC,故,则直线PB与底面的夹角为.
因为底面圆的半径为2,所以,底面圆的周长为,
而P为DO的中点,所以,所以圆锥的母线长为,
所以圆锥侧面展开图的面积为.
(2)证明:连接OA,OC,
∵P在DO上,,
∴,
∵是圆内接正三角形,
∴,所以,,
∴,即,,,
∴平面PAB,平面PAC,
∴平面平面PAB.
21.【解析】
(1)当时,,
因为AQ为边BC的中线,
所以,
所以.
(2)证明:由(1)可知,
所以.
而,,,
所以,
即,
整理可得,
而,是不共线向量,所以,
消去x,可得定值).
22.【解析】
(1)
,
因为,所以.
由得,
而,所以,
所以,,
故
.
(2)由(1)知,
因为函数,,,
在区间上没有零点,
所以,
即,,
因为,所以,
又因为,
所以,
所以,
所以,
因为,所以或,
当时,;
当时,,
又因为,所以的取值范围是.
同课章节目录
