2023-2024学年人教版数学八年级上册12.1全等三角形 同步练习(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册12.1全等三角形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 136.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 00:00:00 | ||
图片预览

文档简介
12.1全等三角形 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.全等形是指( )
A.形状相同的两个图形 B.面积相同的两个图形
C.两张中国地形图,两个等腰三角形都是全等形 D.能够完全重合的两个平面图形
2.如图,△ABC≌△DEF,则∠E的度数为( )
A.80° B.40° C.62° D.38°
3.如图,,,.则的度数为( )
A. B. C. D.
4.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,在下列结论中,不正确的是( )
A.∠EAB=∠FAC B.BC=EF
C.∠BAC=∠CAF D.∠AFE=∠ACB
5.△ABC与△DFE是全等三角形,A与D对应,B与F对应,则按标有字母的线段计算,图中相等的线段有( )
A.1组 B.2组 C.3组 D.4组
6.如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,BF=7cm,则BE长为( )
A.1cm B.2cm C.3cm D.4cm
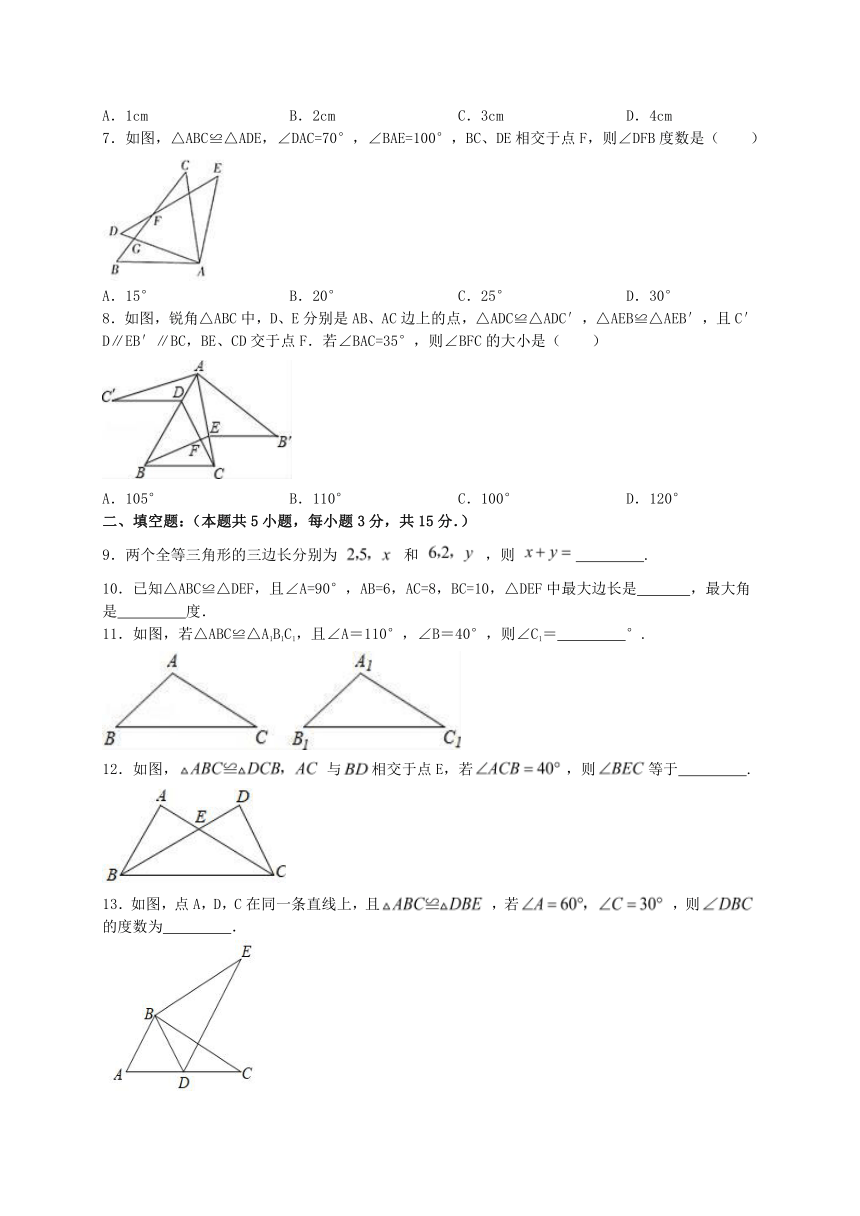
7.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A.15° B.20° C.25° D.30°
8.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.两个全等三角形的三边长分别为 和 ,则 .
10.已知△ABC≌△DEF,且∠A=90°,AB=6,AC=8,BC=10,△DEF中最大边长是 ,最大角是 度.
11.如图,若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1= °.
12.如图,与相交于点E,若,则等于 .
13.如图,点A,D,C在同一条直线上,且,若,则的度数为 .
三、解答题:(本题共5题,共45分)
14.如图,请沿图中的虚线,用三种方法将下列图形(3×4网格)划分为两个全等图形.
15.如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
16.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.
17.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm,求:
(1)∠1的度数;
(2)AC的长.
18.如图,△ABD≌△EBC,AB=3cm,BC=6cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
参考答案:
1.D 2.D 3.C 4.C 5.D 6.B 7.A 8.B
9.11
10.10;90
11.30
12.100°
13.30°
14. 解:如图
15.解:∵△ABO≌△CDO,
∴OB=OD,∠ABO=∠D,
∴∠OBD=∠D= (180°-∠BOD)= (180°-30)=75°,
∴∠ABC=180°-75°×2=30°,
∵AO∥CD
∴∠A=∠ABC=30°.
16.解:∵ △ABC≌△ADE,
∴∠DAE=∠BAC,
∴∠DAE+∠BAC+∠CAD=105°,
∴2∠BAC=105°-∠CAD=70°,
∴∠BAC=35°,
∴∠BAF=∠BAC+∠CAD=35°+35°=70°,
∴∠BFD=∠B+∠BAF=20°+70°=90°,
∴∠BED=∠BFD-∠D=90°-20°=70°.
17.(1)解:∵△ADF≌△BCE,
∴∠F=∠E=22°,
∵∠1是△BCE的一个外角,
∴∠1=∠B+∠E=40°+22°=62°
(2)∵△ADF≌△BCE,
∴AD=BC=2cm,
∴AC=AD+DC=2+1=3cm
18.(1)解:∵△ABD≌△EBC ∴AB=BE,BD=BC∵AB=3 BC=6 DE=BD-BE=BC-AB=6-3=3.
(2)垂直. ∵△ABD≌△EBC,且A、B、C在一条直线上,∴∠ABD=∠CBE=90 故DB⊥AC
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.全等形是指( )
A.形状相同的两个图形 B.面积相同的两个图形
C.两张中国地形图,两个等腰三角形都是全等形 D.能够完全重合的两个平面图形
2.如图,△ABC≌△DEF,则∠E的度数为( )
A.80° B.40° C.62° D.38°
3.如图,,,.则的度数为( )
A. B. C. D.
4.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,在下列结论中,不正确的是( )
A.∠EAB=∠FAC B.BC=EF
C.∠BAC=∠CAF D.∠AFE=∠ACB
5.△ABC与△DFE是全等三角形,A与D对应,B与F对应,则按标有字母的线段计算,图中相等的线段有( )
A.1组 B.2组 C.3组 D.4组
6.如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5cm,BF=7cm,则BE长为( )
A.1cm B.2cm C.3cm D.4cm
7.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A.15° B.20° C.25° D.30°
8.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
二、填空题:(本题共5小题,每小题3分,共15分.)
9.两个全等三角形的三边长分别为 和 ,则 .
10.已知△ABC≌△DEF,且∠A=90°,AB=6,AC=8,BC=10,△DEF中最大边长是 ,最大角是 度.
11.如图,若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1= °.
12.如图,与相交于点E,若,则等于 .
13.如图,点A,D,C在同一条直线上,且,若,则的度数为 .
三、解答题:(本题共5题,共45分)
14.如图,请沿图中的虚线,用三种方法将下列图形(3×4网格)划分为两个全等图形.
15.如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.
16.如图,△ABC≌△ADE,且∠CAD=35°,∠B=∠D=20°,∠EAB=105°,求∠BFD和∠BED的度数.
17.如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm,求:
(1)∠1的度数;
(2)AC的长.
18.如图,△ABD≌△EBC,AB=3cm,BC=6cm,
(1)求DE的长.
(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?
参考答案:
1.D 2.D 3.C 4.C 5.D 6.B 7.A 8.B
9.11
10.10;90
11.30
12.100°
13.30°
14. 解:如图
15.解:∵△ABO≌△CDO,
∴OB=OD,∠ABO=∠D,
∴∠OBD=∠D= (180°-∠BOD)= (180°-30)=75°,
∴∠ABC=180°-75°×2=30°,
∵AO∥CD
∴∠A=∠ABC=30°.
16.解:∵ △ABC≌△ADE,
∴∠DAE=∠BAC,
∴∠DAE+∠BAC+∠CAD=105°,
∴2∠BAC=105°-∠CAD=70°,
∴∠BAC=35°,
∴∠BAF=∠BAC+∠CAD=35°+35°=70°,
∴∠BFD=∠B+∠BAF=20°+70°=90°,
∴∠BED=∠BFD-∠D=90°-20°=70°.
17.(1)解:∵△ADF≌△BCE,
∴∠F=∠E=22°,
∵∠1是△BCE的一个外角,
∴∠1=∠B+∠E=40°+22°=62°
(2)∵△ADF≌△BCE,
∴AD=BC=2cm,
∴AC=AD+DC=2+1=3cm
18.(1)解:∵△ABD≌△EBC ∴AB=BE,BD=BC∵AB=3 BC=6 DE=BD-BE=BC-AB=6-3=3.
(2)垂直. ∵△ABD≌△EBC,且A、B、C在一条直线上,∴∠ABD=∠CBE=90 故DB⊥AC
