2023-2024学年人教版数学八年级上册13.1轴对称 同步练习(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册13.1轴对称 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 259.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 15:23:46 | ||
图片预览

文档简介
13.1轴对称 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.2022年卡塔尔世界杯是自1930年以来举办的第22届世界杯,历届世界杯可谓各具特色,会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中,属于轴对称图形的是( )
A. B. C. D.
2.如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )
A.50° B.100° C.120° D.130°
3.如图,在△ABC中,DE是AC的垂直平分线,分别交BC,AC于D,E两点,若∠B=80°,∠C=35°,则∠BAD的度数为( )
A.65° B.35° C.30° D.25°
4.如图,和关于直线对称,下列结论:①;②;③直线垂直平分;④直线平分.正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
A.18cm B.22cm C.24cm D.26cm
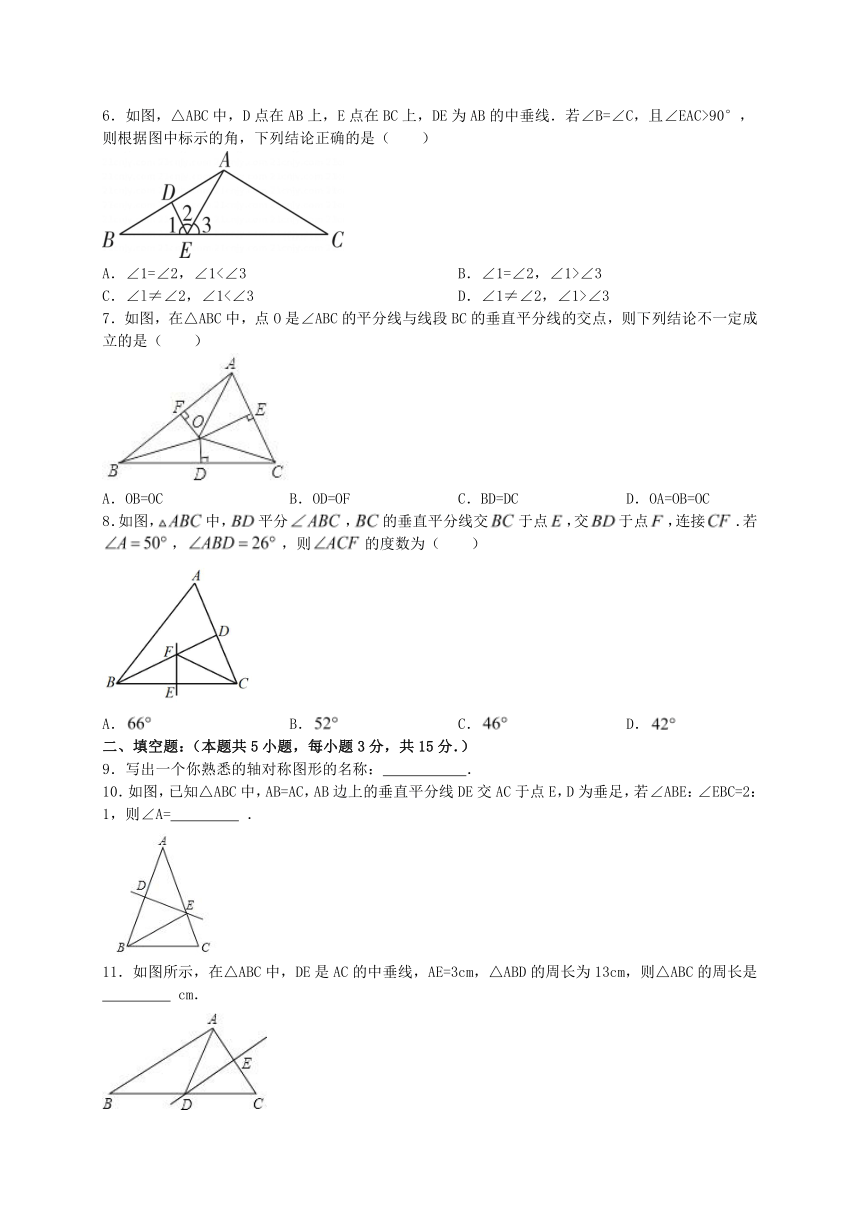
6.如图,△ABC中,D点在AB上,E点在BC上,DE为AB的中垂线.若∠B=∠C,且∠EAC>90°,则根据图中标示的角,下列结论正确的是( )
A.∠1=∠2,∠1<∠3 B.∠1=∠2,∠1>∠3
C.∠l≠∠2,∠1<∠3 D.∠1≠∠2,∠1>∠3
7.如图,在△ABC中,点O是∠ABC的平分线与线段BC的垂直平分线的交点,则下列结论不一定成立的是( )
A.OB=OC B.OD=OF C.BD=DC D.OA=OB=OC
8.如图,中,平分,的垂直平分线交于点,交于点,连接.若,,则的度数为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.写出一个你熟悉的轴对称图形的名称: .
10.如图,已知△ABC中,AB=AC,AB边上的垂直平分线DE交AC于点E,D为垂足,若∠ABE:∠EBC=2:1,则∠A= .
11.如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是
cm.
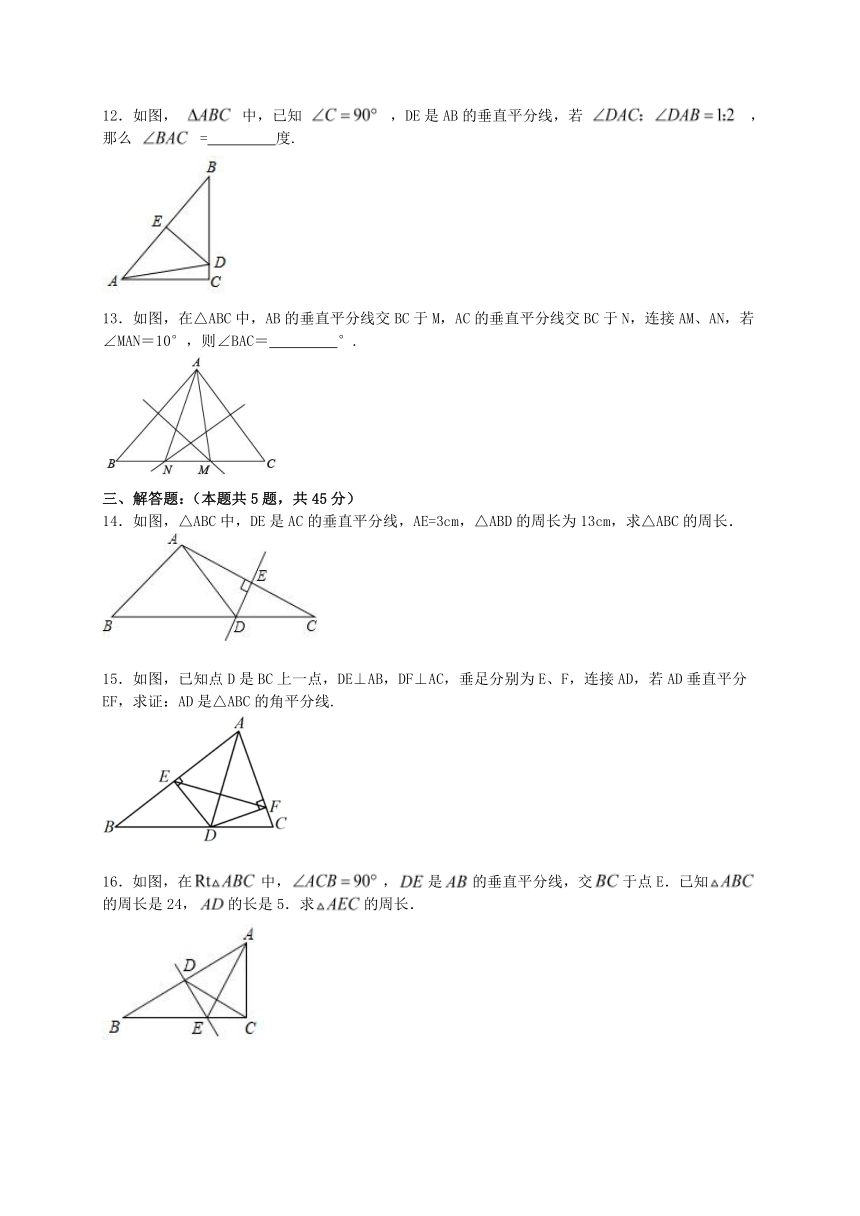
12.如图, 中,已知 ,DE是AB的垂直平分线,若 ,那么 = 度.
13.如图,在△ABC中,AB的垂直平分线交BC于M,AC的垂直平分线交BC于N,连接AM、AN,若∠MAN=10°,则∠BAC= °.
三、解答题:(本题共5题,共45分)
14.如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
15.如图,已知点D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F,连接AD,若AD垂直平分EF,求证:AD是△ABC的角平分线.
16.如图,在中,,是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
17.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58°
(1)求出BF的长度;
(2)求∠CAD的度数;
18.如图,在△ABC 中,AB=7,BC=14,M为AC的中点,OM⊥AC 交 的平分线于O,OE⊥AB交BA的延长线于E,OF⊥BC.垂足为F.
(1)求证:AE=CF.
(2)求线段BE的长.
参考答案:
1.D 2.B 3.C 4.D 5.B 6.B 7.D 8.B
9.答案不唯一(如:线段、角等)
10.45°
11.19
12.54
13.85
14.解:∵DE是AC的垂直平分线,AE=3cm,
∴AD=CD,AC=2AE=2×3=6cm,
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
15.证明:∵AD垂直平分EF,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
16.解:∵是的垂直平分线,
∴,,
∵,
∴,
∵的周长为24,
∴,
∵
∴的周长为14.
17.(1)解:∵△ABC与△ADE关于直线MN对称,ED=4cm,
∴BC=ED=4cm,
又∵FC=1cm,
∴BF=BC﹣FC=3cm.
(2)解:∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD﹣∠EAC=76°﹣58°=18°
18.(1)解:连接OA
∵OB平分 ,
又∵OE⊥AB,OF⊥BC,
∴OE=OF.
∵OM⊥AC,M为AC中点,
∴OM垂直平分AC,
∴OA=OC,
∴△AEO≌△CFO(HL),
∴AE=CF.
(2)解:∵OB平分
∴
又∵OE⊥AB,OF⊥BC
∴
又OB=OB
∴△BEO≌△BFO(AAS),
∴BE=BF.
∵AB=7,BC=14,
设AE=CF=x,
∴x+7=14-x,
,
∴BE=7+
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.2022年卡塔尔世界杯是自1930年以来举办的第22届世界杯,历届世界杯可谓各具特色,会徽设计也蕴含了不同的文化.下列世界杯会徽的图案中,属于轴对称图形的是( )
A. B. C. D.
2.如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )
A.50° B.100° C.120° D.130°
3.如图,在△ABC中,DE是AC的垂直平分线,分别交BC,AC于D,E两点,若∠B=80°,∠C=35°,则∠BAD的度数为( )
A.65° B.35° C.30° D.25°
4.如图,和关于直线对称,下列结论:①;②;③直线垂直平分;④直线平分.正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
A.18cm B.22cm C.24cm D.26cm
6.如图,△ABC中,D点在AB上,E点在BC上,DE为AB的中垂线.若∠B=∠C,且∠EAC>90°,则根据图中标示的角,下列结论正确的是( )
A.∠1=∠2,∠1<∠3 B.∠1=∠2,∠1>∠3
C.∠l≠∠2,∠1<∠3 D.∠1≠∠2,∠1>∠3
7.如图,在△ABC中,点O是∠ABC的平分线与线段BC的垂直平分线的交点,则下列结论不一定成立的是( )
A.OB=OC B.OD=OF C.BD=DC D.OA=OB=OC
8.如图,中,平分,的垂直平分线交于点,交于点,连接.若,,则的度数为( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.写出一个你熟悉的轴对称图形的名称: .
10.如图,已知△ABC中,AB=AC,AB边上的垂直平分线DE交AC于点E,D为垂足,若∠ABE:∠EBC=2:1,则∠A= .
11.如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是
cm.
12.如图, 中,已知 ,DE是AB的垂直平分线,若 ,那么 = 度.
13.如图,在△ABC中,AB的垂直平分线交BC于M,AC的垂直平分线交BC于N,连接AM、AN,若∠MAN=10°,则∠BAC= °.
三、解答题:(本题共5题,共45分)
14.如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长.
15.如图,已知点D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F,连接AD,若AD垂直平分EF,求证:AD是△ABC的角平分线.
16.如图,在中,,是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
17.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58°
(1)求出BF的长度;
(2)求∠CAD的度数;
18.如图,在△ABC 中,AB=7,BC=14,M为AC的中点,OM⊥AC 交 的平分线于O,OE⊥AB交BA的延长线于E,OF⊥BC.垂足为F.
(1)求证:AE=CF.
(2)求线段BE的长.
参考答案:
1.D 2.B 3.C 4.D 5.B 6.B 7.D 8.B
9.答案不唯一(如:线段、角等)
10.45°
11.19
12.54
13.85
14.解:∵DE是AC的垂直平分线,AE=3cm,
∴AD=CD,AC=2AE=2×3=6cm,
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
15.证明:∵AD垂直平分EF,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
16.解:∵是的垂直平分线,
∴,,
∵,
∴,
∵的周长为24,
∴,
∵
∴的周长为14.
17.(1)解:∵△ABC与△ADE关于直线MN对称,ED=4cm,
∴BC=ED=4cm,
又∵FC=1cm,
∴BF=BC﹣FC=3cm.
(2)解:∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD﹣∠EAC=76°﹣58°=18°
18.(1)解:连接OA
∵OB平分 ,
又∵OE⊥AB,OF⊥BC,
∴OE=OF.
∵OM⊥AC,M为AC中点,
∴OM垂直平分AC,
∴OA=OC,
∴△AEO≌△CFO(HL),
∴AE=CF.
(2)解:∵OB平分
∴
又∵OE⊥AB,OF⊥BC
∴
又OB=OB
∴△BEO≌△BFO(AAS),
∴BE=BF.
∵AB=7,BC=14,
设AE=CF=x,
∴x+7=14-x,
,
∴BE=7+
