11.2与三角形有关的角 同步练习 2023-2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 11.2与三角形有关的角 同步练习 2023-2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 15:33:06 | ||
图片预览

文档简介
11.2与三角形有关的角 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.在中,,则是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
2.在中,,则的度数为( )
A. B. C. D.
3.如图,∠1=100°,∠2=145°,那么∠3=( )
A.55° B.65° C.75° D.85°
4.如图,直线a∥b,点C,D分别在直线b,a上,AC⊥BC,CD平分∠ACB,若∠1=70°,则∠2的度数为( )
A.65° B.70° C.75° D.80°
5.如图,将一副直角三角板,按如图所示叠放在一起,则图中的度数是( )
A. B. C. D.
6.如图,△ABC中,∠ABC,∠ACB的三等分线交于点E,D,若 ,则∠BDC的度数为( )
A. B. C. D.
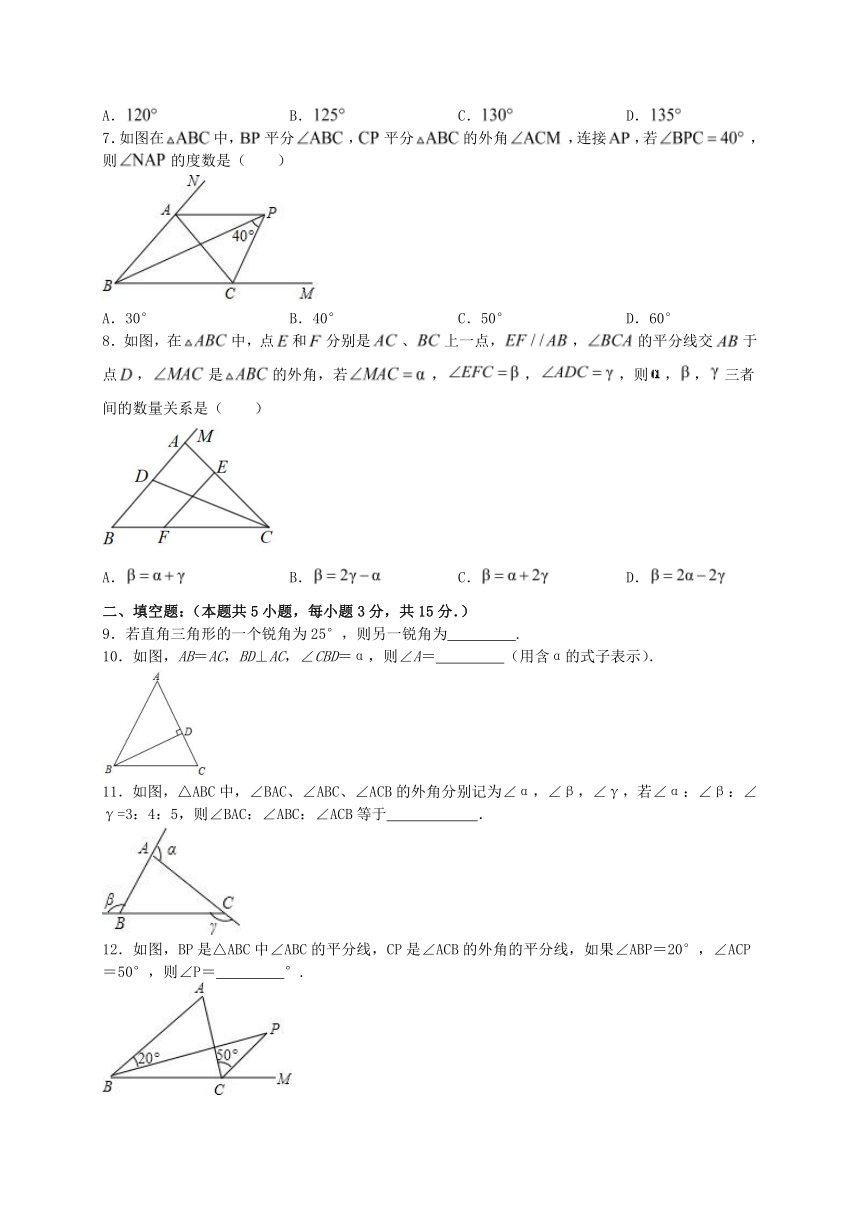
7.如图在中,平分,平分的外角,连接,若,则的度数是( )
A.30° B.40° C.50° D.60°
8.如图,在中,点和分别是、上一点,,的平分线交于点,是的外角,若,,,则,,三者间的数量关系是( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.若直角三角形的一个锐角为25°,则另一锐角为 .
10.如图,AB=AC,BD⊥AC,∠CBD=α,则∠A= (用含α的式子表示).
11.如图,△ABC中,∠BAC、∠ABC、∠ACB的外角分别记为∠α,∠β,∠γ,若∠α:∠β:∠γ=3:4:5,则∠BAC:∠ABC:∠ACB等于 .
12.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P= °.
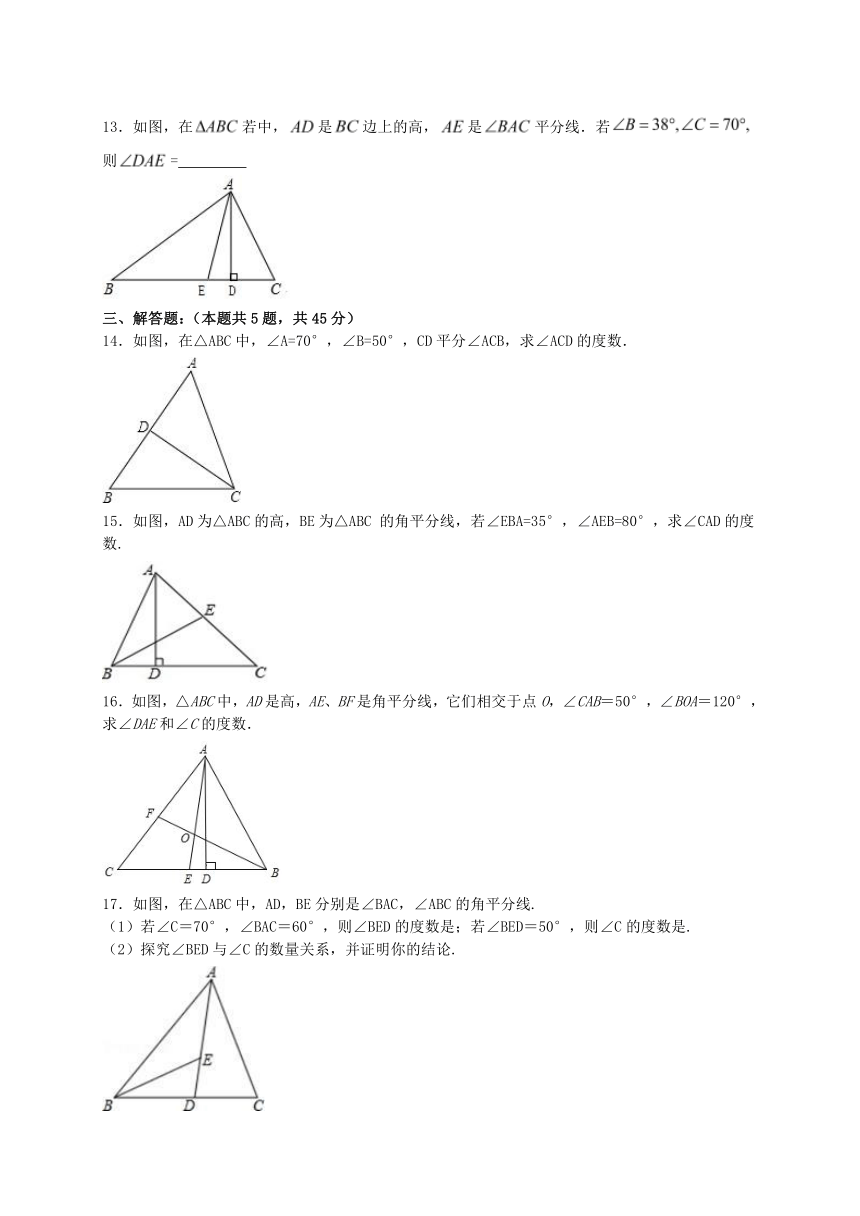
13.如图,在若中,是边上的高,是平分线.若则=
三、解答题:(本题共5题,共45分)
14.如图,在△ABC中,∠A=70°,∠B=50°,CD平分∠ACB,求∠ACD的度数.
15.如图,AD为△ABC的高,BE为△ABC 的角平分线,若∠EBA=35°,∠AEB=80°,求∠CAD的度数.
16.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠BOA=120°,求∠DAE和∠C的度数.
17.如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的角平分线.
(1)若∠C=70°,∠BAC=60°,则∠BED的度数是;若∠BED=50°,则∠C的度数是.
(2)探究∠BED与∠C的数量关系,并证明你的结论.
18.如图所示,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BP平分∠ABC交AD于点P.(1)求∠APB的度数.
(2)若∠ADC=56°,求∠ABP的度数.
参考答案:
1.A 2.C 3.B 4.A 5.B 6.D 7.C 8.B
9.65°
10.2α
11.3:2:1
12.30
13.16°
14.解:∵∠A=70°,∠B=50°,
∴∠ACB=180°﹣70°﹣50°=60°(三角形内角和定义).
∵CD平分∠ACB,
∴∠ACD= ∠ACB= ×60°=30°
15.解:在 中,
为角平分线,
在 中,
在 中,
16.解:∵AE是角平分线,∠CAB=50°,
∴ ,
∵∠BOA=120°,
∴ ,
∵BF是角平分线,
∴ ,
∴ ;
∴ ,
∵AD是高,
∴ .
17.(1)解:∵∠C=70°,∠BAC=60°,
∴∠ABC=50°,
∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠CAD= ∠BAC=30°,∠DBE= ∠ABC=25°,
∵∠ADB=∠DAC+∠C=100°,
∴∠BED=180°﹣100°﹣25°=55°,
∵∠BED=50°,
∴∠ABE+∠BAE=50°,
∴∠ABC+∠BAC=2×50°=100°,
∴∠C=80°;
故答案为:55°,80°
(2)证明:∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠ABE=∠ABC,∠BAE= ∠BAC,
∵∠BED=∠ABE+∠BAE= (∠ABC+∠BAC)= (180°﹣∠C)=90°﹣ ∠C.
18.(1)解:∵∠ACB=90°且∠ACB+∠ABC+∠CAB=180°,
∴∠ABC+∠CAB=90°,
∵AD、BP分别平分∠CAB、∠ABC,
∴
∵∠PBA+∠PAB+∠ABP=180°
∴∠APB=135°
(2)解:∵∠BPD+∠ABP=180°, ∠APB =135°
∴∠BPD=45°
∵∠ADC=56°,且∠PBD+∠BPD=∠ADC
∴∠PBD=56°-45°=11°
即∠ABP=11°
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.在中,,则是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
2.在中,,则的度数为( )
A. B. C. D.
3.如图,∠1=100°,∠2=145°,那么∠3=( )
A.55° B.65° C.75° D.85°
4.如图,直线a∥b,点C,D分别在直线b,a上,AC⊥BC,CD平分∠ACB,若∠1=70°,则∠2的度数为( )
A.65° B.70° C.75° D.80°
5.如图,将一副直角三角板,按如图所示叠放在一起,则图中的度数是( )
A. B. C. D.
6.如图,△ABC中,∠ABC,∠ACB的三等分线交于点E,D,若 ,则∠BDC的度数为( )
A. B. C. D.
7.如图在中,平分,平分的外角,连接,若,则的度数是( )
A.30° B.40° C.50° D.60°
8.如图,在中,点和分别是、上一点,,的平分线交于点,是的外角,若,,,则,,三者间的数量关系是( )
A. B. C. D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.若直角三角形的一个锐角为25°,则另一锐角为 .
10.如图,AB=AC,BD⊥AC,∠CBD=α,则∠A= (用含α的式子表示).
11.如图,△ABC中,∠BAC、∠ABC、∠ACB的外角分别记为∠α,∠β,∠γ,若∠α:∠β:∠γ=3:4:5,则∠BAC:∠ABC:∠ACB等于 .
12.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P= °.
13.如图,在若中,是边上的高,是平分线.若则=
三、解答题:(本题共5题,共45分)
14.如图,在△ABC中,∠A=70°,∠B=50°,CD平分∠ACB,求∠ACD的度数.
15.如图,AD为△ABC的高,BE为△ABC 的角平分线,若∠EBA=35°,∠AEB=80°,求∠CAD的度数.
16.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠BOA=120°,求∠DAE和∠C的度数.
17.如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的角平分线.
(1)若∠C=70°,∠BAC=60°,则∠BED的度数是;若∠BED=50°,则∠C的度数是.
(2)探究∠BED与∠C的数量关系,并证明你的结论.
18.如图所示,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BP平分∠ABC交AD于点P.(1)求∠APB的度数.
(2)若∠ADC=56°,求∠ABP的度数.
参考答案:
1.A 2.C 3.B 4.A 5.B 6.D 7.C 8.B
9.65°
10.2α
11.3:2:1
12.30
13.16°
14.解:∵∠A=70°,∠B=50°,
∴∠ACB=180°﹣70°﹣50°=60°(三角形内角和定义).
∵CD平分∠ACB,
∴∠ACD= ∠ACB= ×60°=30°
15.解:在 中,
为角平分线,
在 中,
在 中,
16.解:∵AE是角平分线,∠CAB=50°,
∴ ,
∵∠BOA=120°,
∴ ,
∵BF是角平分线,
∴ ,
∴ ;
∴ ,
∵AD是高,
∴ .
17.(1)解:∵∠C=70°,∠BAC=60°,
∴∠ABC=50°,
∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠CAD= ∠BAC=30°,∠DBE= ∠ABC=25°,
∵∠ADB=∠DAC+∠C=100°,
∴∠BED=180°﹣100°﹣25°=55°,
∵∠BED=50°,
∴∠ABE+∠BAE=50°,
∴∠ABC+∠BAC=2×50°=100°,
∴∠C=80°;
故答案为:55°,80°
(2)证明:∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠ABE=∠ABC,∠BAE= ∠BAC,
∵∠BED=∠ABE+∠BAE= (∠ABC+∠BAC)= (180°﹣∠C)=90°﹣ ∠C.
18.(1)解:∵∠ACB=90°且∠ACB+∠ABC+∠CAB=180°,
∴∠ABC+∠CAB=90°,
∵AD、BP分别平分∠CAB、∠ABC,
∴
∵∠PBA+∠PAB+∠ABP=180°
∴∠APB=135°
(2)解:∵∠BPD+∠ABP=180°, ∠APB =135°
∴∠BPD=45°
∵∠ADC=56°,且∠PBD+∠BPD=∠ADC
∴∠PBD=56°-45°=11°
即∠ABP=11°
