我变胖了

课件9张PPT。我变胖了【学习目标】
通过分析图形问题中的数量关系，建立方程解决问题，进一步体会运用方程解决问题的关键是抓住等量关系，认识方程模型的重要性．【回顾】
(1)圆柱体积＝πr2h(r为底面半　　　　　　
　径，h为高)．
(2)长方体体积＝长×宽×高．
(3)正方形面积＝边长×边长　正　　
　方形周长＝边长×4
(4)长方形周长＝2×(长＋宽)　　　　
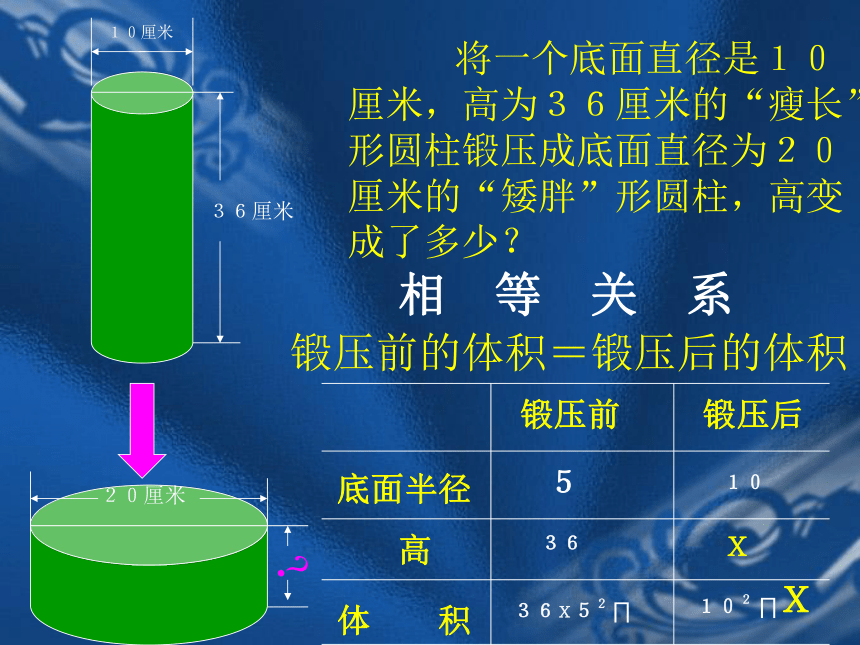
　长方形面积＝长×宽　　　　　将一个底面直径是１０厘米，高为３６厘米的“瘦长”形圆柱锻压成底面直径为２０厘米的“矮胖”形圆柱，高变成了多少？１０厘米３６厘米２０厘米？相　等　关　系锻压前的体积＝锻压后的体积　锻压前锻压后底面半径高体　　积　５３６３６Ｘ５２ ∏１０Ｘ１０２ ∏Ｘ［例1］将内直径为20 cm的圆柱形水桶中的全部水倒入一个长、宽、高分别为30 cm、20 cm、80 cm的长方形铁盒中，正好倒满，求圆柱形水桶的高．(π取3．14)解：设圆柱形水桶高x cm．
π(　　)2·x＝30×20×80　
　
x＝　　　x≈152．79
答：圆柱形水桶高约152．79 cm．点拨：根据题意，由水的体积不变，可知两个容器的容积相同．
V圆柱＝V长方体１０１０１０６１０６(1)形状发生变化，而体积不变．
等量关系：V变化前＝V变化后．
如：将底面半径为r，高为h的圆柱形钢打造成正方体．设正方体棱长为x，则πr2h＝x3．(2)形状发生变化，而面积未变．
等量关系：S变化前＝S变化后．
如：有若干块地砖，摆成正方形时边长为a，若还用这些地砖摆成宽为b的长方形，则长是多少？
设长方形的长为c，则a2＝bc．(3)形状发生变化，而周长未变．
等量关系：变化前的周长＝变化后的周长．
如：用某线绳围成长方形时，长为7，宽为3．若仍用此绳围成一个正方形，边长是多少？
设正方形边长为x，则2×(7＋3)＝4x．(4)若形状、面积、体积、周长均不相等，可是能根据题意找出其中某个量变化前后的关系，可把这个关系作为相等关系．
如：长方体甲的长、宽、高分别为10 cm、20 cm、30 cm，长方体乙的底面是边长为20 cm的正方形，且甲的体积是乙的体积的2倍，求长方体乙的高．
等量关系：V甲＝V乙×2
设乙的高为x cm，则10×20×30＝202·×2x．