【高效备课】北师大版九(上) 第2章 一元二次方程 5 一元二次方程的根与系数的关系 课件
文档属性
| 名称 | 【高效备课】北师大版九(上) 第2章 一元二次方程 5 一元二次方程的根与系数的关系 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1004.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:35:06 | ||
图片预览






文档简介
(共19张PPT)
5 一元二次方程的根与系数的关系
2
北师版九年级上册
复习导入
1. 一元二次方程的一般形式?
ax2 + bx + c = 0 ( a≠0 )
2.一元二次方程有实数根的条件是什么?
△ = b2-4ac ≥ 0
3. 当△>0,△=0,△<0 根的情况如何?
复习导入
△ > 0 时,方程有两个不相等的实数根;
△ = 0 时,方程有两个相等的实数根;
△ < 0 时,方程没有实数根;
4. 一元二次方程的求根公式是什么?
复习导入
同学们,我们来做一个游戏,看谁能更快速的说出下列一元二次方程的两根和与两根积?
(1)x2-2x+1=0 (2)x2 - x-1=0 (3) 2x2-3x +1=0
探究新知
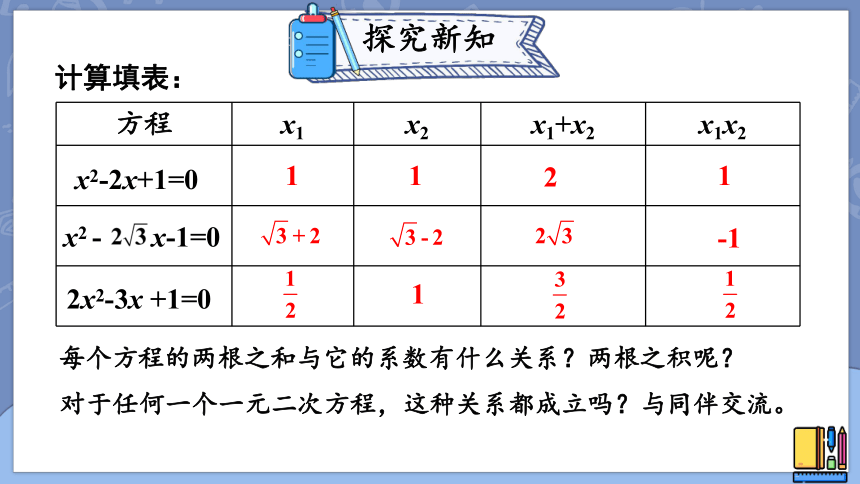
计算填表:
方程 x1 x2 x1+x2 x1x2
x2-2x+1=0
x2 - x-1=0
2x2-3x +1=0
1
1
2
1
-1
1
每个方程的两根之和与它的系数有什么关系?两根之积呢?
对于任何一个一元二次方程,这种关系都成立吗?与同伴交流。
一元二次方程 ax2+bx+c=0(a≠0)当b2-4ac ≥ 0 时有两个根:
x1+x2 =
x1x2 =
如果方程 ax2+bx+c=0(a≠0)有两根实数根x1,x2,那么
x1+x2 =
x1x2 =
例 利用根与系数的关系,求下列方程的两根之和、两根之积:
(1)x2 +7x +6 = 0 ; (2)2x2 - 3x -2 = 0 .
解: (1)这里 a = 1,b = 7,c = 6.
△ =b2-4ac = 72+4×1×6 = 49-24 = 25 > 0
∴方程有两个实数根.
设方程的两个实数根是x1,x2,那么.
x1+x2=-7, x1x2 = 6.
例 利用根与系数的关系,求下列方程的两根之和、两根之积:
(1)x2 +7x +6 = 0 ; (2)2x2 - 3x -2 = 0 .
(2)这里 a = 2,b = -3,c = -2.
△ =b2-4ac = (-3)2-4×2×(-2) = 9+16 = 25 > 0
∴方程有两个实数根.
设方程的两个实数根是x1,x2,那么.
x1+x2= , x1x2 = -1.
随堂练习
【选自教材P50 随堂练习】
利用根与系数的关系,求下列方程的两根之和、两根之积: (1)x2-3x-1=0; (2)3x2+2x-5=0.
解:(1)x1+x2=3, x1x2 = -1.
(2)x1+x2= , x1x2 = .
【选自教材P50 随堂练习】
2. 小明和小华分别求出了方程 9x2+6x-1=0 的根.
小明:x1 = x2 = ;小华:x1 = ,x2 = .
他们的答案正确吗?说说你的判断方法.
x1+x2= ,
x1x2 = .
解:由题意,可得
小明和小华求得的根与算式都不符合,
∴小明和小华的答案都不正确.
【选自教材P50 随堂练习】
3. 已知方程 x2- x-7=0 的一个根是 3 ,求它的另一个根.
解:x1x2 = -7.
x1 = 3.
x2 = .
达标检测
利用根与系数的关系,求下列方程的两根之和、两根之积:
(1)x(3x - 1)-1= 0; (2)(2x + 5) (x+1)= x + 7.
【选自教材P51 习题2.8】
解:(1)3x2-x-1=0.
x1+x2= ,x1x2 = .
(2)x2+3x-1=0.
x1+x2= -3,x1x2 = -1 .
2. 解下列方程:
(1)12x2+7x+1 = 0; (2)0.8x2 + x = 0.3.
(3)3x2+1= x; (4)(x+1)(x-3) = 2x+5.
【选自教材P51 习题2.8】
解:(1)
△ > 0
x1+x2= ,x1x2 = .
x1=
x2=
(2)
△ > 0
x1+x2= ,x1x2 = .
x1=
x2=
2. 解下列方程:
(1)12x2+7x+1 = 0; (2)0.8x2 + x = 0.3.
(3)3x2+1= x; (4)(x+1)(x-3) = 2x+5.
【选自教材P51 习题2.8】
△ = 0
x1+x2= ,x1x2 = .
x1= x2=
(4)x2-4x-8=0
△ > 0
x1+x2= 4,x1x2 =-8 .
x1=
x2=
(3)3x2- x+1=0
3. 已知方程 5x2+kx-6 = 0 的一个根是 2,求它的另一个根
及 k 的值.
【选自教材P51 习题2.8】
x1+x2= ,
x1x2 = .
解:由题意,可得
k = -7.
∵ x1= 2,x2 = .
4. 如果一个三角形两边的长分别等于一元二次方程
x2-17x+66 = 0 的两个实数根,那么这个三角形的
第三边的长可能是 20 吗?为什么?
【选自教材P51 习题2.8】
解:由题意,可得 x1+x2 = 17,即两边长之和为 17,小于 20,所以这个三角形的第三边的长不可能是 20.
通过这节课的学习活动,你有什么收获?
课堂小结
2. 应用一元二次方程的根与系数关系时,首先要把已知方程化成一般形式.
3. 应用一元二次方程的根与系数关系时,要特别注意,方程有实根的条件,即在初中代数里,当且仅当b2-4ac ≥ 0 时,才能应用根与系数的关系.
1. 一元二次方程根与系数的关系是什么?
完成练习册本课时的习题。
课后作业
5 一元二次方程的根与系数的关系
2
北师版九年级上册
复习导入
1. 一元二次方程的一般形式?
ax2 + bx + c = 0 ( a≠0 )
2.一元二次方程有实数根的条件是什么?
△ = b2-4ac ≥ 0
3. 当△>0,△=0,△<0 根的情况如何?
复习导入
△ > 0 时,方程有两个不相等的实数根;
△ = 0 时,方程有两个相等的实数根;
△ < 0 时,方程没有实数根;
4. 一元二次方程的求根公式是什么?
复习导入
同学们,我们来做一个游戏,看谁能更快速的说出下列一元二次方程的两根和与两根积?
(1)x2-2x+1=0 (2)x2 - x-1=0 (3) 2x2-3x +1=0
探究新知
计算填表:
方程 x1 x2 x1+x2 x1x2
x2-2x+1=0
x2 - x-1=0
2x2-3x +1=0
1
1
2
1
-1
1
每个方程的两根之和与它的系数有什么关系?两根之积呢?
对于任何一个一元二次方程,这种关系都成立吗?与同伴交流。
一元二次方程 ax2+bx+c=0(a≠0)当b2-4ac ≥ 0 时有两个根:
x1+x2 =
x1x2 =
如果方程 ax2+bx+c=0(a≠0)有两根实数根x1,x2,那么
x1+x2 =
x1x2 =
例 利用根与系数的关系,求下列方程的两根之和、两根之积:
(1)x2 +7x +6 = 0 ; (2)2x2 - 3x -2 = 0 .
解: (1)这里 a = 1,b = 7,c = 6.
△ =b2-4ac = 72+4×1×6 = 49-24 = 25 > 0
∴方程有两个实数根.
设方程的两个实数根是x1,x2,那么.
x1+x2=-7, x1x2 = 6.
例 利用根与系数的关系,求下列方程的两根之和、两根之积:
(1)x2 +7x +6 = 0 ; (2)2x2 - 3x -2 = 0 .
(2)这里 a = 2,b = -3,c = -2.
△ =b2-4ac = (-3)2-4×2×(-2) = 9+16 = 25 > 0
∴方程有两个实数根.
设方程的两个实数根是x1,x2,那么.
x1+x2= , x1x2 = -1.
随堂练习
【选自教材P50 随堂练习】
利用根与系数的关系,求下列方程的两根之和、两根之积: (1)x2-3x-1=0; (2)3x2+2x-5=0.
解:(1)x1+x2=3, x1x2 = -1.
(2)x1+x2= , x1x2 = .
【选自教材P50 随堂练习】
2. 小明和小华分别求出了方程 9x2+6x-1=0 的根.
小明:x1 = x2 = ;小华:x1 = ,x2 = .
他们的答案正确吗?说说你的判断方法.
x1+x2= ,
x1x2 = .
解:由题意,可得
小明和小华求得的根与算式都不符合,
∴小明和小华的答案都不正确.
【选自教材P50 随堂练习】
3. 已知方程 x2- x-7=0 的一个根是 3 ,求它的另一个根.
解:x1x2 = -7.
x1 = 3.
x2 = .
达标检测
利用根与系数的关系,求下列方程的两根之和、两根之积:
(1)x(3x - 1)-1= 0; (2)(2x + 5) (x+1)= x + 7.
【选自教材P51 习题2.8】
解:(1)3x2-x-1=0.
x1+x2= ,x1x2 = .
(2)x2+3x-1=0.
x1+x2= -3,x1x2 = -1 .
2. 解下列方程:
(1)12x2+7x+1 = 0; (2)0.8x2 + x = 0.3.
(3)3x2+1= x; (4)(x+1)(x-3) = 2x+5.
【选自教材P51 习题2.8】
解:(1)
△ > 0
x1+x2= ,x1x2 = .
x1=
x2=
(2)
△ > 0
x1+x2= ,x1x2 = .
x1=
x2=
2. 解下列方程:
(1)12x2+7x+1 = 0; (2)0.8x2 + x = 0.3.
(3)3x2+1= x; (4)(x+1)(x-3) = 2x+5.
【选自教材P51 习题2.8】
△ = 0
x1+x2= ,x1x2 = .
x1= x2=
(4)x2-4x-8=0
△ > 0
x1+x2= 4,x1x2 =-8 .
x1=
x2=
(3)3x2- x+1=0
3. 已知方程 5x2+kx-6 = 0 的一个根是 2,求它的另一个根
及 k 的值.
【选自教材P51 习题2.8】
x1+x2= ,
x1x2 = .
解:由题意,可得
k = -7.
∵ x1= 2,x2 = .
4. 如果一个三角形两边的长分别等于一元二次方程
x2-17x+66 = 0 的两个实数根,那么这个三角形的
第三边的长可能是 20 吗?为什么?
【选自教材P51 习题2.8】
解:由题意,可得 x1+x2 = 17,即两边长之和为 17,小于 20,所以这个三角形的第三边的长不可能是 20.
通过这节课的学习活动,你有什么收获?
课堂小结
2. 应用一元二次方程的根与系数关系时,首先要把已知方程化成一般形式.
3. 应用一元二次方程的根与系数关系时,要特别注意,方程有实根的条件,即在初中代数里,当且仅当b2-4ac ≥ 0 时,才能应用根与系数的关系.
1. 一元二次方程根与系数的关系是什么?
完成练习册本课时的习题。
课后作业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
