【高效备课】北师大版九(上) 第2章 一元二次方程 6 应用一元二次方程 第1课时 利用一元二次方程解决几何问题 课件
文档属性
| 名称 | 【高效备课】北师大版九(上) 第2章 一元二次方程 6 应用一元二次方程 第1课时 利用一元二次方程解决几何问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:35:06 | ||
图片预览


文档简介
(共14张PPT)
利用一元二次方程解决几何问题
2
北师版九年级上册
情境导入
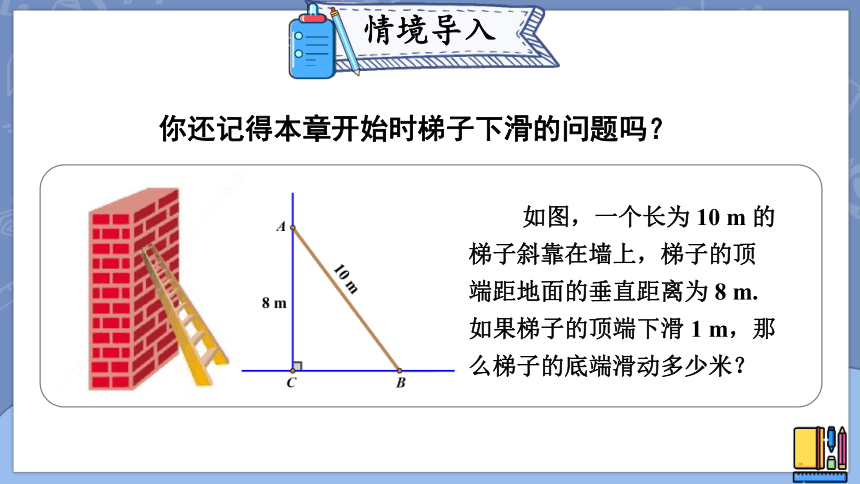
你还记得本章开始时梯子下滑的问题吗?
如图,一个长为 10 m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8 m.如果梯子的顶端下滑 1 m,那么梯子的底端滑动多少米?
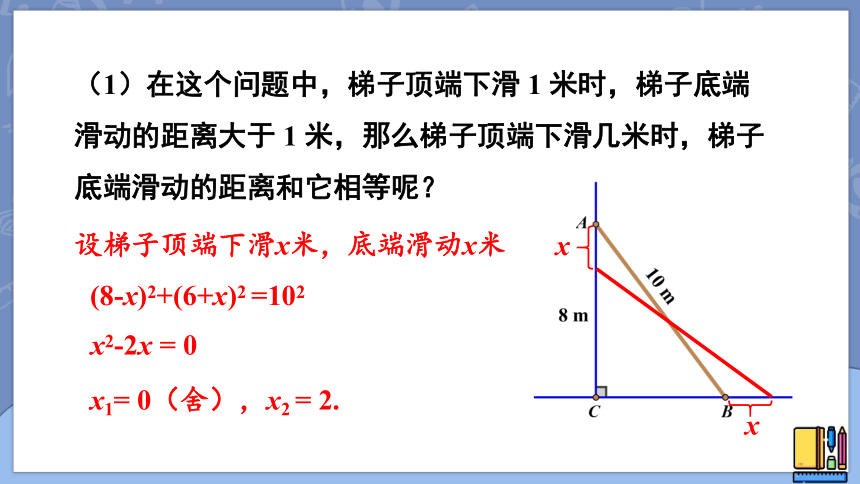
(1)在这个问题中,梯子顶端下滑 1 米时,梯子底端滑动的距离大于 1 米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
x
x
设梯子顶端下滑x米,底端滑动x米
(8-x)2+(6+x)2 =102
x2-2x = 0
x1= 0(舍),x2 = 2.
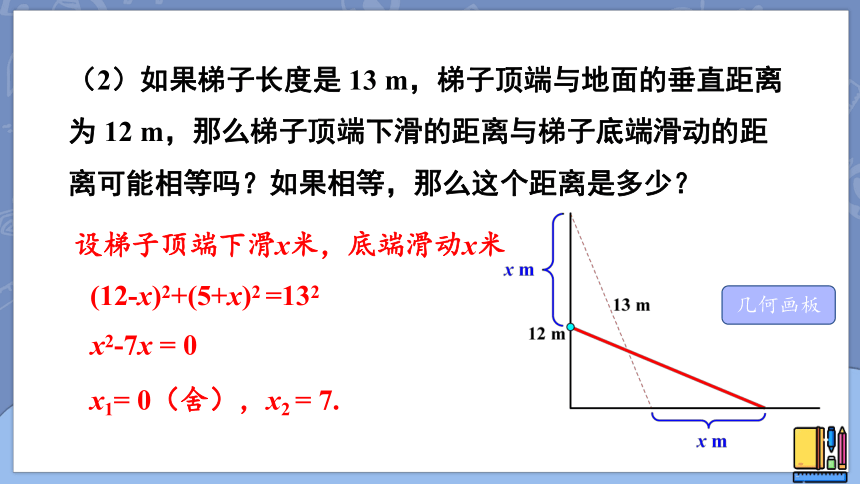
(2)如果梯子长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
设梯子顶端下滑x米,底端滑动x米
(12-x)2+(5+x)2 =132
x2-7x = 0
x1= 0(舍),x2 = 7.
几何画板
探究新知
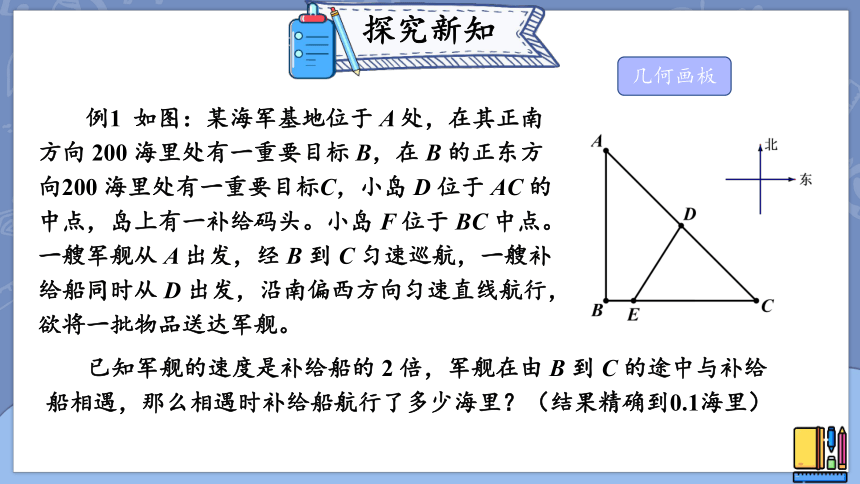
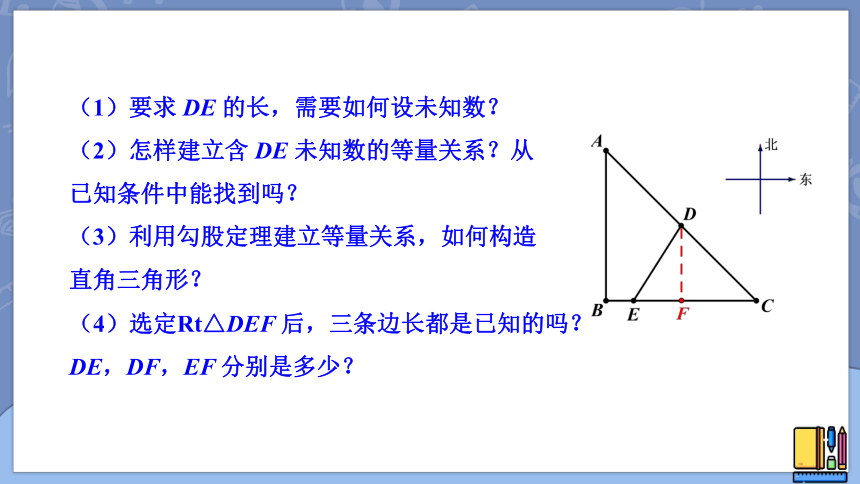
例1 如图:某海军基地位于 A 处,在其正南方向 200 海里处有一重要目标 B,在 B 的正东方向200 海里处有一重要目标C,小岛 D 位于 AC 的中点,岛上有一补给码头。小岛 F 位于 BC 中点。一艘军舰从 A 出发,经 B 到 C 匀速巡航,一艘补给船同时从 D 出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰。
已知军舰的速度是补给船的 2 倍,军舰在由 B 到 C 的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
几何画板
(1)要求 DE 的长,需要如何设未知数?
(2)怎样建立含 DE 未知数的等量关系?从已知条件中能找到吗?
(3)利用勾股定理建立等量关系,如何构造直角三角形?
(4)选定Rt△DEF 后,三条边长都是已知的吗?DE,DF,EF 分别是多少?
解: 连接 DF.
∵AD = CD,BF = CF,
∴DF 是△ABC 的中位线.
∴DF∥AB,且 DF = AB.
∵AB⊥BC,DF = 100 n mile,BF = 100 n mile.
设相遇时补给船航行了 x n mile,那么
DE = x nmile,AB + BE = 2x n mile,
EF = AB + BF-(AB + BE)=(300-2x)n mile.
在Rt△DEF 中,根据勾股定理可得方程
x2 = 1002 + (300-2x)2,
整理,得 3x2-1200x + 100 000 = 0.
解这个方程,得
所以,相遇时补给船大约航行了 118.4 n mile.
随堂练习
【选自教材P53 随堂练习】
《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲乙行各几何。”大意是说:已知甲、乙二人同时从同一地点出发,甲的速度为 7,乙的速度为 3。乙一直向东走,甲先向南走了 10 步,后又斜向北偏东方向走了一段后与乙相遇。那么相遇时,甲、乙各走了多远?
解:设所行时间为 t,则有 (3t)2 +102 = (7t-10)2,
解得 t1 = 0(舍去),t2 = .
∴甲走了 ×7 = (步),乙走了 ×3 = (步).
达标检测
【选自教材P53 习题2.9】
有这样一道阿拉伯古算题:有两笔钱,一多一少,其和等于 20,积等于 96,多的一笔钱被许诺赏给赛义德,那么赛义德得到多少钱?
解: 设较多的钱为 x.
由题意,可得 x(20-x)=96,解得 x1=12,x2=8 (舍去).
所以,赛义德得到的钱数为12.
如图:在 Rt△ACB 中,∠C = 90°,点 P、Q 同时由A、B 两点出发分别沿 AC、BC 方向向点 C 匀速移动,它们的速度都是 1 m/s,几秒后△PCQ 的面积为Rt△ACB 面积的一半?
解: 设经过 t s, △PCQ 面积为 Rt△ACB 面积的一半.
(8-t)(6-t)= ×6×8× ,
解得 t1=2,t2=12 (舍去).
所以,经过 2 s,△PCQ 面积为 Rt△ACB 面积的一半.
【选自教材P53 习题2.9】
如图,一条水渠的断面为梯形,已知断面的面积为 0.78 m2,上口比渠底宽 0.6,渠深比渠底少 0.4 m,求渠深.
【选自教材P53 习题2.9】
解:设渠深为 x m,则渠底为 (x+0.4) m.
S = ·[(x+0.4+0.6+x+0.4)]·x = 0.78,
解得 x1=-1.3(舍去),x2=0.6.
所以,渠深 0.6 m.
解: 设 t s 后 P ,Q 两点相距 15 cm.
由题意有 t2+(21-t)2=152,
解得 t1=9,t2=12.
所以,运动 9 s 或12 s 时,P ,Q 两点相距 15 cm.
如图,在Rt△ACB 中,∠C = 90°,AC = 30 cm,BC = 21 cm.动点 P 从点 C 出发,沿 CA 方向运动;动点 Q 同时从点 B 出发,沿 BC 方向运动. 如果动点 P,Q 的运动速度均为 1 cm/s,那么运动几秒时,它们相距 15 cm?.
【选自教材P54 习题2.9】
通过这节课的学习活动,你有什么收获?
课堂小结
完成练习册本课时的习题。
课后作业
利用一元二次方程解决几何问题
2
北师版九年级上册
情境导入
你还记得本章开始时梯子下滑的问题吗?
如图,一个长为 10 m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8 m.如果梯子的顶端下滑 1 m,那么梯子的底端滑动多少米?
(1)在这个问题中,梯子顶端下滑 1 米时,梯子底端滑动的距离大于 1 米,那么梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
x
x
设梯子顶端下滑x米,底端滑动x米
(8-x)2+(6+x)2 =102
x2-2x = 0
x1= 0(舍),x2 = 2.
(2)如果梯子长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
设梯子顶端下滑x米,底端滑动x米
(12-x)2+(5+x)2 =132
x2-7x = 0
x1= 0(舍),x2 = 7.
几何画板
探究新知
例1 如图:某海军基地位于 A 处,在其正南方向 200 海里处有一重要目标 B,在 B 的正东方向200 海里处有一重要目标C,小岛 D 位于 AC 的中点,岛上有一补给码头。小岛 F 位于 BC 中点。一艘军舰从 A 出发,经 B 到 C 匀速巡航,一艘补给船同时从 D 出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰。
已知军舰的速度是补给船的 2 倍,军舰在由 B 到 C 的途中与补给船相遇,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)
几何画板
(1)要求 DE 的长,需要如何设未知数?
(2)怎样建立含 DE 未知数的等量关系?从已知条件中能找到吗?
(3)利用勾股定理建立等量关系,如何构造直角三角形?
(4)选定Rt△DEF 后,三条边长都是已知的吗?DE,DF,EF 分别是多少?
解: 连接 DF.
∵AD = CD,BF = CF,
∴DF 是△ABC 的中位线.
∴DF∥AB,且 DF = AB.
∵AB⊥BC,DF = 100 n mile,BF = 100 n mile.
设相遇时补给船航行了 x n mile,那么
DE = x nmile,AB + BE = 2x n mile,
EF = AB + BF-(AB + BE)=(300-2x)n mile.
在Rt△DEF 中,根据勾股定理可得方程
x2 = 1002 + (300-2x)2,
整理,得 3x2-1200x + 100 000 = 0.
解这个方程,得
所以,相遇时补给船大约航行了 118.4 n mile.
随堂练习
【选自教材P53 随堂练习】
《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会,问甲乙行各几何。”大意是说:已知甲、乙二人同时从同一地点出发,甲的速度为 7,乙的速度为 3。乙一直向东走,甲先向南走了 10 步,后又斜向北偏东方向走了一段后与乙相遇。那么相遇时,甲、乙各走了多远?
解:设所行时间为 t,则有 (3t)2 +102 = (7t-10)2,
解得 t1 = 0(舍去),t2 = .
∴甲走了 ×7 = (步),乙走了 ×3 = (步).
达标检测
【选自教材P53 习题2.9】
有这样一道阿拉伯古算题:有两笔钱,一多一少,其和等于 20,积等于 96,多的一笔钱被许诺赏给赛义德,那么赛义德得到多少钱?
解: 设较多的钱为 x.
由题意,可得 x(20-x)=96,解得 x1=12,x2=8 (舍去).
所以,赛义德得到的钱数为12.
如图:在 Rt△ACB 中,∠C = 90°,点 P、Q 同时由A、B 两点出发分别沿 AC、BC 方向向点 C 匀速移动,它们的速度都是 1 m/s,几秒后△PCQ 的面积为Rt△ACB 面积的一半?
解: 设经过 t s, △PCQ 面积为 Rt△ACB 面积的一半.
(8-t)(6-t)= ×6×8× ,
解得 t1=2,t2=12 (舍去).
所以,经过 2 s,△PCQ 面积为 Rt△ACB 面积的一半.
【选自教材P53 习题2.9】
如图,一条水渠的断面为梯形,已知断面的面积为 0.78 m2,上口比渠底宽 0.6,渠深比渠底少 0.4 m,求渠深.
【选自教材P53 习题2.9】
解:设渠深为 x m,则渠底为 (x+0.4) m.
S = ·[(x+0.4+0.6+x+0.4)]·x = 0.78,
解得 x1=-1.3(舍去),x2=0.6.
所以,渠深 0.6 m.
解: 设 t s 后 P ,Q 两点相距 15 cm.
由题意有 t2+(21-t)2=152,
解得 t1=9,t2=12.
所以,运动 9 s 或12 s 时,P ,Q 两点相距 15 cm.
如图,在Rt△ACB 中,∠C = 90°,AC = 30 cm,BC = 21 cm.动点 P 从点 C 出发,沿 CA 方向运动;动点 Q 同时从点 B 出发,沿 BC 方向运动. 如果动点 P,Q 的运动速度均为 1 cm/s,那么运动几秒时,它们相距 15 cm?.
【选自教材P54 习题2.9】
通过这节课的学习活动,你有什么收获?
课堂小结
完成练习册本课时的习题。
课后作业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
