【高效备课】北师大版九(上) 第2章 一元二次方程 6 应用一元二次方程 第2课时 利用一元二次方程解决经济问题 课件
文档属性
| 名称 | 【高效备课】北师大版九(上) 第2章 一元二次方程 6 应用一元二次方程 第2课时 利用一元二次方程解决经济问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:35:06 | ||
图片预览






文档简介
(共15张PPT)
利用一元二次方程解决经济问题
2
北师版九年级上册
知识回顾
请同学们回忆并回答与利润相关的知识
利润 =( )- 进价
售价
售价 = 标价×折扣
9 折要乘以 90% 或 0.9 或 ,那么 x 折呢?
探究新知
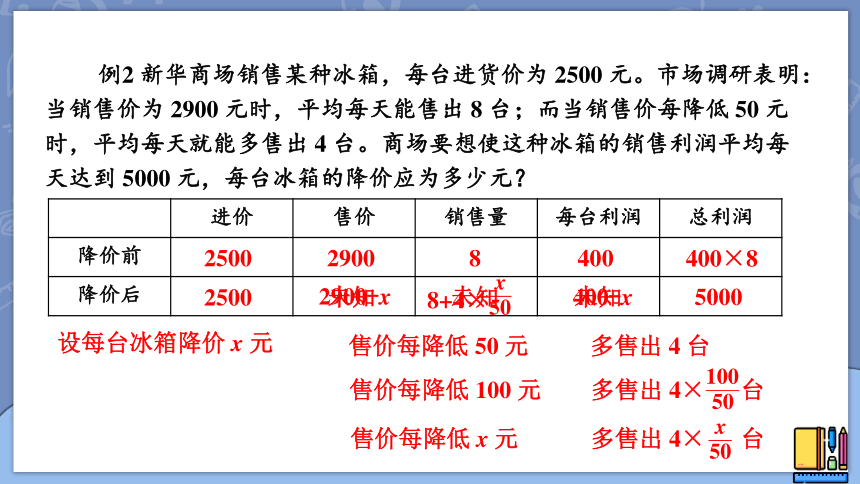
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
分析基本数量关系
售价 - 进价 = 利润
每台利润 × 每天的销售量 = 每天的总利润
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
进价 售价 销售量 每台利润 总利润
降价前
降价后
2500
2900
8
400
400×8
2500
未知
未知
未知
5000
设每台冰箱降价 x 元
售价每降低 50 元
多售出 4 台
售价每降低 100 元
多售出 4× 台
售价每降低 x 元
多售出 4× 台
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
进价 售价 销售量 每台利润 总利润
降价前
降价后
2500
2900
8
400
400×8
2500
未知
未知
未知
5000
设每台冰箱降价 x 元
售价每降低 50 元
多售出 4 台
售价每降低 100 元
多售出 4× 台
售价每降低 x 元
多售出 4× 台
2900-x
8+4×
400-x
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
解:设每台冰箱降价 x 元,根据题意,得
8+4×
( 2900-x -2500)( ) = 5000
解这个方程,得
x1 = x2 = 150.
2900-150 = 2750
所以,每台冰箱应定价为 2750 元.
某商场将进货价为 30 元的台灯以 40 元售出,平均每月能售出 600 个。调查发现:售价在 40 元至 60 元范围内,这种台灯的售价每上涨 1 元,其销售量就将减少 10 个.为了实现平均每月 10 000 元的销售利润,这种台灯的售价应定为多少?这时应购进台灯多少个?
解:设这种台灯售价上涨 x 元,根据题意,得
(40+x-30)(600-10x) = 10 000
解这个方程,得
x1 = 10.
x2 = 40(舍).
售价为:40+x = 40+10 = 50(元)
应购置台灯:600-10x = 600-10×10 = 500(个)
利用方程解决实际问题得关键和步骤是什么?
关键:寻找等量关系
步骤:其一是整体地、系统地审清问题;
其二是把握问题中的“相等关系”;
其三是正确求解方程并检验解的合理性。
随堂练习
【选自教材P55 随堂练习】
某批发市场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出 500 张,每张赢利 0.3 元. 为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价 0.05 元,那么平均每天可多售出 200 张. 摊主要想平均每天赢利 180 元,每张贺年卡应降价多少元?
解:设每张贺卡应降价 x 元.
(0.3-x) ( ×200+500) =180,
解得 x1=0.1,x2= .
又∵摊主想尽快减少库存.
∴减得越多,卖得越多.
在盈利相同的情况下选择降价 0.1 元更合适.
达标检测
【选自教材P55 习题2.10】
某种服装,平均每天可销售 20 件,每件赢利 44 元. 在每件降价幅度不超过 10 元的情况下,若每件降价 1 元,则每天可多售 5 件.如果每天要赢利 1600 元,每件应降价多少元?
解: 设每件应降价 x 元.
(5x+20)(44-x)=1600,解得: x1=4,x2=36 (舍去)
所以,每件应降价 4 元.
一个农业合作社以 64000 元的成本收获了某种农产品 80t,目前可以以 1200 元/t 的价格售出.如果储藏起来,每星期会损失 2t,且每星期需支付各种费用 1600 元,但同时每星期每吨的价格将上涨 200 元. 那么,储藏多少个星期出售这批农产品可获利 122000 元?
【选自教材P55 习题2.10】
解: 设储藏 x 个星期出售这批农产品可获利 122 000 元.
(1200+200x)(80-2x)-1600x = 122000 +64000,
解得 x1=x2=15.
所以,储藏 15 个星期出售这批农产品可获利 122000元.
【选自教材P55 习题2.10】
我国2019年并网太阳能发电装机容量约为2亿kW,经过两年努力,我国2021年并网太阳能发电装机容量约为3亿kW,求我国这两年并网太阳能发电装机容量的年均增长率(结果精确到 1%).
解: 设我国这两年并网太阳能发电装机容量的年均增长率为 x.
2(1+x)2 = 3,解得 x1= (舍去),
x2= ≈ 22.5%.
所以,我国这两年并网太阳能发电装机容量的年均增长率为 22.5%.
【选自教材P55 习题2.10】
某公司今年 10 月的营业额为 2500 万元,按计划第四季度的总营业额要达到 9100 万元,求该公司 11,12 两个月营业额的月均增长率.
解:设该公司 11,12 两个月营业额的月均增长率为 x.
2500+2500(1+x)+2500(1+x)2=9100,
解得 x1=0.2=20%,x2=-3.2(舍去).
故该公司 11,12 两个月营业额的月均增长率为 20%.
通过这节课的学习活动,你有什么收获?
课堂小结
完成练习册本课时的习题。
课后作业
利用一元二次方程解决经济问题
2
北师版九年级上册
知识回顾
请同学们回忆并回答与利润相关的知识
利润 =( )- 进价
售价
售价 = 标价×折扣
9 折要乘以 90% 或 0.9 或 ,那么 x 折呢?
探究新知
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
分析基本数量关系
售价 - 进价 = 利润
每台利润 × 每天的销售量 = 每天的总利润
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
进价 售价 销售量 每台利润 总利润
降价前
降价后
2500
2900
8
400
400×8
2500
未知
未知
未知
5000
设每台冰箱降价 x 元
售价每降低 50 元
多售出 4 台
售价每降低 100 元
多售出 4× 台
售价每降低 x 元
多售出 4× 台
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
进价 售价 销售量 每台利润 总利润
降价前
降价后
2500
2900
8
400
400×8
2500
未知
未知
未知
5000
设每台冰箱降价 x 元
售价每降低 50 元
多售出 4 台
售价每降低 100 元
多售出 4× 台
售价每降低 x 元
多售出 4× 台
2900-x
8+4×
400-x
例2 新华商场销售某种冰箱,每台进货价为 2500 元。市场调研表明:当销售价为 2900 元时,平均每天能售出 8 台;而当销售价每降低 50 元时,平均每天就能多售出 4 台。商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的降价应为多少元?
解:设每台冰箱降价 x 元,根据题意,得
8+4×
( 2900-x -2500)( ) = 5000
解这个方程,得
x1 = x2 = 150.
2900-150 = 2750
所以,每台冰箱应定价为 2750 元.
某商场将进货价为 30 元的台灯以 40 元售出,平均每月能售出 600 个。调查发现:售价在 40 元至 60 元范围内,这种台灯的售价每上涨 1 元,其销售量就将减少 10 个.为了实现平均每月 10 000 元的销售利润,这种台灯的售价应定为多少?这时应购进台灯多少个?
解:设这种台灯售价上涨 x 元,根据题意,得
(40+x-30)(600-10x) = 10 000
解这个方程,得
x1 = 10.
x2 = 40(舍).
售价为:40+x = 40+10 = 50(元)
应购置台灯:600-10x = 600-10×10 = 500(个)
利用方程解决实际问题得关键和步骤是什么?
关键:寻找等量关系
步骤:其一是整体地、系统地审清问题;
其二是把握问题中的“相等关系”;
其三是正确求解方程并检验解的合理性。
随堂练习
【选自教材P55 随堂练习】
某批发市场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出 500 张,每张赢利 0.3 元. 为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价 0.05 元,那么平均每天可多售出 200 张. 摊主要想平均每天赢利 180 元,每张贺年卡应降价多少元?
解:设每张贺卡应降价 x 元.
(0.3-x) ( ×200+500) =180,
解得 x1=0.1,x2= .
又∵摊主想尽快减少库存.
∴减得越多,卖得越多.
在盈利相同的情况下选择降价 0.1 元更合适.
达标检测
【选自教材P55 习题2.10】
某种服装,平均每天可销售 20 件,每件赢利 44 元. 在每件降价幅度不超过 10 元的情况下,若每件降价 1 元,则每天可多售 5 件.如果每天要赢利 1600 元,每件应降价多少元?
解: 设每件应降价 x 元.
(5x+20)(44-x)=1600,解得: x1=4,x2=36 (舍去)
所以,每件应降价 4 元.
一个农业合作社以 64000 元的成本收获了某种农产品 80t,目前可以以 1200 元/t 的价格售出.如果储藏起来,每星期会损失 2t,且每星期需支付各种费用 1600 元,但同时每星期每吨的价格将上涨 200 元. 那么,储藏多少个星期出售这批农产品可获利 122000 元?
【选自教材P55 习题2.10】
解: 设储藏 x 个星期出售这批农产品可获利 122 000 元.
(1200+200x)(80-2x)-1600x = 122000 +64000,
解得 x1=x2=15.
所以,储藏 15 个星期出售这批农产品可获利 122000元.
【选自教材P55 习题2.10】
我国2019年并网太阳能发电装机容量约为2亿kW,经过两年努力,我国2021年并网太阳能发电装机容量约为3亿kW,求我国这两年并网太阳能发电装机容量的年均增长率(结果精确到 1%).
解: 设我国这两年并网太阳能发电装机容量的年均增长率为 x.
2(1+x)2 = 3,解得 x1= (舍去),
x2= ≈ 22.5%.
所以,我国这两年并网太阳能发电装机容量的年均增长率为 22.5%.
【选自教材P55 习题2.10】
某公司今年 10 月的营业额为 2500 万元,按计划第四季度的总营业额要达到 9100 万元,求该公司 11,12 两个月营业额的月均增长率.
解:设该公司 11,12 两个月营业额的月均增长率为 x.
2500+2500(1+x)+2500(1+x)2=9100,
解得 x1=0.2=20%,x2=-3.2(舍去).
故该公司 11,12 两个月营业额的月均增长率为 20%.
通过这节课的学习活动,你有什么收获?
课堂小结
完成练习册本课时的习题。
课后作业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
