【高效备课】北师大版九(上) 第4章 图形的相似 1 成比例线段 第1课时 线段的比和比例的基本性质 课件
文档属性
| 名称 | 【高效备课】北师大版九(上) 第4章 图形的相似 1 成比例线段 第1课时 线段的比和比例的基本性质 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:35:06 | ||
图片预览






文档简介
(共23张PPT)
线段的比和比例的基本性质
北师版九年级上册
情景导入
实际生活中,我们经常会看到许多形状相同的图片。
新课导入
如图,用同一张底片洗出的不同尺寸的照片中,汽车的形状还相同吗?
如图,几个足球的形状相同吗?他们的大小呢?
新课导入
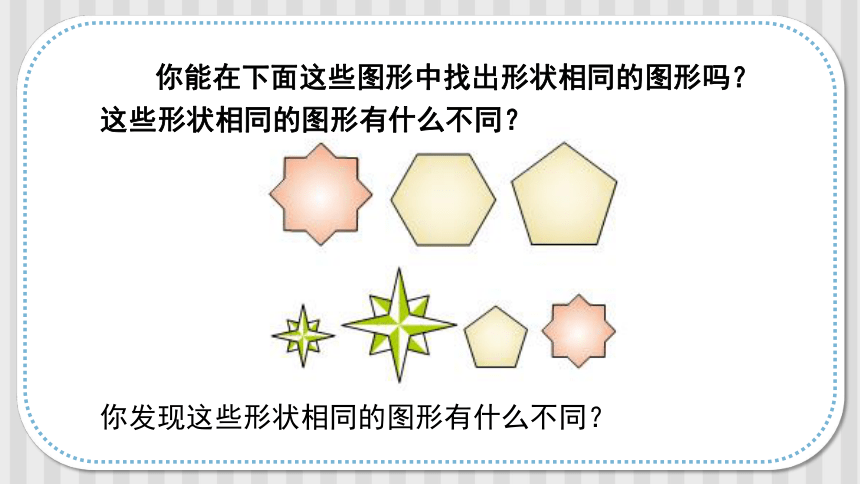
你能在下面这些图形中找出形状相同的图形吗?这些形状相同的图形有什么不同?
你发现这些形状相同的图形有什么不同?
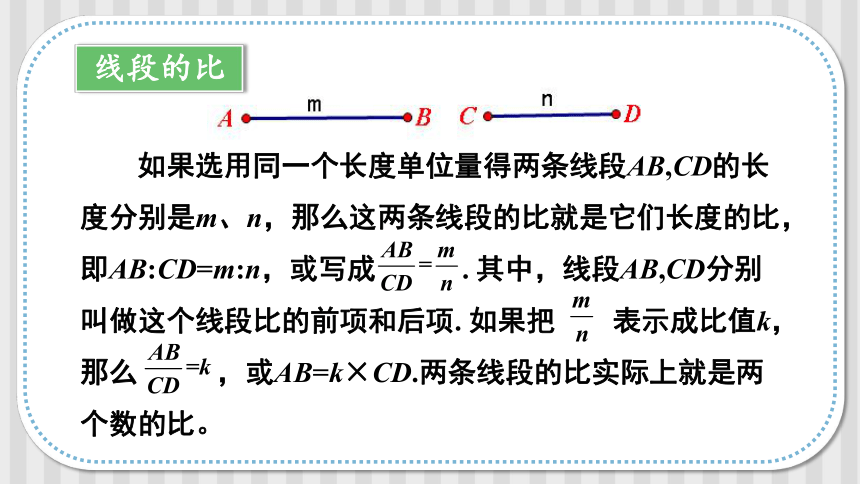
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n,那么这两条线段的比就是它们长度的比,即AB:CD=m:n,或写成 . 其中,线段AB,CD分别叫做这个线段比的前项和后项. 如果把 表示成比值k,那么 ,或AB=k×CD.两条线段的比实际上就是两个数的比。
线段的比
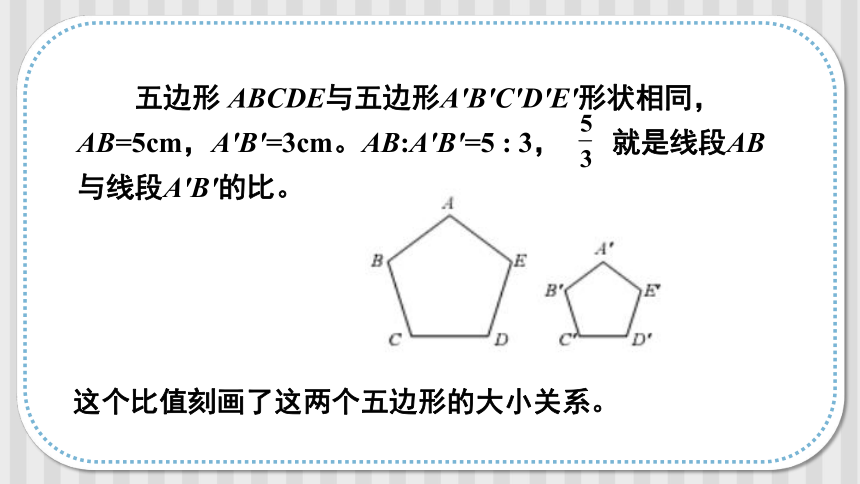
五边形 ABCDE与五边形A′B′C′D′E′形状相同,AB=5cm,A′B′=3cm。AB:A′B′=5 : 3, 就是线段AB与线段A′B′的比。
这个比值刻画了这两个五边形的大小关系。
两条线段长度的比与所采用的长度单位有没有关系?
想一想
如图,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,CD,EH,EF的长度分别是多少?分别计算 值。
你发现了什么?
做一做
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
上图中AB,EH,AD,EF是成比例线段,AB,AD,EF,EH也是成比例线段。
成比例线段
跟踪练习
1. 判断下列四条线段是否成比例
答: (1)a,b,c,d 不成比例,但a,d,b,c成比例.
(2)不成比例.
(3)不成比例.
(4)a,b,c,d成比例.
不知你是否注意到:比例与叙述的顺序有关
如果 a,b,c,d 四个数成比例,即 ,那么 ad = bc 吗?反过来如果 ad = bc,那么a,b,c,d 四个数成比例吗?
议一议
如果 = ,那么 ad = bc .
如果 ad = bc ( a,b,c,d 都不等于0 ),那么 = .
比例的基本性质
如图,一块矩形绸布的长AB = a m, AD = 1m,按照图中所示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么 a 的值应当是多少?
例1
1.你知道地图比例尺的含义吗?生活中还有哪些利用线段比的事例?
达标检测
【选自教材P79 随堂练习】
梯子
黄金分割
2.一条线段的长度是另一条线段长度的5倍,
求这两条线段的比.
5:1
达标检测
【选自教材P79 随堂练习】
3. a,b,c,d是成比例线段,其中 a = 3 cm,
b = 2 cm, c = 6 cm,求线段 d 的长.
解:已知a,b, c, d是成比例线段,
根据比例线段的定义得: ad = cb,
代入 a = 3 , b = 2 , c = 6,
解得: d = 4,则 d = 4 cm .
故答案为: 4
【选自教材P79 随堂练习】
达标检测
达标检测
4.在△ABC中,∠B = 90°,AB = BC = 10 cm;在△DEF中, ED = EF = 12 cm,DF= 8 cm,求AB与EF之比、AC与DF之比。
解:由题意,可得AC= cm,
则 , .
【选自教材P79 习题4.1】
达标检测
5.如图,在△ABC中,D,E 分别是 AB 和 AC 上的点,AB= 12 cm,AE = 6 cm,EC = 5 cm,且 ,
求AD的长.
解:由题意,可得AC= cm,
则 , .
【选自教材P79 习题4.1】
6.如图,将一张矩形纸片沿它的长边对折(EF为折痕),得到两个全等的小矩形。如果小矩形长边与短边的比等于原来矩形长边与短边的比,那么原来矩形的长边与短边的比是多少
【选自教材P79 习题4.1】
达标检测
解:设小矩形的长边为x短边为y,则原来矩形的长边为2y,短边为x由题意得:x:y=2y:x
即: 2y2 = x2 解得: y= x
所以:2y:x=2× x:x=
即:原来矩形长边与短边的比是 。
达标检测
完成练习册本课时的习题。
课后作业
线段的比和比例的基本性质
北师版九年级上册
情景导入
实际生活中,我们经常会看到许多形状相同的图片。
新课导入
如图,用同一张底片洗出的不同尺寸的照片中,汽车的形状还相同吗?
如图,几个足球的形状相同吗?他们的大小呢?
新课导入
你能在下面这些图形中找出形状相同的图形吗?这些形状相同的图形有什么不同?
你发现这些形状相同的图形有什么不同?
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n,那么这两条线段的比就是它们长度的比,即AB:CD=m:n,或写成 . 其中,线段AB,CD分别叫做这个线段比的前项和后项. 如果把 表示成比值k,那么 ,或AB=k×CD.两条线段的比实际上就是两个数的比。
线段的比
五边形 ABCDE与五边形A′B′C′D′E′形状相同,AB=5cm,A′B′=3cm。AB:A′B′=5 : 3, 就是线段AB与线段A′B′的比。
这个比值刻画了这两个五边形的大小关系。
两条线段长度的比与所采用的长度单位有没有关系?
想一想
如图,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,CD,EH,EF的长度分别是多少?分别计算 值。
你发现了什么?
做一做
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
上图中AB,EH,AD,EF是成比例线段,AB,AD,EF,EH也是成比例线段。
成比例线段
跟踪练习
1. 判断下列四条线段是否成比例
答: (1)a,b,c,d 不成比例,但a,d,b,c成比例.
(2)不成比例.
(3)不成比例.
(4)a,b,c,d成比例.
不知你是否注意到:比例与叙述的顺序有关
如果 a,b,c,d 四个数成比例,即 ,那么 ad = bc 吗?反过来如果 ad = bc,那么a,b,c,d 四个数成比例吗?
议一议
如果 = ,那么 ad = bc .
如果 ad = bc ( a,b,c,d 都不等于0 ),那么 = .
比例的基本性质
如图,一块矩形绸布的长AB = a m, AD = 1m,按照图中所示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即 ,那么 a 的值应当是多少?
例1
1.你知道地图比例尺的含义吗?生活中还有哪些利用线段比的事例?
达标检测
【选自教材P79 随堂练习】
梯子
黄金分割
2.一条线段的长度是另一条线段长度的5倍,
求这两条线段的比.
5:1
达标检测
【选自教材P79 随堂练习】
3. a,b,c,d是成比例线段,其中 a = 3 cm,
b = 2 cm, c = 6 cm,求线段 d 的长.
解:已知a,b, c, d是成比例线段,
根据比例线段的定义得: ad = cb,
代入 a = 3 , b = 2 , c = 6,
解得: d = 4,则 d = 4 cm .
故答案为: 4
【选自教材P79 随堂练习】
达标检测
达标检测
4.在△ABC中,∠B = 90°,AB = BC = 10 cm;在△DEF中, ED = EF = 12 cm,DF= 8 cm,求AB与EF之比、AC与DF之比。
解:由题意,可得AC= cm,
则 , .
【选自教材P79 习题4.1】
达标检测
5.如图,在△ABC中,D,E 分别是 AB 和 AC 上的点,AB= 12 cm,AE = 6 cm,EC = 5 cm,且 ,
求AD的长.
解:由题意,可得AC= cm,
则 , .
【选自教材P79 习题4.1】
6.如图,将一张矩形纸片沿它的长边对折(EF为折痕),得到两个全等的小矩形。如果小矩形长边与短边的比等于原来矩形长边与短边的比,那么原来矩形的长边与短边的比是多少
【选自教材P79 习题4.1】
达标检测
解:设小矩形的长边为x短边为y,则原来矩形的长边为2y,短边为x由题意得:x:y=2y:x
即: 2y2 = x2 解得: y= x
所以:2y:x=2× x:x=
即:原来矩形长边与短边的比是 。
达标检测
完成练习册本课时的习题。
课后作业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
