【高效备课】北师大版九(上) 第3章 概率的进一步认识 回顾与思考 课件
文档属性
| 名称 | 【高效备课】北师大版九(上) 第3章 概率的进一步认识 回顾与思考 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:35:06 | ||
图片预览





文档简介
(共15张PPT)
回顾与思考
3
北师版九年级上册
复习导入
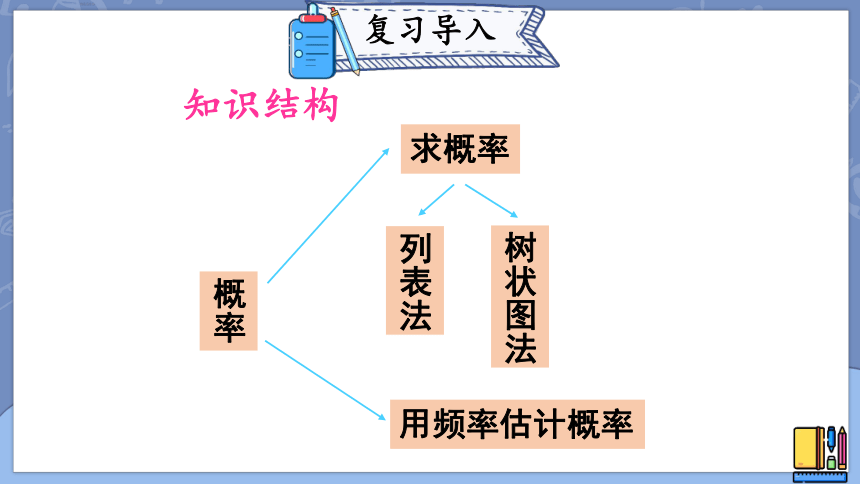
知识结构
概率
列表法
树状图法
求概率
用频率估计概率
1.用树状图或表格求概率.
复习导入
回顾:用树状图或表格求概率时应注意什么情况?
2.用频率估计概率.
如何用频率估计概率?
复习导入
核心考点训练
考点一 用列表格或画树状图求概率
考点二 用频率估计概率
1.某个事件发生的概率是 ,这意味着在两次重复试验中该事件必有一次发生吗
2.你能用试验的方法估计哪些事件发生的概率 举例说明.
3.有时通过试验的方法估计一个事件发生的概率有一定的难度,你能否通过模拟试验估计该事件发生的概率
4.你掌握了哪些求概率的方法 举例说明.
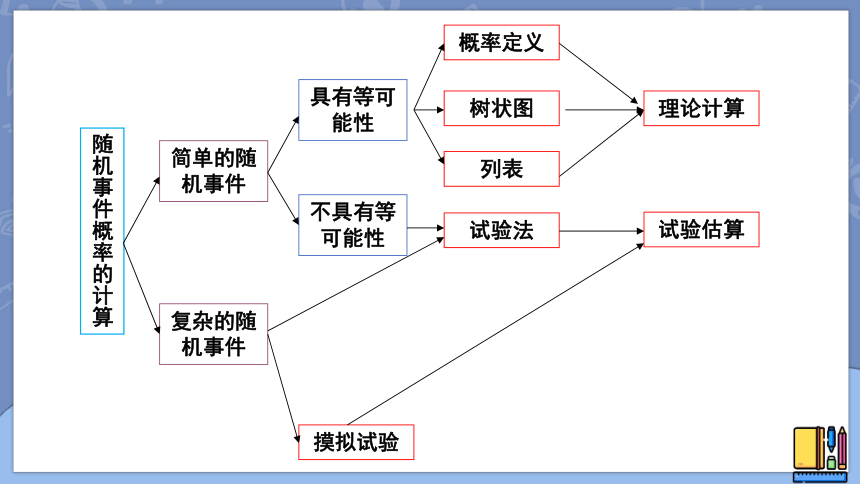
随机事件概率的计算
简单的随机事件
复杂的随机事件
具有等可能性
不具有等可能性
树状图
列表
试验法
摸拟试验
理论计算
试验估算
概率定义
用概率的意义求概率解决实际问题
1.在有一个10万人的小镇,随机调查了2000人,其中有250人看某电视台的早间新闻.在该镇随便问一个人,他看该电视台早间新闻的概率大约是多少
【选自教材P72 复习题 知识技能】
解:根据概率的意义,可以认为其概率大约等于
=0.125
等可能性,用树状图或表格求概率
2.(1)连掷两枚骰子,它们的点数相同的概率是多少
(2)转动如图所示的转盘(转盘被分成面积相等的六个扇形)两次,两次所得的颜色相同的概率是多少
(3)某口袋装有编号为 1~6 的六个球(除编号外都相同),先从中摸出一个球,将它放回口袋中,再摸一次,
两次摸到的球相同的概率是多少
白
红
蓝
黑
黄
绿
【选自教材P72 复习题 知识技能】
(4)小明认为,上面几个求概率的问题本质上是相同的,你同意他的观点吗?
白
红
蓝
黑
黄
绿
有放回摸拟试验用树状图和表格求概率
3.一个密码锁的密码由四个数字组成,每个数字都是0-9这十个数字中的一个,只有当四个数字与所设定的密码相同时,才能将锁打开.粗心的小明忘了其中中间的两个数字,他一次就能打开该锁的概率是多少
【选自教材P72 复习题 知识技能】
解:其概率为 . 第一次从0-9这10个数字中抽取1个数字,其概率为 ;第二次仍从0-9中抽取每二个数字,其概率仍为 .故概率为 .
用树状图和表格求概率
4.用如图所示的两个转盘进行配“紫色”游戏,其概率是多少
白
蓝
红
黄
绿
蓝
红
【选自教材P73 复习题 数学理解】
有放回摸拟试验用树状图和表格求概率
5.某种“15选5”的彩票的获奖号码是从1-15这15个数字中选择5个数字(可以重复),若彩民所选择的5个数字与获奖号码相同,即可获得特等奖.
小明观察了最近100期获奖号码,发现其中竟有51期有重号(同一期获奖号码中有2个或2个以上的数字相同),66期有连号(同一期获奖号码中有2个或2个以上的数字相邻).他认为,获奖号码中不应该有这么多重号或连号,获奖号码不可能是随机产生的,有失公允.
小明的观点有道理吗 重号的概率大约是多少 利用计算器摸拟试验估计重号的概率.
用树状图和表格求概率
6.小明和小亮用如图所示的两个转盘(每个转盘被分成五个面积相等的扇形)做游戏,转动两个转盘各一次.
(1)若两次数字之和为6,7或8,则小明胜,否则小亮胜.这个游戏对双方公平吗 说说你的理由.
(2)若两次数字之和为奇数,则小明胜;
若两次数字之和为偶数,则小亮胜.
这个游戏对双方公平吗 说说你的理由.
1
2
5
3
4
2
【选自教材P73 复习题 数学理解】
3
4
5
6
2
A盘
B盘
用试验的方法求概率
*7.如图,地面上铺满了正方形的地板砖(40cm×40cm),现在向这一地面上抛掷半径为5cm的圆碟,圆碟与地砖间的间隙相交的概率大约是多少 具体做做看.
【选自教材P74 复习题 问题解决】
课堂小结
概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策.
从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.
回顾与思考
3
北师版九年级上册
复习导入
知识结构
概率
列表法
树状图法
求概率
用频率估计概率
1.用树状图或表格求概率.
复习导入
回顾:用树状图或表格求概率时应注意什么情况?
2.用频率估计概率.
如何用频率估计概率?
复习导入
核心考点训练
考点一 用列表格或画树状图求概率
考点二 用频率估计概率
1.某个事件发生的概率是 ,这意味着在两次重复试验中该事件必有一次发生吗
2.你能用试验的方法估计哪些事件发生的概率 举例说明.
3.有时通过试验的方法估计一个事件发生的概率有一定的难度,你能否通过模拟试验估计该事件发生的概率
4.你掌握了哪些求概率的方法 举例说明.
随机事件概率的计算
简单的随机事件
复杂的随机事件
具有等可能性
不具有等可能性
树状图
列表
试验法
摸拟试验
理论计算
试验估算
概率定义
用概率的意义求概率解决实际问题
1.在有一个10万人的小镇,随机调查了2000人,其中有250人看某电视台的早间新闻.在该镇随便问一个人,他看该电视台早间新闻的概率大约是多少
【选自教材P72 复习题 知识技能】
解:根据概率的意义,可以认为其概率大约等于
=0.125
等可能性,用树状图或表格求概率
2.(1)连掷两枚骰子,它们的点数相同的概率是多少
(2)转动如图所示的转盘(转盘被分成面积相等的六个扇形)两次,两次所得的颜色相同的概率是多少
(3)某口袋装有编号为 1~6 的六个球(除编号外都相同),先从中摸出一个球,将它放回口袋中,再摸一次,
两次摸到的球相同的概率是多少
白
红
蓝
黑
黄
绿
【选自教材P72 复习题 知识技能】
(4)小明认为,上面几个求概率的问题本质上是相同的,你同意他的观点吗?
白
红
蓝
黑
黄
绿
有放回摸拟试验用树状图和表格求概率
3.一个密码锁的密码由四个数字组成,每个数字都是0-9这十个数字中的一个,只有当四个数字与所设定的密码相同时,才能将锁打开.粗心的小明忘了其中中间的两个数字,他一次就能打开该锁的概率是多少
【选自教材P72 复习题 知识技能】
解:其概率为 . 第一次从0-9这10个数字中抽取1个数字,其概率为 ;第二次仍从0-9中抽取每二个数字,其概率仍为 .故概率为 .
用树状图和表格求概率
4.用如图所示的两个转盘进行配“紫色”游戏,其概率是多少
白
蓝
红
黄
绿
蓝
红
【选自教材P73 复习题 数学理解】
有放回摸拟试验用树状图和表格求概率
5.某种“15选5”的彩票的获奖号码是从1-15这15个数字中选择5个数字(可以重复),若彩民所选择的5个数字与获奖号码相同,即可获得特等奖.
小明观察了最近100期获奖号码,发现其中竟有51期有重号(同一期获奖号码中有2个或2个以上的数字相同),66期有连号(同一期获奖号码中有2个或2个以上的数字相邻).他认为,获奖号码中不应该有这么多重号或连号,获奖号码不可能是随机产生的,有失公允.
小明的观点有道理吗 重号的概率大约是多少 利用计算器摸拟试验估计重号的概率.
用树状图和表格求概率
6.小明和小亮用如图所示的两个转盘(每个转盘被分成五个面积相等的扇形)做游戏,转动两个转盘各一次.
(1)若两次数字之和为6,7或8,则小明胜,否则小亮胜.这个游戏对双方公平吗 说说你的理由.
(2)若两次数字之和为奇数,则小明胜;
若两次数字之和为偶数,则小亮胜.
这个游戏对双方公平吗 说说你的理由.
1
2
5
3
4
2
【选自教材P73 复习题 数学理解】
3
4
5
6
2
A盘
B盘
用试验的方法求概率
*7.如图,地面上铺满了正方形的地板砖(40cm×40cm),现在向这一地面上抛掷半径为5cm的圆碟,圆碟与地砖间的间隙相交的概率大约是多少 具体做做看.
【选自教材P74 复习题 问题解决】
课堂小结
概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策.
从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
