【高效备课】北师大版九(上) 第4章 图形的相似 4 探索三角形相似的条件 第4课时 黄金分割 课件
文档属性
| 名称 | 【高效备课】北师大版九(上) 第4章 图形的相似 4 探索三角形相似的条件 第4课时 黄金分割 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
黄金分割
北师版九年级上册
新课导入
A
B
C
L
K
D
E
G
H
F
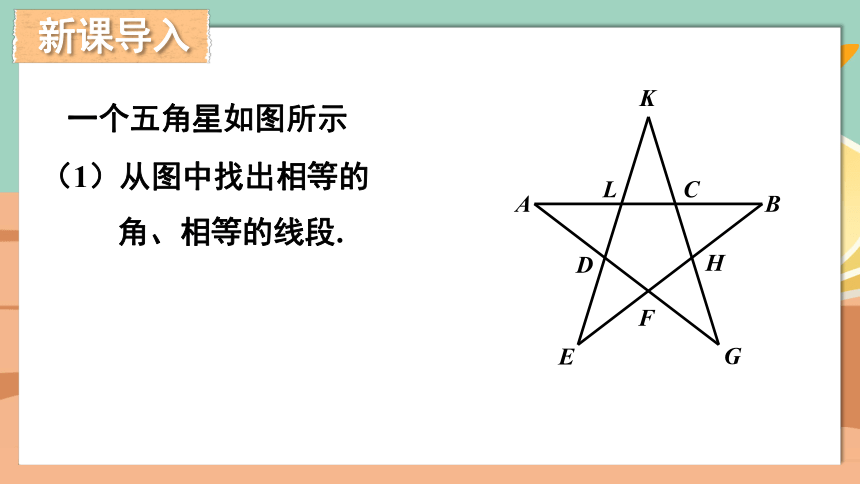
一个五角星如图所示
(1)从图中找出相等的角、相等的线段.
新课导入
A
B
C
L
K
D
E
G
H
F
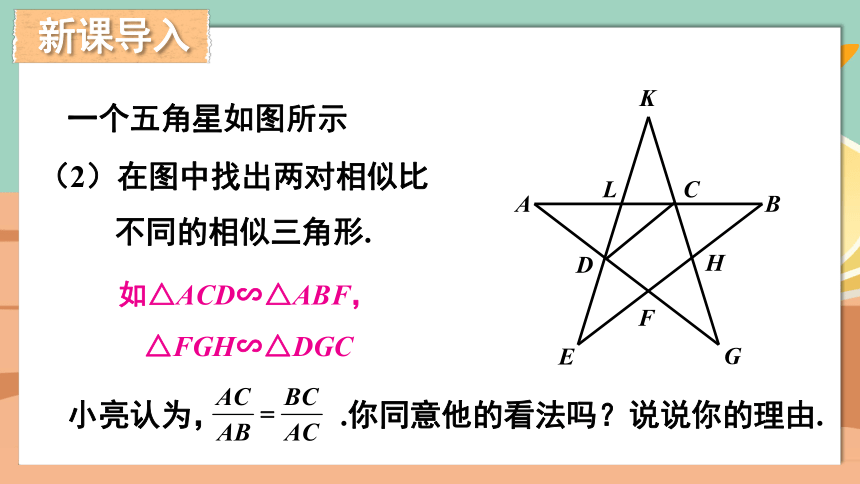
一个五角星如图所示
(2)在图中找出两对相似比不同的相似三角形.
如△ACD∽△ABF,△FGH∽△DGC
小亮认为, .你同意他的看法吗?说说你的理由.
探究新知
一般地,点C把线段AB分成两条线段AC和BC(如图),如果 ,那么线段AB被点C黄金分割,点C叫做线段的黄金分割点,AC与AB的比叫黄金比.
A
B
C
A
A
C
例 计算黄金比.
解:由 ,得AC 2=AB·BC
设AB=1,AC=x,
∴ x2=1×(1-x)
即x2+x-1=0
解这个方程,得
(不合题意,舍去)
则BC=1-x .
所以,黄金比
较长线段
原线段
=
较短线段
较长线段
比值称为黄金比,近似值为0.618
线段AB被点C黄金分割
黄金分割点
归纳总结
A
A
C
黄金比是一个比值﹐它没有单位!
A
B
C
黄金分割是一种分割线段的方法,每条线段有两个黄金分割点.如图,点C和点D都是线段AB的黄金分割点.
D
并且AD=BC,AC=BD.
古希腊时期的巴台农神庙
想一想
A
B
D
C
E
F
图1
图2
如果把图1中用虚线表示的矩形画成图2中的 ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD.
想一想
A
B
D
C
E
F
图1
图2
那么我们可以惊奇地发现 点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗
想一想
A
B
D
C
E
F
图2
由
,可得
即
因此点E是AB的黄金分割点.
是黄金比,
(即 )
也就是说,矩形ABCD的宽与长的比是黄金比.
黄金分割在几何作图上有很多应用,如五角星形的各边是按黄金分割划分的.
A
B
C
L
K
D
E
G
H
F
黄金分割也被应用于各种艺术品创作当中
绘画:《蒙娜丽莎》
雕像:《维纳斯》
苹果logo
影视中的黄金分割使画面更加自然大方与舒适
公认最完美的人体比例也和黄金分割挂钩
自然界中的黄金分割
生活中的黄金分割
拓 展
黄金分割点的作法:
方法一:
如图,已知线段AB,
(1)过点B作BD⊥AB,使AB=2BD;
(2)连接AD,在DA上截取DE=DB;
(3)在AB上截取AC=AE;
点C即为所求的黄金分割点.
A
B
D
E
C
拓 展
黄金分割点的作法:
方法二:
如图,已知线段AB,
(1)以线段AB为边作正方形ABCD;
(2)取AD的中点E,连接EB;
(3)延长DA至点F,使EF=EB;
(4)以AF为边作正方形AFGH;
A
B
D
C
E
点H即为所求的黄金分割点.
F
G
H
课堂小结
较长线段
原线段
=
较短线段
较长线段
比值称为黄金比,近似值为0.618
线段AB被点C黄金分割
黄金分割点
A
A
C
课后作业
1. 从课后习题中选取;
2. 完成练习册本课时的习题.
黄金分割
北师版九年级上册
新课导入
A
B
C
L
K
D
E
G
H
F
一个五角星如图所示
(1)从图中找出相等的角、相等的线段.
新课导入
A
B
C
L
K
D
E
G
H
F
一个五角星如图所示
(2)在图中找出两对相似比不同的相似三角形.
如△ACD∽△ABF,△FGH∽△DGC
小亮认为, .你同意他的看法吗?说说你的理由.
探究新知
一般地,点C把线段AB分成两条线段AC和BC(如图),如果 ,那么线段AB被点C黄金分割,点C叫做线段的黄金分割点,AC与AB的比叫黄金比.
A
B
C
A
A
C
例 计算黄金比.
解:由 ,得AC 2=AB·BC
设AB=1,AC=x,
∴ x2=1×(1-x)
即x2+x-1=0
解这个方程,得
(不合题意,舍去)
则BC=1-x .
所以,黄金比
较长线段
原线段
=
较短线段
较长线段
比值称为黄金比,近似值为0.618
线段AB被点C黄金分割
黄金分割点
归纳总结
A
A
C
黄金比是一个比值﹐它没有单位!
A
B
C
黄金分割是一种分割线段的方法,每条线段有两个黄金分割点.如图,点C和点D都是线段AB的黄金分割点.
D
并且AD=BC,AC=BD.
古希腊时期的巴台农神庙
想一想
A
B
D
C
E
F
图1
图2
如果把图1中用虚线表示的矩形画成图2中的 ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD.
想一想
A
B
D
C
E
F
图1
图2
那么我们可以惊奇地发现 点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗
想一想
A
B
D
C
E
F
图2
由
,可得
即
因此点E是AB的黄金分割点.
是黄金比,
(即 )
也就是说,矩形ABCD的宽与长的比是黄金比.
黄金分割在几何作图上有很多应用,如五角星形的各边是按黄金分割划分的.
A
B
C
L
K
D
E
G
H
F
黄金分割也被应用于各种艺术品创作当中
绘画:《蒙娜丽莎》
雕像:《维纳斯》
苹果logo
影视中的黄金分割使画面更加自然大方与舒适
公认最完美的人体比例也和黄金分割挂钩
自然界中的黄金分割
生活中的黄金分割
拓 展
黄金分割点的作法:
方法一:
如图,已知线段AB,
(1)过点B作BD⊥AB,使AB=2BD;
(2)连接AD,在DA上截取DE=DB;
(3)在AB上截取AC=AE;
点C即为所求的黄金分割点.
A
B
D
E
C
拓 展
黄金分割点的作法:
方法二:
如图,已知线段AB,
(1)以线段AB为边作正方形ABCD;
(2)取AD的中点E,连接EB;
(3)延长DA至点F,使EF=EB;
(4)以AF为边作正方形AFGH;
A
B
D
C
E
点H即为所求的黄金分割点.
F
G
H
课堂小结
较长线段
原线段
=
较短线段
较长线段
比值称为黄金比,近似值为0.618
线段AB被点C黄金分割
黄金分割点
A
A
C
课后作业
1. 从课后习题中选取;
2. 完成练习册本课时的习题.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
