【高效备课】北师大版九(上) 第4章 图形的相似 回顾与思考 课件
文档属性
| 名称 | 【高效备课】北师大版九(上) 第4章 图形的相似 回顾与思考 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 11:35:06 | ||
图片预览









文档简介
(共32张PPT)
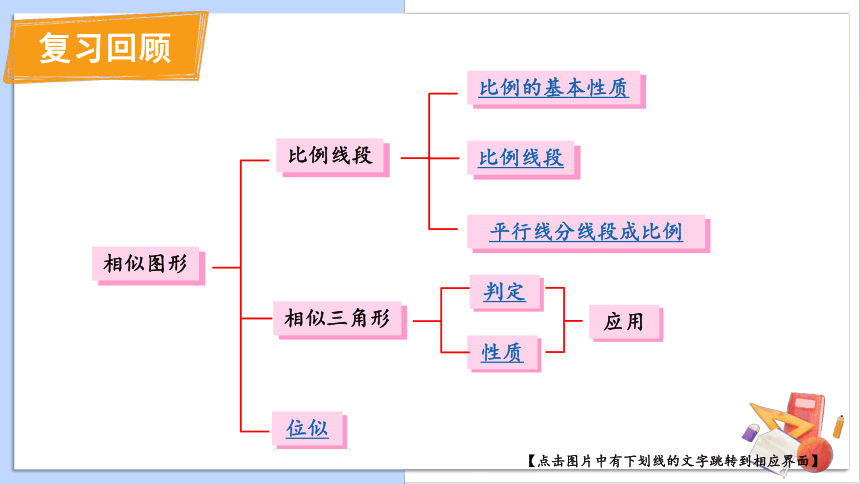
回顾与思考
4
北师版九年级上册
相似图形
比例线段
相似三角形
位似
比例的基本性质
比例线段
平行线分线段成比例
判定
性质
应用
【点击图片中有下划线的文字跳转到相应界面】
复习回顾
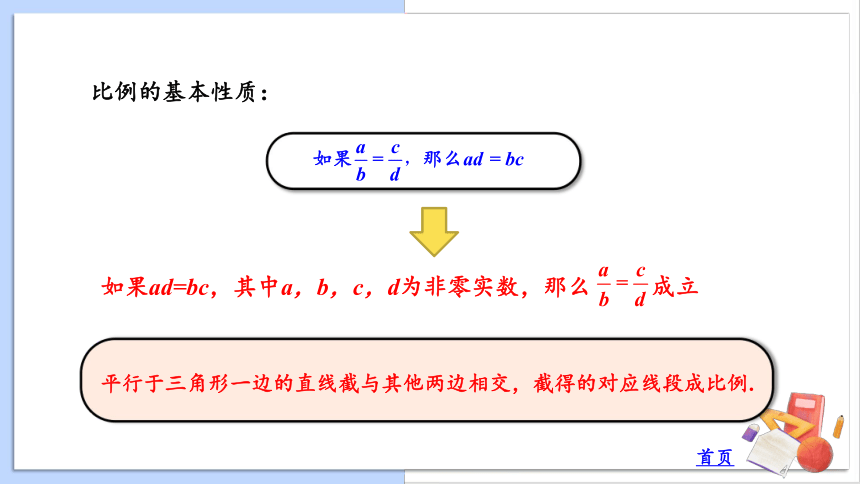
比例的基本性质:
如果ad=bc,其中a,b,c,d为非零实数,那么 成立
平行于三角形一边的直线截与其他两边相交,截得的对应线段成比例.
首页
两角分别相等的两个三角形相似
相似三角形判定定理1
两边成比例且夹角相等的两个三角形相似
相似三角形判定定理2
三边成比例的两个三角形相似.
相似三角形判定定理3
首页
相似三角形对应高的比、对应的角平分线的比、对应边上的中线的比等于相似比.
相似三角形的性质
相似三角形的周长的比等于相似比,面积比等于相似比的平方.
首页
在平面直角坐标系中,将一个多边形每个顶点的横坐标,纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为 .
位似
首页
1.判断正误:
(1)若线段a=5cm, b=2cm,则a : b=5 : 2; ( )
(2)若A,B两地在地图上的距离为7cm,地图的比例尺为l∶5000,则A,B两地的实际距离为35m; ( )
(3)若线段AB= cm,C是AB的黄金分割点,且AC > BC,则 cm. ( )
√
×
√
随堂练习
2. (1)四条线段a, b,c,d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长.
(2)已知 ,且a+b-2c =3,求a的值.
6a=3×2,∴a=1cm
代入a+b-2c =3中,求得a=6
3.如图,已知直线a//b//c,分别交直线 m,n于点A,C,E,B,D,F,AC=4,CE=6,BD=3,求BF的长.
m
n
a
b
c
A
C
E
B
D
F
∵ AC=4,CE=6,BD=3
∴解得 DF=4.5
∴BF=4.5+3=7.5
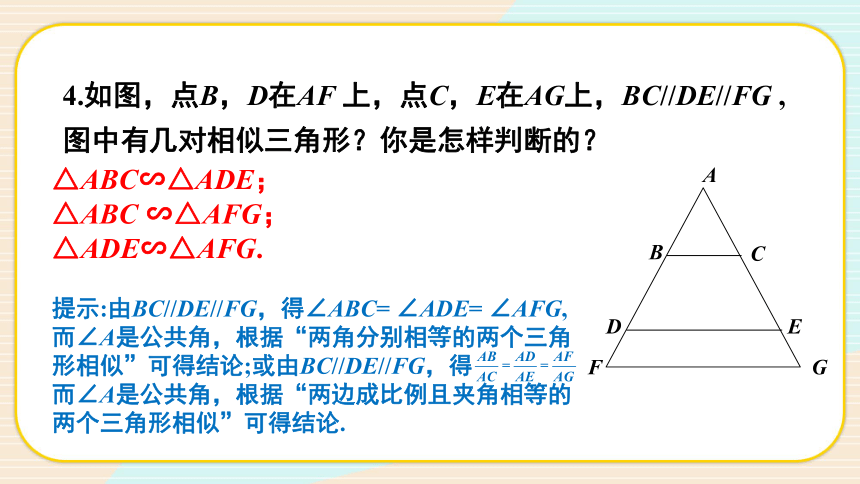
4.如图,点B,D在AF 上,点C,E在AG上,BC//DE//FG ,图中有几对相似三角形?你是怎样判断的?
A
C
E
B
D
F
G
△ABC∽△ADE;
△ABC ∽△AFG;
△ADE∽△AFG.
提示:由BC//DE//FG,得∠ABC= ∠ADE= ∠AFG,而∠A是公共角,根据“两角分别相等的两个三角形相似”可得结论;或由BC//DE//FG,得 而∠A是公共角,根据“两边成比例且夹角相等的两个三角形相似”可得结论.
5.如图,点D,E分别是AB和AC上的点,△ADE∽△ABC,AD=2acm,DB=acm,BC=bcm,∠A=70°, ∠B=50°.
A
C
E
B
D
(1)求∠ADE的度数;(2)求∠AED的度数;(3)求DE 的长.
解 (1)∠B=∠ADE=50°
(2)∠AED=∠C=180°-∠A -∠B
=180°-70°-50°=60°
∵ BC=bcm
6.如果两个相似三角形面积比为4∶9,那么这两个相似三角形对应边的比是多少?
这两个相似三角形对应边的比是2∶3
7.如图,在△ABC中,点D,E分别是AB和AC上的点,DE∥BC、AD=3BD,S△ABC=48,求S△ADE.
A
C
E
B
D
解 ∵DE∥BC
∴△ABC∽△ADE
∵AD=3BD
∴AD= AB
∵ S△ABC=48
∴ S△ADE=27
8.如图,AB与CD相交于点O,且AC∥BD.OA·OD=OC·OB成立吗?为什么?
A
C
O
B
D
证明 成立.
∵ AC∥BD
∴∠D=∠C, ∠B=∠A
∴△DOB∽△AOC
∴OA·OD=OC·OB
9.如图,在△ABC中,D,E分别是AB和AC上的点,且AD=31,DB=29,AE=30,EC=32.请找出∠1,∠2,∠3,∠4中相等的角.
证明 ∵ AD=31,DB=29,AE=30,EC=32
∴AB=60,AC=62
∴△ABC∽△AED
∴∠1=∠4,∠2=∠3
10. 公园中的儿童游乐场是两个相似三角形地块,相似比为2∶3,面积的差为30m2,它们的面积之和为多少
11.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
A
C
B
D
P
解 ∵△ACP∽△PDB
∴∠A=∠BPD,∠B=∠APC
∵∠CPD+2∠BPD+2∠APC=180°
且∠CPD=60°
∴2∠BPD+2∠APC=120°
∴∠BPD+∠APC=60°
∴ ∠APB=∠BPD+∠APC+∠CPD =120°
12.如图,在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A (6,0), B (6,4),C(0,4).已知矩形OA'B'C'与矩形OABC位似,位似中心是原点O,且矩形OA'B'C'的面积等于矩形OABC面积的 ,求点B'的坐标.
∴两个四边形的相似比是
∴ B′(3,2)
13.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,在DC的延长线上去一点E,连接OE交BC于点F.已知AB=a,BC=b,CE=c,求CF的长.
A
C
B
D
G
F
E
O
解 如图,延长EO与AD相交于点G
∵OA=OC,∠OAG=∠OCF, ∠AOG=∠COF
∴△AOG≌△COF
∴AG=CF
∵BC∥AD,
∴△CEF∽△DEG
∵ AB=a,BC=b,CE=c
解得 CF=
14.如图,在平面直角坐标系中,将四边形OABC四个顶点的横坐标、纵坐标分别乘-2,画出以所得四个点为顶点的四边形,并指出这两个四边形的位似中心和相似比.
O
x
y
2
4
6
2
4
6
-2
-4
8
-2
-4
-6
-8
-10
A
B
C
A′(-4,-8)
B′(4,-10)
C′(8,0)
15.将三角形各边向外平移1个单位并适当延长,得到如图
(1)所示的图形,变化前后的两个三角形相似吗?如果把三角形改为正方形、长方形呢?(如图(2)(3))
三角形和正方形相似,长方形不相似
16.如图,BC与EF在一条直线上,AC∥DF.将图(2)的三角形截去一块,使它变为与图(1)相似的图形.
沿着直线l截去上面一块,就可以变为与图(1)相似的图形
17.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q、求BP : PQ: QR.
BP∶PQ∶QR =3∶1∶2.
提示:易证BC=CE,PC//RE,于是BP=PR,
,△PCQ∽△RDQ,所以
, 所以 , .
18.如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= .BC=1,BF分别交AC,DC,DE于点P,Q,R.
(1)求证:△BFG∽△FEG;(2)求AP : PC.
且可知 ∠BGF=∠FGE
∴ △BFG∽△FEG
18.如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= .BC=1,BF分别交AC,DC,DE于点P,Q,R.
(1)求证:△BFG∽△FEG;(2)求AP : PC.
(2)由(1)可知∠PBC=∠EFG=∠BAC,
又∠BCP=∠ACB
∴△BCP∽△ACB
∴AP∶PC=2∶1
19.如图,在平面直角坐标系中,以原点О为位似中心画一个四边形,使它与矩形OBCD位似,且相似比为1∶2.你有几种方法?
O
x
y
2
4
6
2
4
6
-2
-4
8
-2
-4
-6
-8
-10
D
B
C
D′(0,2)
B′(4,0)
C′(4,2)
D′′(0,-2)
B′′(-4,0)
C′′(-4,-2)
20.如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知 AB= 10m,CD=15m,求点M离地面的高度MH.
解 ∵AB∥CD,∴△ABM∽△CDM
BH等于△ABM的边AB上的高,
HD等于△CDM的边CD上的高.
∵MH∥CD,∴△BHM∽△BDC,
21.一块直角三角形木板的面积为1.5m2,一条直角边AB为 1.5m,怎样才能把它加第四章图形的相似工成一个无拼接的面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你用学过的知识说明哪位木匠的方法符合要求(加工损耗忽略不计,计算结果中的分数可保留).
解 由题意可知BC=2m,AC=2.5m
在图(甲)中,过点B作AC的垂线,分别交ED和AC于点K,H,求得BH=1.2m.设正方形的边长为xm,∵△BDE∽△BCA
在图(乙)中,设正方形的边长为ym,∵△BDE∽△BCA
因为y>x,所以乙的面积更大.
K
H
22.如图,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=14,点P在BD上移动,当以P、C、D为顶点的三角形与△ABP相似时,求PB的长.
两个三角形相似有两种情况:
(1)∠A=∠CPD.此时有 ,即 ,
求得PB=12或2.
(2)∠A=∠C.此时有 ,即 ,
求得PB=8.4.
23.如图,△ABC的三边长分别为a, b,c ( a>b > c ),△A1B1C1的三边长分别为a1,b1,c1, △ABC∽△A1B1C1 ,相似比为k (k>-1) .
(1)若c=a1,求证:a = kc;
(2)若c =a1,试给出符合条件的一对△ABC和△A1B1C1 ,使得a,b,c和a1,b1,c1都是正整数;
(3)若b=a,c=b1,是否存在△ABC和△ABC使得k=2?请说明理由.
(2)答案不唯一,如可以取a=8,b=6,c=4,
a1=4,b1=3,c1=2,
所以△ABC∽△A1B1C1
(3)不存在这样的△ABC和△A1B1C1.
若k=2,则a=2a1, b=2b1, c=2c1;
于是a=2a1=2b=4b1=4c,所以b=2c;所以b+c=2c+c<4c=a,这与b+c>a相矛盾.
回顾与思考
4
北师版九年级上册
相似图形
比例线段
相似三角形
位似
比例的基本性质
比例线段
平行线分线段成比例
判定
性质
应用
【点击图片中有下划线的文字跳转到相应界面】
复习回顾
比例的基本性质:
如果ad=bc,其中a,b,c,d为非零实数,那么 成立
平行于三角形一边的直线截与其他两边相交,截得的对应线段成比例.
首页
两角分别相等的两个三角形相似
相似三角形判定定理1
两边成比例且夹角相等的两个三角形相似
相似三角形判定定理2
三边成比例的两个三角形相似.
相似三角形判定定理3
首页
相似三角形对应高的比、对应的角平分线的比、对应边上的中线的比等于相似比.
相似三角形的性质
相似三角形的周长的比等于相似比,面积比等于相似比的平方.
首页
在平面直角坐标系中,将一个多边形每个顶点的横坐标,纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比为 .
位似
首页
1.判断正误:
(1)若线段a=5cm, b=2cm,则a : b=5 : 2; ( )
(2)若A,B两地在地图上的距离为7cm,地图的比例尺为l∶5000,则A,B两地的实际距离为35m; ( )
(3)若线段AB= cm,C是AB的黄金分割点,且AC > BC,则 cm. ( )
√
×
√
随堂练习
2. (1)四条线段a, b,c,d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长.
(2)已知 ,且a+b-2c =3,求a的值.
6a=3×2,∴a=1cm
代入a+b-2c =3中,求得a=6
3.如图,已知直线a//b//c,分别交直线 m,n于点A,C,E,B,D,F,AC=4,CE=6,BD=3,求BF的长.
m
n
a
b
c
A
C
E
B
D
F
∵ AC=4,CE=6,BD=3
∴解得 DF=4.5
∴BF=4.5+3=7.5
4.如图,点B,D在AF 上,点C,E在AG上,BC//DE//FG ,图中有几对相似三角形?你是怎样判断的?
A
C
E
B
D
F
G
△ABC∽△ADE;
△ABC ∽△AFG;
△ADE∽△AFG.
提示:由BC//DE//FG,得∠ABC= ∠ADE= ∠AFG,而∠A是公共角,根据“两角分别相等的两个三角形相似”可得结论;或由BC//DE//FG,得 而∠A是公共角,根据“两边成比例且夹角相等的两个三角形相似”可得结论.
5.如图,点D,E分别是AB和AC上的点,△ADE∽△ABC,AD=2acm,DB=acm,BC=bcm,∠A=70°, ∠B=50°.
A
C
E
B
D
(1)求∠ADE的度数;(2)求∠AED的度数;(3)求DE 的长.
解 (1)∠B=∠ADE=50°
(2)∠AED=∠C=180°-∠A -∠B
=180°-70°-50°=60°
∵ BC=bcm
6.如果两个相似三角形面积比为4∶9,那么这两个相似三角形对应边的比是多少?
这两个相似三角形对应边的比是2∶3
7.如图,在△ABC中,点D,E分别是AB和AC上的点,DE∥BC、AD=3BD,S△ABC=48,求S△ADE.
A
C
E
B
D
解 ∵DE∥BC
∴△ABC∽△ADE
∵AD=3BD
∴AD= AB
∵ S△ABC=48
∴ S△ADE=27
8.如图,AB与CD相交于点O,且AC∥BD.OA·OD=OC·OB成立吗?为什么?
A
C
O
B
D
证明 成立.
∵ AC∥BD
∴∠D=∠C, ∠B=∠A
∴△DOB∽△AOC
∴OA·OD=OC·OB
9.如图,在△ABC中,D,E分别是AB和AC上的点,且AD=31,DB=29,AE=30,EC=32.请找出∠1,∠2,∠3,∠4中相等的角.
证明 ∵ AD=31,DB=29,AE=30,EC=32
∴AB=60,AC=62
∴△ABC∽△AED
∴∠1=∠4,∠2=∠3
10. 公园中的儿童游乐场是两个相似三角形地块,相似比为2∶3,面积的差为30m2,它们的面积之和为多少
11.如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
A
C
B
D
P
解 ∵△ACP∽△PDB
∴∠A=∠BPD,∠B=∠APC
∵∠CPD+2∠BPD+2∠APC=180°
且∠CPD=60°
∴2∠BPD+2∠APC=120°
∴∠BPD+∠APC=60°
∴ ∠APB=∠BPD+∠APC+∠CPD =120°
12.如图,在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A (6,0), B (6,4),C(0,4).已知矩形OA'B'C'与矩形OABC位似,位似中心是原点O,且矩形OA'B'C'的面积等于矩形OABC面积的 ,求点B'的坐标.
∴两个四边形的相似比是
∴ B′(3,2)
13.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,在DC的延长线上去一点E,连接OE交BC于点F.已知AB=a,BC=b,CE=c,求CF的长.
A
C
B
D
G
F
E
O
解 如图,延长EO与AD相交于点G
∵OA=OC,∠OAG=∠OCF, ∠AOG=∠COF
∴△AOG≌△COF
∴AG=CF
∵BC∥AD,
∴△CEF∽△DEG
∵ AB=a,BC=b,CE=c
解得 CF=
14.如图,在平面直角坐标系中,将四边形OABC四个顶点的横坐标、纵坐标分别乘-2,画出以所得四个点为顶点的四边形,并指出这两个四边形的位似中心和相似比.
O
x
y
2
4
6
2
4
6
-2
-4
8
-2
-4
-6
-8
-10
A
B
C
A′(-4,-8)
B′(4,-10)
C′(8,0)
15.将三角形各边向外平移1个单位并适当延长,得到如图
(1)所示的图形,变化前后的两个三角形相似吗?如果把三角形改为正方形、长方形呢?(如图(2)(3))
三角形和正方形相似,长方形不相似
16.如图,BC与EF在一条直线上,AC∥DF.将图(2)的三角形截去一块,使它变为与图(1)相似的图形.
沿着直线l截去上面一块,就可以变为与图(1)相似的图形
17.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q、求BP : PQ: QR.
BP∶PQ∶QR =3∶1∶2.
提示:易证BC=CE,PC//RE,于是BP=PR,
,△PCQ∽△RDQ,所以
, 所以 , .
18.如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= .BC=1,BF分别交AC,DC,DE于点P,Q,R.
(1)求证:△BFG∽△FEG;(2)求AP : PC.
且可知 ∠BGF=∠FGE
∴ △BFG∽△FEG
18.如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB= .BC=1,BF分别交AC,DC,DE于点P,Q,R.
(1)求证:△BFG∽△FEG;(2)求AP : PC.
(2)由(1)可知∠PBC=∠EFG=∠BAC,
又∠BCP=∠ACB
∴△BCP∽△ACB
∴AP∶PC=2∶1
19.如图,在平面直角坐标系中,以原点О为位似中心画一个四边形,使它与矩形OBCD位似,且相似比为1∶2.你有几种方法?
O
x
y
2
4
6
2
4
6
-2
-4
8
-2
-4
-6
-8
-10
D
B
C
D′(0,2)
B′(4,0)
C′(4,2)
D′′(0,-2)
B′′(-4,0)
C′′(-4,-2)
20.如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知 AB= 10m,CD=15m,求点M离地面的高度MH.
解 ∵AB∥CD,∴△ABM∽△CDM
BH等于△ABM的边AB上的高,
HD等于△CDM的边CD上的高.
∵MH∥CD,∴△BHM∽△BDC,
21.一块直角三角形木板的面积为1.5m2,一条直角边AB为 1.5m,怎样才能把它加第四章图形的相似工成一个无拼接的面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你用学过的知识说明哪位木匠的方法符合要求(加工损耗忽略不计,计算结果中的分数可保留).
解 由题意可知BC=2m,AC=2.5m
在图(甲)中,过点B作AC的垂线,分别交ED和AC于点K,H,求得BH=1.2m.设正方形的边长为xm,∵△BDE∽△BCA
在图(乙)中,设正方形的边长为ym,∵△BDE∽△BCA
因为y>x,所以乙的面积更大.
K
H
22.如图,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=14,点P在BD上移动,当以P、C、D为顶点的三角形与△ABP相似时,求PB的长.
两个三角形相似有两种情况:
(1)∠A=∠CPD.此时有 ,即 ,
求得PB=12或2.
(2)∠A=∠C.此时有 ,即 ,
求得PB=8.4.
23.如图,△ABC的三边长分别为a, b,c ( a>b > c ),△A1B1C1的三边长分别为a1,b1,c1, △ABC∽△A1B1C1 ,相似比为k (k>-1) .
(1)若c=a1,求证:a = kc;
(2)若c =a1,试给出符合条件的一对△ABC和△A1B1C1 ,使得a,b,c和a1,b1,c1都是正整数;
(3)若b=a,c=b1,是否存在△ABC和△ABC使得k=2?请说明理由.
(2)答案不唯一,如可以取a=8,b=6,c=4,
a1=4,b1=3,c1=2,
所以△ABC∽△A1B1C1
(3)不存在这样的△ABC和△A1B1C1.
若k=2,则a=2a1, b=2b1, c=2c1;
于是a=2a1=2b=4b1=4c,所以b=2c;所以b+c=2c+c<4c=a,这与b+c>a相矛盾.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
