1.3探索三角形全等的条件 同步练习提高练习(无答案)苏科版数学八年级上册
文档属性
| 名称 | 1.3探索三角形全等的条件 同步练习提高练习(无答案)苏科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 284.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 20:17:41 | ||
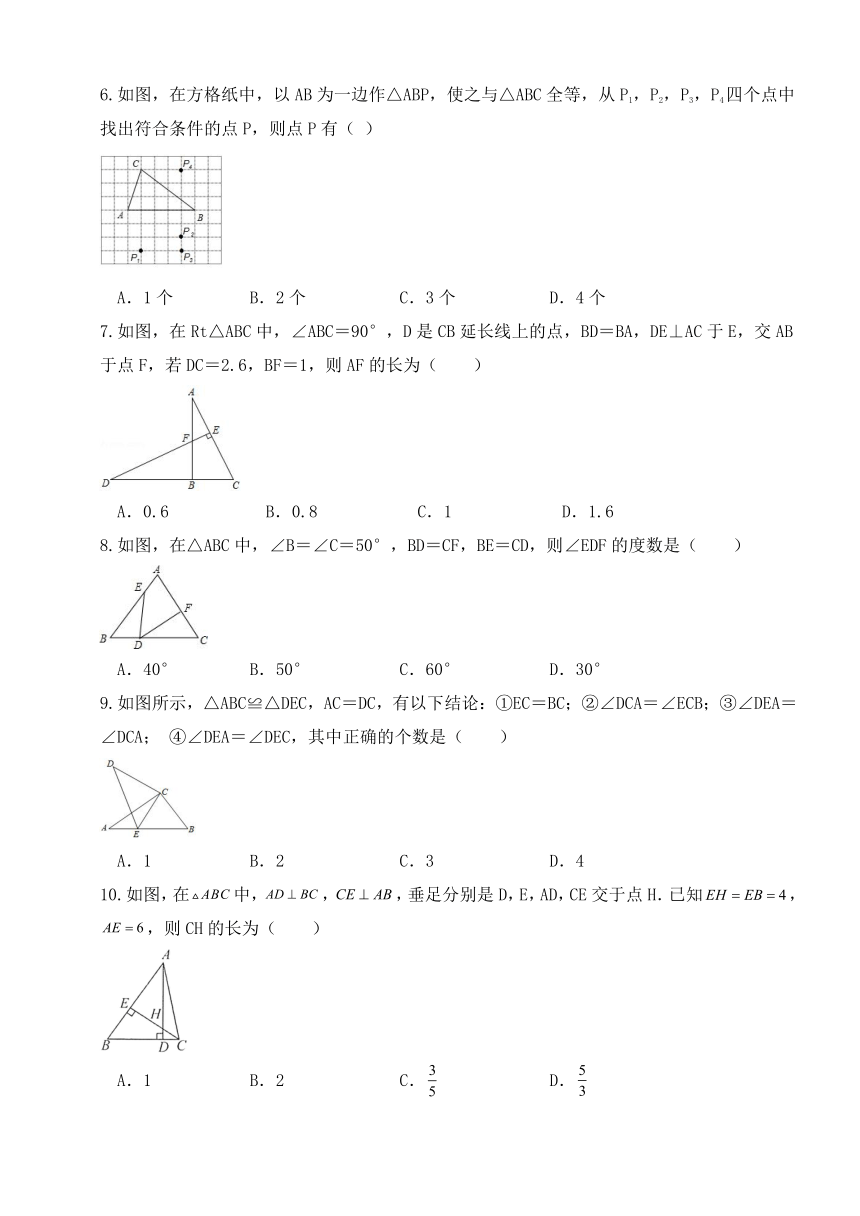
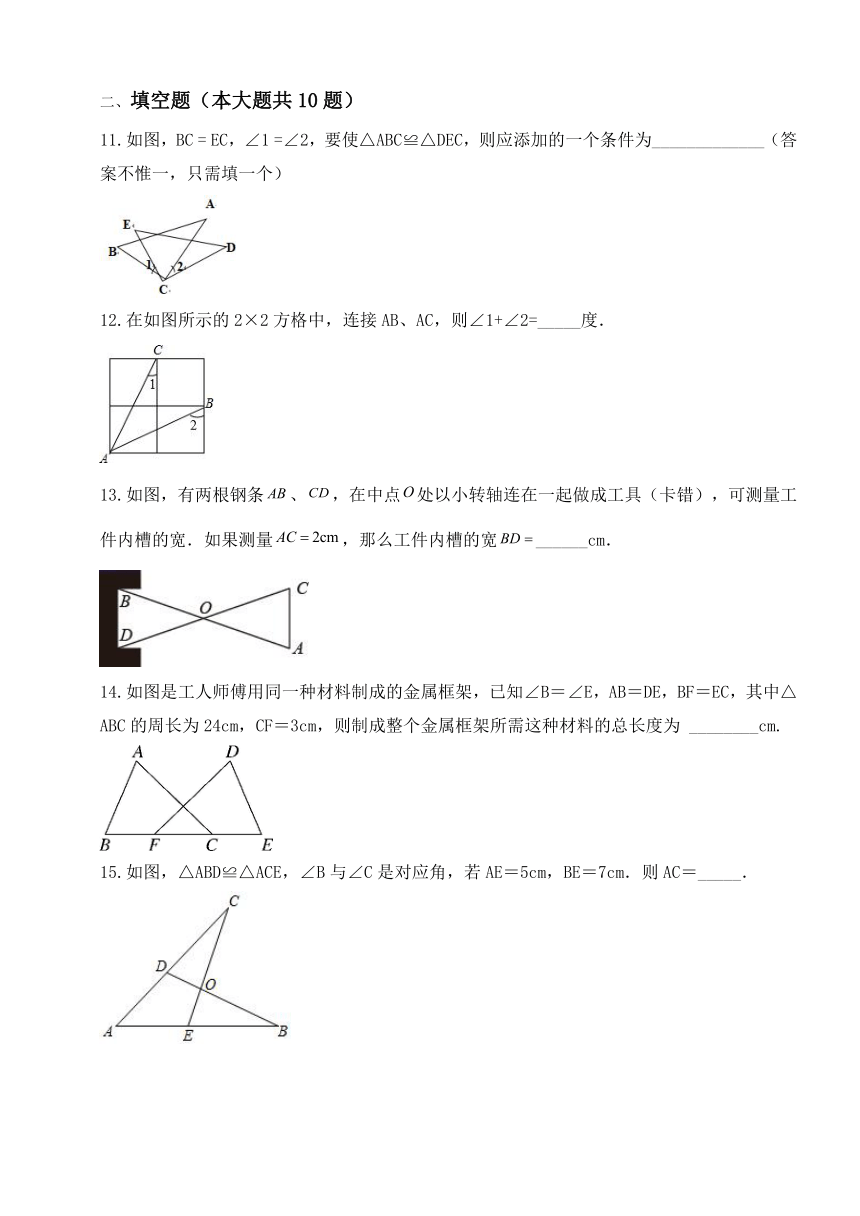
图片预览

文档简介
1.3探索三角形全等的条件 (同步练习提高)
选择题(本大题共10题)
1.如图,AC、BD相交于O,∠1=∠2,若用“SAS”说明,则还需加上条件( )
A.AD=BC B.∠D=∠C C.OA=AB D.BD=AC
2.下列两个三角形全等的是( )
A. ①② B.②③ C.③④ D.①④
3.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①去和带②去
4.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
5.如图所示,亮亮课本上的一个三角形被墨迹污染了一部分,很快他就根据所学知识画一出一个与这个三角形全等的图形,那么这两个三角形全等的依据是( )
A.SSS B.SAS C.AAS D.ASA
6.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6 B.0.8 C.1 D.1.6
8.如图,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是( )
A.40° B.50° C.60° D.30°
9.如图所示,△ABC≌△DEC,AC=DC,有以下结论:①EC=BC;②∠DCA=∠ECB;③∠DEA=∠DCA; ④∠DEA=∠DEC,其中正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为( )
A.1 B.2 C. D.
填空题(本大题共10题)
11.如图,BC = EC,∠1 =∠2,要使△ABC≌△DEC,则应添加的一个条件为_____________(答案不惟一,只需填一个)
12.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2=_____度.
13.如图,有两根钢条、,在中点处以小转轴连在一起做成工具(卡错),可测量工件内槽的宽.如果测量,那么工件内槽的宽______cm.
14.如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.
15.如图,△ABD≌△ACE,∠B与∠C是对应角,若AE=5cm,BE=7cm.则AC=_____.
16.如图,△ABC≌△ADE,则AB =______,若∠BAE=120°,∠BAD=40°,则∠BAC=______.
17.如图,点D是△ABC的边AB上一点,FC∥AB,连接DF交AC于点E,若CE=AE,AB=7,CF=4,则BD的长是 .
18.如图,在△ABC中,∠B=∠C=∠1,BD=CF=3,BE=2,则BC=______.
19.如图,,垂足分别为,若,则的长为________________________.
20.如图,若AB⊥BC于点B,AE⊥DE于点E,AB=AE,∠ACB=∠ADE,∠ACD=∠ADC=70°,∠BAD=60°,则∠BAE的度数是 .
解答题(本大题共7题)
21.如图,已知:点B、E、F、C在同一直线上,,,且求证:
22.如图,,,点、在上,且.
(1)填空:把下面的推理过程补充完整,并在括号内注明理由.
试说明:.
解:,
( ).
,
即.
( ).
又,
( ).
(2)由(1) 可得,与平行吗?请说明理由,
23.如图,已知:点在同一条直线上,AD∥CB,,.
(1)判断线段与的数量关系,并说明理由;
(2)判断线段与的位置关系,并说明理由.
24.如图,在Rt△ABC中,∠ABC=90°点D在BC的延长线上,且BD=AB.过点B作BE⊥AC,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
25.如图,已知AB=AC,E,D分别是AB,AC的中点,且AF⊥BD交BD的延长线于F,AG⊥CE交CE的延长线于G,试判断AF和AG的关系是否相等,并说明理由.
26.如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上.
(1)求证:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长.
27.直线,与的平分线交于点C,过点C作一条直线分别与直线PA,QB相交于点D,E.
(1)如图(1),当直线l与PA垂直时,求证:.
(2)如图(2),当直线l与PA不垂直且点D,E在AB同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.
(3)当直线l与PA不垂直且点D,E在AB异侧时,(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,请写出AD,BE,AB之间的数量关系(不用证明).
选择题(本大题共10题)
1.如图,AC、BD相交于O,∠1=∠2,若用“SAS”说明,则还需加上条件( )
A.AD=BC B.∠D=∠C C.OA=AB D.BD=AC
2.下列两个三角形全等的是( )
A. ①② B.②③ C.③④ D.①④
3.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①去和带②去
4.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有( )
A.1对 B.2对 C.3对 D.4对
5.如图所示,亮亮课本上的一个三角形被墨迹污染了一部分,很快他就根据所学知识画一出一个与这个三角形全等的图形,那么这两个三角形全等的依据是( )
A.SSS B.SAS C.AAS D.ASA
6.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6 B.0.8 C.1 D.1.6
8.如图,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是( )
A.40° B.50° C.60° D.30°
9.如图所示,△ABC≌△DEC,AC=DC,有以下结论:①EC=BC;②∠DCA=∠ECB;③∠DEA=∠DCA; ④∠DEA=∠DEC,其中正确的个数是( )
A.1 B.2 C.3 D.4
10.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为( )
A.1 B.2 C. D.
填空题(本大题共10题)
11.如图,BC = EC,∠1 =∠2,要使△ABC≌△DEC,则应添加的一个条件为_____________(答案不惟一,只需填一个)
12.在如图所示的2×2方格中,连接AB、AC,则∠1+∠2=_____度.
13.如图,有两根钢条、,在中点处以小转轴连在一起做成工具(卡错),可测量工件内槽的宽.如果测量,那么工件内槽的宽______cm.
14.如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.
15.如图,△ABD≌△ACE,∠B与∠C是对应角,若AE=5cm,BE=7cm.则AC=_____.
16.如图,△ABC≌△ADE,则AB =______,若∠BAE=120°,∠BAD=40°,则∠BAC=______.
17.如图,点D是△ABC的边AB上一点,FC∥AB,连接DF交AC于点E,若CE=AE,AB=7,CF=4,则BD的长是 .
18.如图,在△ABC中,∠B=∠C=∠1,BD=CF=3,BE=2,则BC=______.
19.如图,,垂足分别为,若,则的长为________________________.
20.如图,若AB⊥BC于点B,AE⊥DE于点E,AB=AE,∠ACB=∠ADE,∠ACD=∠ADC=70°,∠BAD=60°,则∠BAE的度数是 .
解答题(本大题共7题)
21.如图,已知:点B、E、F、C在同一直线上,,,且求证:
22.如图,,,点、在上,且.
(1)填空:把下面的推理过程补充完整,并在括号内注明理由.
试说明:.
解:,
( ).
,
即.
( ).
又,
( ).
(2)由(1) 可得,与平行吗?请说明理由,
23.如图,已知:点在同一条直线上,AD∥CB,,.
(1)判断线段与的数量关系,并说明理由;
(2)判断线段与的位置关系,并说明理由.
24.如图,在Rt△ABC中,∠ABC=90°点D在BC的延长线上,且BD=AB.过点B作BE⊥AC,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
25.如图,已知AB=AC,E,D分别是AB,AC的中点,且AF⊥BD交BD的延长线于F,AG⊥CE交CE的延长线于G,试判断AF和AG的关系是否相等,并说明理由.
26.如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上.
(1)求证:AC=AE;
(2)若AC=8,AB=10,且△ABC的面积等于24,求DE的长.
27.直线,与的平分线交于点C,过点C作一条直线分别与直线PA,QB相交于点D,E.
(1)如图(1),当直线l与PA垂直时,求证:.
(2)如图(2),当直线l与PA不垂直且点D,E在AB同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.
(3)当直线l与PA不垂直且点D,E在AB异侧时,(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,请写出AD,BE,AB之间的数量关系(不用证明).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
