2023-2024学年人教版数学八年级上册12.2三角形全等的判定 同步训练(含解析)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册12.2三角形全等的判定 同步训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 394.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 07:02:31 | ||
图片预览


文档简介
12.2三角形全等的判定
一、单选题
1.如图是用直尺和圆规作已知角∠AOB平分线OP的示意图,仔细观察,根据三角形全等的知识,说明画出OP的依据是()
A.边角边,全等三角形对应角相等
B.角边角,全等三角形对应角相等
C.边边边,全等三角形对应角相等
D.斜边直角边,全等三角形对应角相等
2.已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A.△ABC≌△XYZ B.△DEF≌△XYZ
C. D.
3.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )
A.71° B.76° C.78° D.80°
4.下列条件能够判断两个三角形全等的是( )
A.两个三角形周长相等
B.两个三角形三个内角分别相等
C.两个三角形有两条边和其中一条边上的中线分别相等
D.两个三角形有两条边和一对角分别相等
5.如图,在ABC中,AB=AC,AD⊥BC于点D,则下列结论,一定成立的是( )
A.BD=AD B.∠B=∠C
C.AD=CD D.∠BAD=∠ACD
6.如图,已知∠BAD=∠CAE,AC=AE,下列添加的条件中不能证明 是( )
A.DE=BC B.AB=AD C.∠C=∠E D.∠B=∠D
7.如图,点在上,点在上,已知,添加下列一个条件后仍无法判定的是( )
A. B. C. D.
8.如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )
A.BC+AD=CD B.E为CD中点
C.∠AEB=90° D.S△ABE=S四边形ABCD
二、填空题
9.如图,已知,请你添加一个条件,能运用直接说明≌,你添加的条件是
不添加任何字母和辅助线
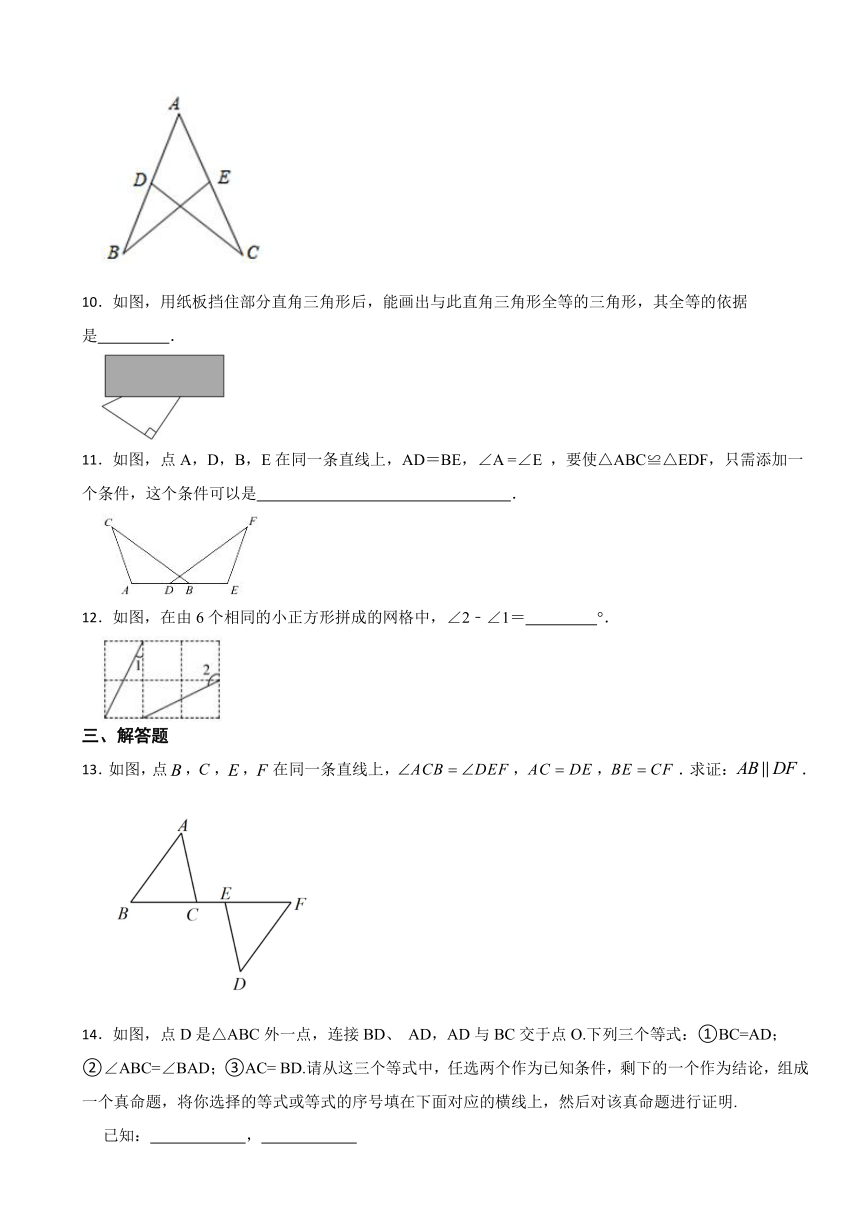
10.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是 .
11.如图,点A,D,B,E在同一条直线上,AD=BE,∠A =∠E ,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 .
12.如图,在由6个相同的小正方形拼成的网格中,∠2﹣∠1= °.
三、解答题
13.如图,点,,,在同一条直线上,,,.求证:.
14.如图,点D是△ABC外一点,连接BD、 AD,AD与BC交于点O.下列三个等式:①BC=AD;②∠ABC=∠BAD;③AC= BD.请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明.
已知: ,
求证:
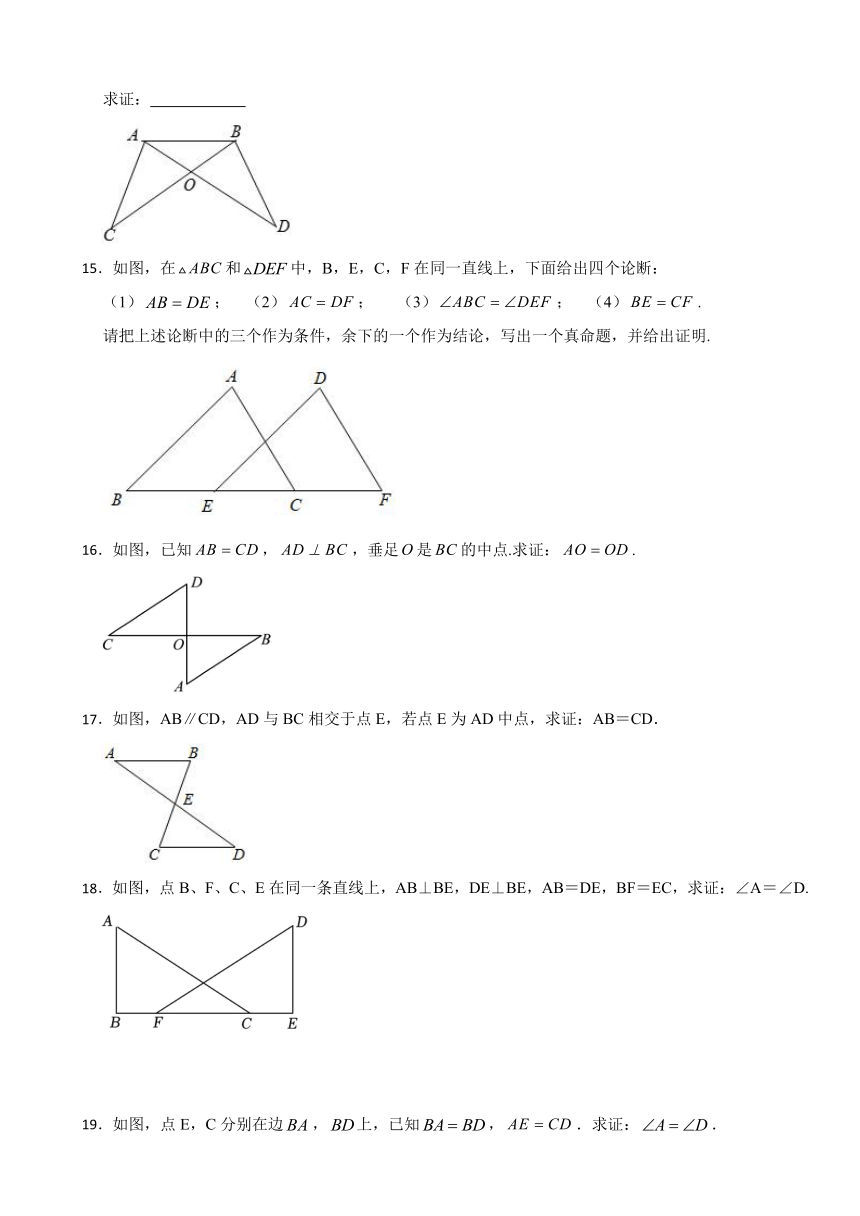
15.如图,在和中,B,E,C,F在同一直线上,下面给出四个论断:
(1); (2); (3); (4).
请把上述论断中的三个作为条件,余下的一个作为结论,写出一个真命题,并给出证明.
16.如图,已知,,垂足是的中点.求证:.
17.如图,AB∥CD,AD与BC相交于点E,若点E为AD中点,求证:AB=CD.
18.如图,点B、F、C、E在同一条直线上,AB⊥BE,DE⊥BE,AB=DE,BF=EC,求证:∠A=∠D.
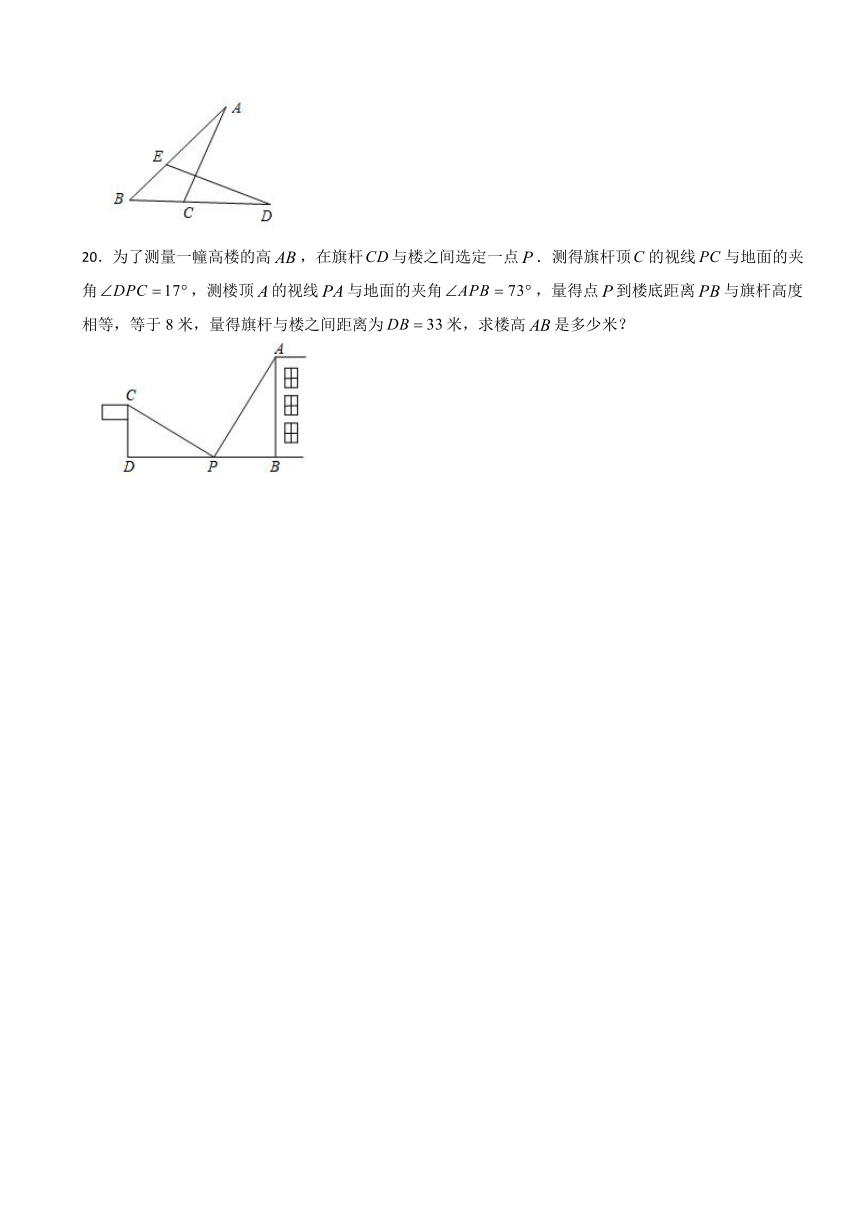
19.如图,点E,C分别在边,上,已知,.求证:.
20.为了测量一幢高楼的高,在旗杆与楼之间选定一点.测得旗杆顶的视线与地面的夹角,测楼顶的视线与地面的夹角,量得点到楼底距离与旗杆高度相等,等于8米,量得旗杆与楼之间距离为米,求楼高是多少米?
答案解析部分
1.【答案】C
【解析】【解答】解:根据题意,得: ,
在△ODP和△OCP中
∴
∴ ,即
∴画出OP的依据是:边边边,全等三角形对应角相等
故答案为:C.
【分析】根据SSS判断出△ODP≌△OCP,根据全等三角形的对应角相等得∠DOP=∠COP,据此即可得出答案.
2.【答案】C
【解析】【解答】A.∵,,
∴不能判定△ABC≌△XYZ,故本选项不符合题意;
B.,
∴不能判定△DEF≌△XYZ,故本选项不符合题意;
C.∵,,
∴,此本选项符合题意;
D.在△DEF中,,故本选项不符合题意.
故答案为:C.
【分析】利用全等三角形的判定方法和性质逐项判断即可。
3.【答案】A
【解析】【解答】解:AE和BD相交于点O,
,
在和中,∠A=∠B,
,
,
,
,
即,
在和中,
,
,
,
,
,
即的度数为,
故答案为:A.
【分析】先利用“AAS”证明,可得CE=DE,再利用角的运算求出,即可得到的度数为。
4.【答案】C
【解析】【解答】解:A、两个三角形周长相等,不能判断两个三角形全等,A选项不符合题意;
B、两个三角形三个内角分别相等,不能判断两个三角形全等,B选项不符合题意;
C、两个三角形有两条边和其中一条边上的中线分别相等,能够判断两个三角形全等,C选项符合题意;
D、两个三角形有两条边和一对角分别相等,不能判断两个三角形全等,D选项不符合题意.
故答案为:C.
【分析】周长相等的两个三角形的三边不一定对应相等,故两个三角形不一定全等,据此判断A;两个三角形三个内角分别相等,只能说明两个三角形的形状一定相等,大小不一定相等,故两个三角形不一定全等,据此判断B;根据三角形完全的判定方法“SSS”、“SAS”可判断有两条边和其中一条边上的中线分别相等的两个三角形全等,据此判断C;两条边对应相等且夹角相等的两个三角形才全等,据此判断D.
5.【答案】B
【解析】【解答】解:∵,
∴,
在 与 中,
,
∴,
∴, , ,
故答案为:B.
【分析】根据HL证明 ,利用全等三角形的性质进行判断即可.
6.【答案】A
【解析】【解答】解:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC与△ADE中,
,
∴△ABC≌△ADE(SAS),
在△ABC与△ADE中,
,
∴△ABC≌△ADE(ASA),
在△ABC与△ADE中,
,
∴△ABC≌△ADE(AAS),
故B、C、D选项正确符合题意,A选项不符合题意.
故答案为:A.
【分析】根据∠BAD=∠CAE结合角的和差关系可得∠BAC=∠DAE,由已知条件可知AC=AE,根据全等三角形的判定定理SAS可以添加AB=AD,根据全等三角形的判定定理ASA可以添加∠C=∠E,根据全等三角形的判定定理AAS可以添加∠B=∠D,从而即可一一判断得出答案.
7.【答案】C
【解析】【解答】∵AB=AC,∠A=∠A
∴当∠B=∠C时,由角边角的判定定理可知△ABE≌△ACD
故A不符合题意
当AD=AE时,由边角边的判定定理可知△ABE≌△ACD
故B不符合题意
当BE=CD时,没有边边角的判定定理,从而不能判定△ABE与△ACD全等
故C符合题意
当BD=CE时,则有AB-BD=AC-CE,即AD=AE,由边角边的判定定理可知△ABE≌△ACD
故D不符合题意
综上所述,满足题意的为选项 C
故答案为:C
【分析】要使△ABE≌△ACD,已知AB=AC,∠A=∠A,只需添加一对角相等或∠A的另一对邻边相等,据此逐一判断即可.
8.【答案】A
【解析】【解答】解:延长BE,AD交于点F,
∵AD∥BC,
∴∠CBA+∠BAD=180°,
∵AE平分∠BAD,BE平分∠CBA,
∴∠BAE= ∠BAD,∠ABE= ∠ABC,
∴∠BAE+∠ABE=90°,
∴∠AEB=90°,
故选项C不符合题意;
∵AD∥BC,
∴∠ABF=∠F,∠C=∠D,
∵AE平分∠BAD,
∴∠BAE=∠FAE,
∵AE=AE,
∴△ABE≌△AFE(AAS),
∴BE=EF,
∵∠C=∠D,∠BEC=∠FED,
∴△BCE≌△FDE(AAS),
∴CE=DE,
∴E为CD中点,
故选项B不符合题意;
∵△BCE≌△FDE,
∴S△ABF=S四边形ABCD,
∵E为CD中点,
∴S△ABE= S△ABF,
∴S△ABE= S四边形ABCD,
故选项D不符合题意;
∵△ABE≌△AFE(AAS),△BCE≌△FDE(AAS),
∴AB=AF,BC=DF,
∵AF=AD+DF=AD+BC,
∴AB=AD+BC,
∵AB与CD不一定相等,
∴BC+AD=CD不一定成立;
故选项A符合题意.
故答案为:A.
【分析】C、先根据二直线平行,同旁内角互补,得∠CBA+∠BAD=180°,再根据角平分线的定义得∠BAE+∠ABE=90°,从而根据三角形的内角和定理得∠AEB=90°,据此判断C选项;
B、延长BE,AD交于点F,先用AAS证明△ABE≌△AFE,根据全等三角形的性质得BE=EF,再用AAS证明△BCE≌△FDE,根据全等三角形的性质得CE=DE,即E为CD中点,据此判断B;
D、根据△BCE≌△FDE,得S△ABF=S四边形ABCD,再根据E为CD中点,得S△ABE=S△ABF,最后得S△ABE=S四边形ABCD,据此判断D;
A、由△ABE≌△AFE,△BCE≌△FDE,得AB=AF,BC=DF,再根据AF=AD+DF=AD+BC,得AB=AD+BC,因此BC+AD=CD不一定成立,据此判断A.
9.【答案】∠ADC=∠AEB
【解析】【解答】解:添加条件,理由如下:
在△ADC和△AEB中,
,
∴△ADC和△AEB(ASA),
故答案为:∠ADC=∠AEB.
【分析】题干已经给出了AD=AE,图形中有公共角∠DAC=∠EAB,要使用ASA判断△ADC和△AEB全等,只需要添加∠ADC=∠AEB.
10.【答案】ASA
【解析】【解答】解:由图得:遮挡住的三角形中露出两个角及其夹边.
则能画出与此直角三角形全等的三角形,其全等的依据是ASA.
故答案为:ASA.
【分析】由图得:遮挡住的三角形中露出两个角及其夹边,然后根据全等三角形的判定定理进行解答.
11.【答案】∠C=∠F或∠ABC=∠EDF或AC=EF
【解析】【解答】解:∵AD=BE,
∴AB=DE,
∵∠A=∠E,
当∠C=∠F时,△ABC≌△EDF(AAS);
当∠ABC=∠EDF时
△ABC≌△EDF(ASA);
当AC=EF时
△ABC≌△EDF(SAS);
故答案为:∠C=∠F或∠ABC=∠EDF或AC=EF
【分析】由AD=BE可证得AB=DE;已知一组角定对应相等,一边一角,可以添加另外两组角中的一组对应角相等,或添加AC=EF,即可求解.
12.【答案】90
【解析】【解答】解:如图,由题意得:,
,
,
,
,
,
故答案为:90.
【分析】先求出,再求出,最后求解即可。
13.【答案】证明:∵ ,
∴ ,即 ,
在 和 中,
∵ , , ,
∴ ,
∴ ,
∴.
【解析】【分析】由BE=CF,根据等量减去等量差相等推出BC=EF,从而用SAS判断出△ABC≌△DFE,由全等三角形的对应角相等得∠B=∠F,进而根据内错角相等,两直线平行,得AB∥DF.
14.【答案】解:已知:BC=AD,∠ABC=∠BAD,
求证:AC=BD.
证明:在△ABC和△BAD中,
∵,
∴,
∴,
即命题得证.
【解析】【分析】已知:BC=AD,∠ABC=∠BAD,求证:AC=BD;利用SAS易证△ABC≌△BAD,据此可得结论.
15.【答案】(1)解:如果,,,那么.
证明:∵,
∴,即,
在与中,
,
∴,
∴
【解析】【分析】如果AB=DE,∠ABC=∠DEF,BE=CF,那么AC=DF;根据线段的和差易得BC=EF,从而根据SAS证明△ABC≌△DEF,根据全等三角形对应边相等即可得出结论.
16.【答案】证明:
与都是直角三角形,
点是的中点,
,
在与中,
,
.
【解析】【分析】由题意可得△ABO、△DCO均为直角三角形,由中点的概念可得OB=OC,利用HL证明△ABO≌△DCO,据此可得结论.
17.【答案】证明:∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∵点E为AD中点,
∴BE=CE,
在△ABE与△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AB=CD.
【解析】【分析】先求出 ∠A=∠D,∠B=∠C, 再利用全等三角形的判定与性质证明即可。
18.【答案】证明:∵AB⊥BE,DE⊥BE,
∴∠B=∠E.
∵FB=CE,
∴FB+CF=CE+CF,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
【解析】【分析】根据垂直的概念可得∠B=∠E,由FB=CE以及线段的和差关系可得BC=EF,由已知条件可知AB=DE,利用SAS证明△ABC≌△DEF,据此可得结论.
19.【答案】证明:∵,,
∴,
在和中,
∵,,,
∴,
∴.
【解析】【分析】由已知条件结合线段的和差关系可得BE=BC,利用SAS证明△ABC≌△DBE,据此可得结论.
20.【答案】解:,,,
,
在和中,
,
∴(ASA),
,
米,米,
(米,
答:楼高是25米.
【解析】【分析】先利用三角形的内角和定理求得的度数证得,再通过ASA判定得到DP=AB,进而求得AB的长度.
一、单选题
1.如图是用直尺和圆规作已知角∠AOB平分线OP的示意图,仔细观察,根据三角形全等的知识,说明画出OP的依据是()
A.边角边,全等三角形对应角相等
B.角边角,全等三角形对应角相等
C.边边边,全等三角形对应角相等
D.斜边直角边,全等三角形对应角相等
2.已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A.△ABC≌△XYZ B.△DEF≌△XYZ
C. D.
3.如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )
A.71° B.76° C.78° D.80°
4.下列条件能够判断两个三角形全等的是( )
A.两个三角形周长相等
B.两个三角形三个内角分别相等
C.两个三角形有两条边和其中一条边上的中线分别相等
D.两个三角形有两条边和一对角分别相等
5.如图,在ABC中,AB=AC,AD⊥BC于点D,则下列结论,一定成立的是( )
A.BD=AD B.∠B=∠C
C.AD=CD D.∠BAD=∠ACD
6.如图,已知∠BAD=∠CAE,AC=AE,下列添加的条件中不能证明 是( )
A.DE=BC B.AB=AD C.∠C=∠E D.∠B=∠D
7.如图,点在上,点在上,已知,添加下列一个条件后仍无法判定的是( )
A. B. C. D.
8.如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE平分∠ABC,则以下命题不正确的是( )
A.BC+AD=CD B.E为CD中点
C.∠AEB=90° D.S△ABE=S四边形ABCD
二、填空题
9.如图,已知,请你添加一个条件,能运用直接说明≌,你添加的条件是
不添加任何字母和辅助线
10.如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是 .
11.如图,点A,D,B,E在同一条直线上,AD=BE,∠A =∠E ,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 .
12.如图,在由6个相同的小正方形拼成的网格中,∠2﹣∠1= °.
三、解答题
13.如图,点,,,在同一条直线上,,,.求证:.
14.如图,点D是△ABC外一点,连接BD、 AD,AD与BC交于点O.下列三个等式:①BC=AD;②∠ABC=∠BAD;③AC= BD.请从这三个等式中,任选两个作为已知条件,剩下的一个作为结论,组成一个真命题,将你选择的等式或等式的序号填在下面对应的横线上,然后对该真命题进行证明.
已知: ,
求证:
15.如图,在和中,B,E,C,F在同一直线上,下面给出四个论断:
(1); (2); (3); (4).
请把上述论断中的三个作为条件,余下的一个作为结论,写出一个真命题,并给出证明.
16.如图,已知,,垂足是的中点.求证:.
17.如图,AB∥CD,AD与BC相交于点E,若点E为AD中点,求证:AB=CD.
18.如图,点B、F、C、E在同一条直线上,AB⊥BE,DE⊥BE,AB=DE,BF=EC,求证:∠A=∠D.
19.如图,点E,C分别在边,上,已知,.求证:.
20.为了测量一幢高楼的高,在旗杆与楼之间选定一点.测得旗杆顶的视线与地面的夹角,测楼顶的视线与地面的夹角,量得点到楼底距离与旗杆高度相等,等于8米,量得旗杆与楼之间距离为米,求楼高是多少米?
答案解析部分
1.【答案】C
【解析】【解答】解:根据题意,得: ,
在△ODP和△OCP中
∴
∴ ,即
∴画出OP的依据是:边边边,全等三角形对应角相等
故答案为:C.
【分析】根据SSS判断出△ODP≌△OCP,根据全等三角形的对应角相等得∠DOP=∠COP,据此即可得出答案.
2.【答案】C
【解析】【解答】A.∵,,
∴不能判定△ABC≌△XYZ,故本选项不符合题意;
B.,
∴不能判定△DEF≌△XYZ,故本选项不符合题意;
C.∵,,
∴,此本选项符合题意;
D.在△DEF中,,故本选项不符合题意.
故答案为:C.
【分析】利用全等三角形的判定方法和性质逐项判断即可。
3.【答案】A
【解析】【解答】解:AE和BD相交于点O,
,
在和中,∠A=∠B,
,
,
,
,
即,
在和中,
,
,
,
,
,
即的度数为,
故答案为:A.
【分析】先利用“AAS”证明,可得CE=DE,再利用角的运算求出,即可得到的度数为。
4.【答案】C
【解析】【解答】解:A、两个三角形周长相等,不能判断两个三角形全等,A选项不符合题意;
B、两个三角形三个内角分别相等,不能判断两个三角形全等,B选项不符合题意;
C、两个三角形有两条边和其中一条边上的中线分别相等,能够判断两个三角形全等,C选项符合题意;
D、两个三角形有两条边和一对角分别相等,不能判断两个三角形全等,D选项不符合题意.
故答案为:C.
【分析】周长相等的两个三角形的三边不一定对应相等,故两个三角形不一定全等,据此判断A;两个三角形三个内角分别相等,只能说明两个三角形的形状一定相等,大小不一定相等,故两个三角形不一定全等,据此判断B;根据三角形完全的判定方法“SSS”、“SAS”可判断有两条边和其中一条边上的中线分别相等的两个三角形全等,据此判断C;两条边对应相等且夹角相等的两个三角形才全等,据此判断D.
5.【答案】B
【解析】【解答】解:∵,
∴,
在 与 中,
,
∴,
∴, , ,
故答案为:B.
【分析】根据HL证明 ,利用全等三角形的性质进行判断即可.
6.【答案】A
【解析】【解答】解:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC与△ADE中,
,
∴△ABC≌△ADE(SAS),
在△ABC与△ADE中,
,
∴△ABC≌△ADE(ASA),
在△ABC与△ADE中,
,
∴△ABC≌△ADE(AAS),
故B、C、D选项正确符合题意,A选项不符合题意.
故答案为:A.
【分析】根据∠BAD=∠CAE结合角的和差关系可得∠BAC=∠DAE,由已知条件可知AC=AE,根据全等三角形的判定定理SAS可以添加AB=AD,根据全等三角形的判定定理ASA可以添加∠C=∠E,根据全等三角形的判定定理AAS可以添加∠B=∠D,从而即可一一判断得出答案.
7.【答案】C
【解析】【解答】∵AB=AC,∠A=∠A
∴当∠B=∠C时,由角边角的判定定理可知△ABE≌△ACD
故A不符合题意
当AD=AE时,由边角边的判定定理可知△ABE≌△ACD
故B不符合题意
当BE=CD时,没有边边角的判定定理,从而不能判定△ABE与△ACD全等
故C符合题意
当BD=CE时,则有AB-BD=AC-CE,即AD=AE,由边角边的判定定理可知△ABE≌△ACD
故D不符合题意
综上所述,满足题意的为选项 C
故答案为:C
【分析】要使△ABE≌△ACD,已知AB=AC,∠A=∠A,只需添加一对角相等或∠A的另一对邻边相等,据此逐一判断即可.
8.【答案】A
【解析】【解答】解:延长BE,AD交于点F,
∵AD∥BC,
∴∠CBA+∠BAD=180°,
∵AE平分∠BAD,BE平分∠CBA,
∴∠BAE= ∠BAD,∠ABE= ∠ABC,
∴∠BAE+∠ABE=90°,
∴∠AEB=90°,
故选项C不符合题意;
∵AD∥BC,
∴∠ABF=∠F,∠C=∠D,
∵AE平分∠BAD,
∴∠BAE=∠FAE,
∵AE=AE,
∴△ABE≌△AFE(AAS),
∴BE=EF,
∵∠C=∠D,∠BEC=∠FED,
∴△BCE≌△FDE(AAS),
∴CE=DE,
∴E为CD中点,
故选项B不符合题意;
∵△BCE≌△FDE,
∴S△ABF=S四边形ABCD,
∵E为CD中点,
∴S△ABE= S△ABF,
∴S△ABE= S四边形ABCD,
故选项D不符合题意;
∵△ABE≌△AFE(AAS),△BCE≌△FDE(AAS),
∴AB=AF,BC=DF,
∵AF=AD+DF=AD+BC,
∴AB=AD+BC,
∵AB与CD不一定相等,
∴BC+AD=CD不一定成立;
故选项A符合题意.
故答案为:A.
【分析】C、先根据二直线平行,同旁内角互补,得∠CBA+∠BAD=180°,再根据角平分线的定义得∠BAE+∠ABE=90°,从而根据三角形的内角和定理得∠AEB=90°,据此判断C选项;
B、延长BE,AD交于点F,先用AAS证明△ABE≌△AFE,根据全等三角形的性质得BE=EF,再用AAS证明△BCE≌△FDE,根据全等三角形的性质得CE=DE,即E为CD中点,据此判断B;
D、根据△BCE≌△FDE,得S△ABF=S四边形ABCD,再根据E为CD中点,得S△ABE=S△ABF,最后得S△ABE=S四边形ABCD,据此判断D;
A、由△ABE≌△AFE,△BCE≌△FDE,得AB=AF,BC=DF,再根据AF=AD+DF=AD+BC,得AB=AD+BC,因此BC+AD=CD不一定成立,据此判断A.
9.【答案】∠ADC=∠AEB
【解析】【解答】解:添加条件,理由如下:
在△ADC和△AEB中,
,
∴△ADC和△AEB(ASA),
故答案为:∠ADC=∠AEB.
【分析】题干已经给出了AD=AE,图形中有公共角∠DAC=∠EAB,要使用ASA判断△ADC和△AEB全等,只需要添加∠ADC=∠AEB.
10.【答案】ASA
【解析】【解答】解:由图得:遮挡住的三角形中露出两个角及其夹边.
则能画出与此直角三角形全等的三角形,其全等的依据是ASA.
故答案为:ASA.
【分析】由图得:遮挡住的三角形中露出两个角及其夹边,然后根据全等三角形的判定定理进行解答.
11.【答案】∠C=∠F或∠ABC=∠EDF或AC=EF
【解析】【解答】解:∵AD=BE,
∴AB=DE,
∵∠A=∠E,
当∠C=∠F时,△ABC≌△EDF(AAS);
当∠ABC=∠EDF时
△ABC≌△EDF(ASA);
当AC=EF时
△ABC≌△EDF(SAS);
故答案为:∠C=∠F或∠ABC=∠EDF或AC=EF
【分析】由AD=BE可证得AB=DE;已知一组角定对应相等,一边一角,可以添加另外两组角中的一组对应角相等,或添加AC=EF,即可求解.
12.【答案】90
【解析】【解答】解:如图,由题意得:,
,
,
,
,
,
故答案为:90.
【分析】先求出,再求出,最后求解即可。
13.【答案】证明:∵ ,
∴ ,即 ,
在 和 中,
∵ , , ,
∴ ,
∴ ,
∴.
【解析】【分析】由BE=CF,根据等量减去等量差相等推出BC=EF,从而用SAS判断出△ABC≌△DFE,由全等三角形的对应角相等得∠B=∠F,进而根据内错角相等,两直线平行,得AB∥DF.
14.【答案】解:已知:BC=AD,∠ABC=∠BAD,
求证:AC=BD.
证明:在△ABC和△BAD中,
∵,
∴,
∴,
即命题得证.
【解析】【分析】已知:BC=AD,∠ABC=∠BAD,求证:AC=BD;利用SAS易证△ABC≌△BAD,据此可得结论.
15.【答案】(1)解:如果,,,那么.
证明:∵,
∴,即,
在与中,
,
∴,
∴
【解析】【分析】如果AB=DE,∠ABC=∠DEF,BE=CF,那么AC=DF;根据线段的和差易得BC=EF,从而根据SAS证明△ABC≌△DEF,根据全等三角形对应边相等即可得出结论.
16.【答案】证明:
与都是直角三角形,
点是的中点,
,
在与中,
,
.
【解析】【分析】由题意可得△ABO、△DCO均为直角三角形,由中点的概念可得OB=OC,利用HL证明△ABO≌△DCO,据此可得结论.
17.【答案】证明:∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∵点E为AD中点,
∴BE=CE,
在△ABE与△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AB=CD.
【解析】【分析】先求出 ∠A=∠D,∠B=∠C, 再利用全等三角形的判定与性质证明即可。
18.【答案】证明:∵AB⊥BE,DE⊥BE,
∴∠B=∠E.
∵FB=CE,
∴FB+CF=CE+CF,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
【解析】【分析】根据垂直的概念可得∠B=∠E,由FB=CE以及线段的和差关系可得BC=EF,由已知条件可知AB=DE,利用SAS证明△ABC≌△DEF,据此可得结论.
19.【答案】证明:∵,,
∴,
在和中,
∵,,,
∴,
∴.
【解析】【分析】由已知条件结合线段的和差关系可得BE=BC,利用SAS证明△ABC≌△DBE,据此可得结论.
20.【答案】解:,,,
,
在和中,
,
∴(ASA),
,
米,米,
(米,
答:楼高是25米.
【解析】【分析】先利用三角形的内角和定理求得的度数证得,再通过ASA判定得到DP=AB,进而求得AB的长度.
