2023-2024学年四川省宜宾市叙州重点中学高三(上)开学数学试卷(文科)(含解析)
文档属性
| 名称 | 2023-2024学年四川省宜宾市叙州重点中学高三(上)开学数学试卷(文科)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 436.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 15:13:35 | ||
图片预览



文档简介
2023-2024学年四川省宜宾市叙州重点中学高三(上)开学数学试卷(文科)
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知复数满足为虚数单位,则复数在复平面所对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知命题:,,则的否定为( )
A. , B. ,
C. , D. ,
3. 若,是任意实数,且,则( )
A. B. C. D.
4. 函数在处的切线方程为( )
A. B. C. D.
5. 密位制是度量角与弧的常用制度之一,周角的称为密位.用密位作为角的度量单位来度量角与弧的制度称为密位制.在密位制中,采用四个数字来记角的密位,且在百位数字与十位数字之间加一条短线,单位名称可以省去.如密位记为“”,个平角,个周角已知函数,,则函数的最小值用密位制表示为( )
A. B. C. D.
6. 已知实数,满足条件,则的最大值为( )
A. B. C. D.
7. 下列命题中错误的是( )
A. 在回归分析中,相关系数的绝对值越大,两个变量的线性相关性越强
B. 对分类变量与,它们的随机变量的观测值越小,说明“与有关系”的把握越大
C. 线性回归直线恒过样本中心
D. 在回归分析中,残差平方和越小,模型的拟合效果越好
8. 若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
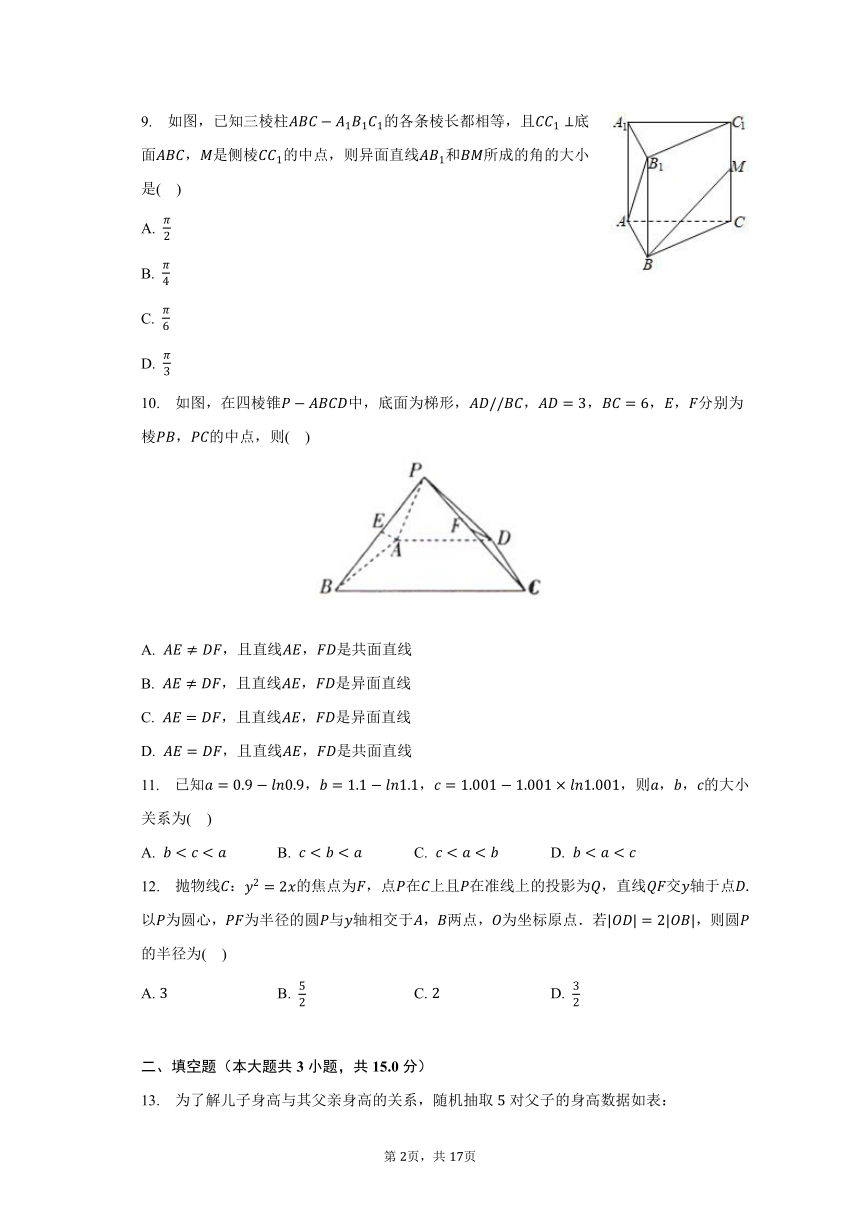
9. 如图,已知三棱柱的各条棱长都相等,且底面,是侧棱的中点,则异面直线和所成的角的大小是( )
A.
B.
C.
D.
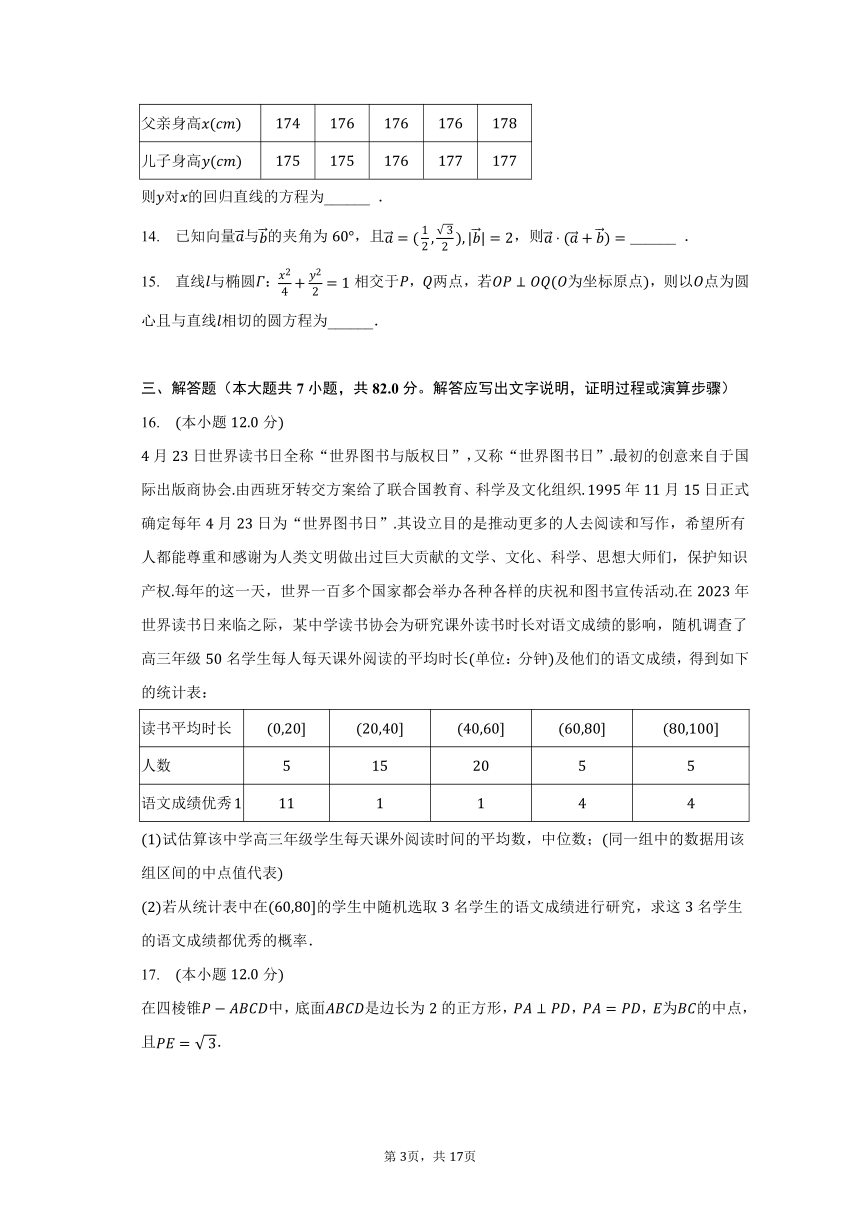
10. 如图,在四棱锥中,底面为梯形,,,,,分别为棱,的中点,则( )
A. ,且直线,是共面直线
B. ,且直线,是异面直线
C. ,且直线,是异面直线
D. ,且直线,是共面直线
11. 已知,,,则,,的大小关系为( )
A. B. C. D.
12. 抛物线:的焦点为,点在上且在准线上的投影为,直线交轴于点以为圆心,为半径的圆与轴相交于,两点,为坐标原点.若,则圆的半径为( )
A. B. C. D.
二、填空题(本大题共3小题,共15.0分)
13. 为了解儿子身高与其父亲身高的关系,随机抽取对父子的身高数据如表:
父亲身高
儿子身高
则对的回归直线的方程为______ .
14. 已知向量与的夹角为,且,则 ______ .
15. 直线与椭圆:相交于,两点,若为坐标原点,则以点为圆心且与直线相切的圆方程为______.
三、解答题(本大题共7小题,共82.0分。解答应写出文字说明,证明过程或演算步骤)
16. 本小题分
月日世界读书日全称“世界图书与版权日”,又称“世界图书日”最初的创意来自于国际出版商协会由西班牙转交方案给了联合国教育、科学及文化组织年月日正式确定每年月日为“世界图书日”其设立目的是推动更多的人去阅读和写作,希望所有人都能尊重和感谢为人类文明做出过巨大贡献的文学、文化、科学、思想大师们,保护知识产权每年的这一天,世界一百多个国家都会举办各种各样的庆祝和图书宣传活动在年世界读书日来临之际,某中学读书协会为研究课外读书时长对语文成绩的影响,随机调查了高三年级名学生每人每天课外阅读的平均时长单位:分钟及他们的语文成绩,得到如下的统计表:
读书平均时长
人数
语文成绩优秀
试估算该中学高三年级学生每天课外阅读时间的平均数,中位数;同一组中的数据用该组区间的中点值代表
若从统计表中在的学生中随机选取名学生的语文成绩进行研究,求这名学生的语文成绩都优秀的概率.
17. 本小题分
在四棱锥中,底面是边长为的正方形,,,为的中点,且.
求证:平面;
求四棱锥的体积.
18. 本小题分
已知函数.
当时,求函数的极值;
若函数在区间上单调递增,求实数的取值范围.
19. 本小题分
已知为坐标原点,椭圆的离心率为,椭圆的上顶点到右顶点的距离为.
求椭圆的方程;
若椭圆的左、右顶点分别为、,过点作直线与椭圆交于、两点,且、位于第一象限,在线段上,直线与直线相交于点,连接、,直线、的斜率分别记为、,求的值.
20. 本小题分
设函数,其中为自然对数的底数.
若曲线在轴上的截距为,且在点处的切线垂直于直线,求实数,的值;
记的导函数为,在区间上的最小值为,求的最大值.
21. 本小题分
在直角坐标系中,直线的方程为,曲线的参数方程为参数
Ⅰ已知在极坐标系与直角坐标系取相同的长度单位,且以原点为极点,以轴正半轴为极轴中,点的极坐标,判断点与直线的位置关系;
Ⅱ设点为曲线上的一个动点,求它到直线的距离的最小值.
22. 本小题分
设.
解不等式;
已知实数、、满足,且的最大值是,求的值.
答案和解析
1.【答案】
【解析】解:,
复数满足为虚数单位,
,
,
解得,
,
则复数在复平面所对应的点在第二象限.
故选:.
设,由于复数满足为虚数单位,可得,于是,解出即可.
本题考查了复数的模的计算公式、复数相等、几何意义,考查了推理能力与计算能力,属于基础题.
2.【答案】
【解析】【分析】
本题主要考查全称量词命题的否定,属于基础题.
根据全称量词命题的否定即可得到结论.
【解答】
解:命题为全称量词命题,则命题的否定为,,
故选D.
3.【答案】
【解析】解:根据题意,依次分析选项:
对于,当,时,满足,但,A错误;
对于,当,时,满足,但,B错误;
对于,当,时,,C错误;
对于,函数在上为减函数,若,必有在成立,D正确.
故选:.
根据题意,由不等式的性质依次分析选项,综合可得答案.
本题考查不等式的性质,涉及不等式的证明,属于基础题.
4.【答案】
【解析】解:时,,函数的导数为,
在点处的切线的斜率为,
则函数在点处的切线方程为.
故选:.
求得函数的导数,可得切线的斜率,由斜截式方程可得切线方程.
本题考查导数的运用:求切线方程,考查方程思想和运算能力,属于基础题.
5.【答案】
【解析】解:根据题意,,,
其导数,
在区间上,,为增函数,
在区间上,,为减函数,
且,,则的最小值为,
其密位大小为,用密位制表示为;
故选:.
根据题意,利用导数求出,的最小值,进而用密位制表示,即可得答案.
本题考查函数的最值,关键掌握密位制表示角的方法,属于基础题.
6.【答案】
【解析】解:由约束条件作出可行域如图,
联立,解得.
化为,由图可知,当直线过时,
直线在轴上的截距最大,有最大值为.
故选:.
由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.
7.【答案】
【解析】解:对于选项A:在回归分析中,对于相关系数,当越接近时,相关程度越大,说明拟合效果越好,故选项A正确;
对于选项B:对于分类变量与,它们的随机变量的观测值越小,说明“与有关系”的可能性越小,故选项B错误;
对于选项C:已知线性回归直线,
其中,
所以回归直线恒过样本中心,故选项C正确;
对于选项D:在回归分析中,残差平方和越小,模型的拟合效果越好,故选项D正确.
故选:.
由题意,根据线性回归方程、相关系数的定义、独立性检验以及残差平方和对选项进行逐一分析,进而即可求解.
本题考查线性回归方程、相关系数、独立性检验等,考查了逻辑推理能力.
8.【答案】
【解析】解:,由题意在上恒成立.
若,显然有;
若,由得,于是,
,
综上知.
故选:.
求出,分两种情况当小于等于时,导函数恒小于满足题意;当大于,根据导函数小于等于列出不等式,求出的取值范围,让的最大值大于列出关于的不等式,求出的取值范围,两者求出并集即可得到所有满足题意的范围.
此题要求学生会利用导函数的正负研究函数的单调性,是一道中档题.
9.【答案】
【解析】【分析】
本题考查了向量的夹角公式、数量积运算与向量垂直的关系,属于基础题.
如图所示,建立空间直角坐标系.利用向量的夹角公式、数量积运算即可得出.
【解答】
解:如图所示,建立空间直角坐标系.
令,则,,,
.
,.
.
.
异面直线和所成的角是.
故选:.
10.【答案】
【解析】解:如图,连接,
,分别为棱,的中点,,,,
,,
,且,
四边形是平行四边形,
,且,
,是共面直线.
故选:.
可连接,根据条件即可说明四边形是平行四边形,从而得出,且直线,是共面直线.
本题考查了平行四边形的定义,中位线的性质,两条平行线共面,考查了推理能力,属于基础题.
11.【答案】
【解析】解:设,,则有,
所以当时,,单调递减;
当时,,单调递增.
所以,,即有,.
令,则,
所以当时,,单调递增;
当时,,单调递减.
所以,即,故,,
令,有,
可得函数单调递增,故有,可得,
可得,故,综上所述,.
故选:.
设,,利用导函数可得,的单调性,可得,,令,利用导函数可得在单调递增,从而有,即可得出答案.
本题考查了导数与单调性关系在函数值大小比较中的应用,属于中档题.
12.【答案】
【解析】解:设,由题意可得在准线上,所以为的中点,所以,
因为,所以为的中点,所以,所以,,
因为为圆上,所以可得:,解得:,所以圆的半径为:
故选:.
设的坐标,由题意可得的坐标,可得,的坐标,再由圆可得,解得的坐标,进而可得的半径.
本题考查抛物线的性质,属于中档题.
13.【答案】
【解析】【分析】
本题考查回归分析的初步应用,写方程要用的斜率和,的平均数都要经过计算算出,属于基础题.
根据所给的数据计算出,的平均数和回归直线的斜率,即可写出回归直线方程.
【解答】
解:,
,
样本组数据的样本中心点是,
,,
回归直线方程为.
故答案为:.
14.【答案】
【解析】解:,,
,
.
故答案为:.
根据条件可求出,然后进行数量积的运算即可求出的值.
本题考查了向量数量积的运算及计算公式,根据向量的坐标求向量的长度的方法,考查了计算能力,属于基础题.
15.【答案】
【解析】解:当直线的斜率不存在,设的坐标为,,
若,结合椭圆的对称性分析可得,则直线方程为,代入椭圆方程,解得:,
以点为圆心且与直线相切的圆方程,
当直线的斜率存在时且不为,设,直线的方程为,
由,整理得,,,
由,则,即,即,
,
成立,
因为与圆心为的定圆相切 所以到的距离,
即定圆的方程为.
综上可知:以点为圆心且与直线相切的圆方程,
故答案为:.
分类讨论,当直线的斜率存在时,设直线的方程,代入椭圆方程,由韦达定理及向量的坐标运算,
本题考查直线与椭圆的位置关系,考查韦达定理及向量的坐标运算,点到直线的距离公式的应用,考查计算能力,属于中档题.
16.【答案】解:该中学高三年级学生每天课外阅读时间的平均数为:
,
设中学高三年级学生每天课外阅读时间的中位数为,
所以,解得,
所以该中学高三年级学生每天课外阅读时间的中位数为;
区间的学生有人,记为,,,,,其中,,,为语文成绩优秀,
从中任取人,基本事件有:,,,,,,,,,,共种,
这名学生的语文成绩都优秀的为:,,,,共种,
故所求的概率为.
【解析】根据平均数和中位数的定义计算即可;
利用列举法写出基本事件,计算所求的概率值.
本题考查了平均数与中位数的计算问题,也考查了古典概率的计算问题,是基础题.
17.【答案】证明:取的中点,连接,,
,,,,得.
,分别为,的中点,.
由,得,
又,
平面,而平面,则,
又,平面;
解:由得,平面,
而平面,则平面平面.
在平面内,过点作,垂足为,则平面.
由知,,又,,
,从而,
,
则四棱锥的体积为.
【解析】取的中点,连接,,求解三角形可得,再证明平面,可得,从而得到平面;
由得,平面,可得平面平面在平面内,过点作,垂足为,则平面由已知求解,进一步求四棱锥的体积.
本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,考查多面体体积的求法,是中档题.
18.【答案】解:函数的定义域为,
当时,
求导得,
整理得:.
令可得,或舍去
当时,,函数在上单调递减,
当时,,函数在上单调递增,
所以当时,函数取极小值,极小值为,
函数无极大值;
由已知时,恒成立,
所以恒成立,
即恒成立,则.
令函数,
由知在单调递增,
从而.
经检验知,当时,函数不是常函数,
所以的取值范围是.
【解析】先求函数的定义域和导函数,根据导数与极值点的关系求极值点,再求极值即可;
由条件可知在上恒成立,再分离变量求最值即可求解.
本题考查导数的综合应用,利用导数研究函数的单调性与极值,化归转化思想,属中档题.
19.【答案】解:由题意知,,可得,
圆的上顶点到右顶点的距离为,
解得,,,
因此,椭圆的方程为;
解:如下图所示:
不妨设、,由图可知,直线的斜率存在,
设直线的方程为,因为点,则,则,
联立,可得,
,可得,即,
解得,
,,
解得,
所以,,易知、,
由于在直线上,设,
又由于在直线上,则,可得,
所以
.
【解析】由已知条件可得出关于、、的方程组,解出这三个量的值,即可得出椭圆的方程;
不妨设、,设直线的方程为,可得,将直线的方程与椭圆方程联立,列出韦达定理,设,根据点在直线上,得出,然后利用斜率公式以及韦达定理可求出的值.
本题考查椭圆方程的求法及直线与椭圆的综合应用,属于中档题.
20.【答案】解:曲线在轴上的截距为,则过点,代入,
则,则,求导,
由,即,则,
实数,的值分别为,;
,,,
当时,,,恒成立,
即,在上单调递增,
.
当时,,,恒成立,
即,在单调递减,
.
当时,,得,在上单调递减,在上单调递增,
所以,
,
当时,,
当时,,求导,,
由时,,
单调通减,,
当时,,单调递减,,
的最大值.
【解析】利用导数求切线的斜率;利用导数求函数的最值即可.
本题考查导数的综合应用.
21.【答案】解:Ⅰ把极坐标系下的点化为直角坐标,得分
因为点的直角坐标满足直线的方程,
所以点在直线上.分
因为点在曲线上,故可设点的坐标为,分
从而点到直线的距离为
,分
由此得,当时,取得最小值分
【解析】Ⅰ首先把点的极坐标转化成直角坐标,进一步利用点和方程的关系求出结果.
Ⅱ进一步利用点到直线的距离,利用三角函数关系式的恒等变换,把函数关系式变形成余弦型函数,进一步求出最值.
本题考查的知识要点:极坐标和直角坐标的互化,点到直线的距离的公式的应用,三角函数的最值问题.
22.【答案】解:时,不等式化为,,;
时,不等式化为,成立;
时,不等式化为,,;
综上所述,不等式的解集为;
由柯西不等式:,
因为,所以,
因为的最大值是,所以,
当时,取最大值,所以.
【解析】利用绝对值的意义,分类讨论,即可解不等式;
由柯西不等式:,可得出,从而可根据最大值为,建立关于的方程解出值即可.
本小题主要考查柯西不等式等基础知识,考查运算求解能力,对于柯西不等式的构造是题目的关键,需要同学们灵活应用.
第1页,共1页
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知复数满足为虚数单位,则复数在复平面所对应的点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知命题:,,则的否定为( )
A. , B. ,
C. , D. ,
3. 若,是任意实数,且,则( )
A. B. C. D.
4. 函数在处的切线方程为( )
A. B. C. D.
5. 密位制是度量角与弧的常用制度之一,周角的称为密位.用密位作为角的度量单位来度量角与弧的制度称为密位制.在密位制中,采用四个数字来记角的密位,且在百位数字与十位数字之间加一条短线,单位名称可以省去.如密位记为“”,个平角,个周角已知函数,,则函数的最小值用密位制表示为( )
A. B. C. D.
6. 已知实数,满足条件,则的最大值为( )
A. B. C. D.
7. 下列命题中错误的是( )
A. 在回归分析中,相关系数的绝对值越大,两个变量的线性相关性越强
B. 对分类变量与,它们的随机变量的观测值越小,说明“与有关系”的把握越大
C. 线性回归直线恒过样本中心
D. 在回归分析中,残差平方和越小,模型的拟合效果越好
8. 若函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
9. 如图,已知三棱柱的各条棱长都相等,且底面,是侧棱的中点,则异面直线和所成的角的大小是( )
A.
B.
C.
D.
10. 如图,在四棱锥中,底面为梯形,,,,,分别为棱,的中点,则( )
A. ,且直线,是共面直线
B. ,且直线,是异面直线
C. ,且直线,是异面直线
D. ,且直线,是共面直线
11. 已知,,,则,,的大小关系为( )
A. B. C. D.
12. 抛物线:的焦点为,点在上且在准线上的投影为,直线交轴于点以为圆心,为半径的圆与轴相交于,两点,为坐标原点.若,则圆的半径为( )
A. B. C. D.
二、填空题(本大题共3小题,共15.0分)
13. 为了解儿子身高与其父亲身高的关系,随机抽取对父子的身高数据如表:
父亲身高
儿子身高
则对的回归直线的方程为______ .
14. 已知向量与的夹角为,且,则 ______ .
15. 直线与椭圆:相交于,两点,若为坐标原点,则以点为圆心且与直线相切的圆方程为______.
三、解答题(本大题共7小题,共82.0分。解答应写出文字说明,证明过程或演算步骤)
16. 本小题分
月日世界读书日全称“世界图书与版权日”,又称“世界图书日”最初的创意来自于国际出版商协会由西班牙转交方案给了联合国教育、科学及文化组织年月日正式确定每年月日为“世界图书日”其设立目的是推动更多的人去阅读和写作,希望所有人都能尊重和感谢为人类文明做出过巨大贡献的文学、文化、科学、思想大师们,保护知识产权每年的这一天,世界一百多个国家都会举办各种各样的庆祝和图书宣传活动在年世界读书日来临之际,某中学读书协会为研究课外读书时长对语文成绩的影响,随机调查了高三年级名学生每人每天课外阅读的平均时长单位:分钟及他们的语文成绩,得到如下的统计表:
读书平均时长
人数
语文成绩优秀
试估算该中学高三年级学生每天课外阅读时间的平均数,中位数;同一组中的数据用该组区间的中点值代表
若从统计表中在的学生中随机选取名学生的语文成绩进行研究,求这名学生的语文成绩都优秀的概率.
17. 本小题分
在四棱锥中,底面是边长为的正方形,,,为的中点,且.
求证:平面;
求四棱锥的体积.
18. 本小题分
已知函数.
当时,求函数的极值;
若函数在区间上单调递增,求实数的取值范围.
19. 本小题分
已知为坐标原点,椭圆的离心率为,椭圆的上顶点到右顶点的距离为.
求椭圆的方程;
若椭圆的左、右顶点分别为、,过点作直线与椭圆交于、两点,且、位于第一象限,在线段上,直线与直线相交于点,连接、,直线、的斜率分别记为、,求的值.
20. 本小题分
设函数,其中为自然对数的底数.
若曲线在轴上的截距为,且在点处的切线垂直于直线,求实数,的值;
记的导函数为,在区间上的最小值为,求的最大值.
21. 本小题分
在直角坐标系中,直线的方程为,曲线的参数方程为参数
Ⅰ已知在极坐标系与直角坐标系取相同的长度单位,且以原点为极点,以轴正半轴为极轴中,点的极坐标,判断点与直线的位置关系;
Ⅱ设点为曲线上的一个动点,求它到直线的距离的最小值.
22. 本小题分
设.
解不等式;
已知实数、、满足,且的最大值是,求的值.
答案和解析
1.【答案】
【解析】解:,
复数满足为虚数单位,
,
,
解得,
,
则复数在复平面所对应的点在第二象限.
故选:.
设,由于复数满足为虚数单位,可得,于是,解出即可.
本题考查了复数的模的计算公式、复数相等、几何意义,考查了推理能力与计算能力,属于基础题.
2.【答案】
【解析】【分析】
本题主要考查全称量词命题的否定,属于基础题.
根据全称量词命题的否定即可得到结论.
【解答】
解:命题为全称量词命题,则命题的否定为,,
故选D.
3.【答案】
【解析】解:根据题意,依次分析选项:
对于,当,时,满足,但,A错误;
对于,当,时,满足,但,B错误;
对于,当,时,,C错误;
对于,函数在上为减函数,若,必有在成立,D正确.
故选:.
根据题意,由不等式的性质依次分析选项,综合可得答案.
本题考查不等式的性质,涉及不等式的证明,属于基础题.
4.【答案】
【解析】解:时,,函数的导数为,
在点处的切线的斜率为,
则函数在点处的切线方程为.
故选:.
求得函数的导数,可得切线的斜率,由斜截式方程可得切线方程.
本题考查导数的运用:求切线方程,考查方程思想和运算能力,属于基础题.
5.【答案】
【解析】解:根据题意,,,
其导数,
在区间上,,为增函数,
在区间上,,为减函数,
且,,则的最小值为,
其密位大小为,用密位制表示为;
故选:.
根据题意,利用导数求出,的最小值,进而用密位制表示,即可得答案.
本题考查函数的最值,关键掌握密位制表示角的方法,属于基础题.
6.【答案】
【解析】解:由约束条件作出可行域如图,
联立,解得.
化为,由图可知,当直线过时,
直线在轴上的截距最大,有最大值为.
故选:.
由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.
7.【答案】
【解析】解:对于选项A:在回归分析中,对于相关系数,当越接近时,相关程度越大,说明拟合效果越好,故选项A正确;
对于选项B:对于分类变量与,它们的随机变量的观测值越小,说明“与有关系”的可能性越小,故选项B错误;
对于选项C:已知线性回归直线,
其中,
所以回归直线恒过样本中心,故选项C正确;
对于选项D:在回归分析中,残差平方和越小,模型的拟合效果越好,故选项D正确.
故选:.
由题意,根据线性回归方程、相关系数的定义、独立性检验以及残差平方和对选项进行逐一分析,进而即可求解.
本题考查线性回归方程、相关系数、独立性检验等,考查了逻辑推理能力.
8.【答案】
【解析】解:,由题意在上恒成立.
若,显然有;
若,由得,于是,
,
综上知.
故选:.
求出,分两种情况当小于等于时,导函数恒小于满足题意;当大于,根据导函数小于等于列出不等式,求出的取值范围,让的最大值大于列出关于的不等式,求出的取值范围,两者求出并集即可得到所有满足题意的范围.
此题要求学生会利用导函数的正负研究函数的单调性,是一道中档题.
9.【答案】
【解析】【分析】
本题考查了向量的夹角公式、数量积运算与向量垂直的关系,属于基础题.
如图所示,建立空间直角坐标系.利用向量的夹角公式、数量积运算即可得出.
【解答】
解:如图所示,建立空间直角坐标系.
令,则,,,
.
,.
.
.
异面直线和所成的角是.
故选:.
10.【答案】
【解析】解:如图,连接,
,分别为棱,的中点,,,,
,,
,且,
四边形是平行四边形,
,且,
,是共面直线.
故选:.
可连接,根据条件即可说明四边形是平行四边形,从而得出,且直线,是共面直线.
本题考查了平行四边形的定义,中位线的性质,两条平行线共面,考查了推理能力,属于基础题.
11.【答案】
【解析】解:设,,则有,
所以当时,,单调递减;
当时,,单调递增.
所以,,即有,.
令,则,
所以当时,,单调递增;
当时,,单调递减.
所以,即,故,,
令,有,
可得函数单调递增,故有,可得,
可得,故,综上所述,.
故选:.
设,,利用导函数可得,的单调性,可得,,令,利用导函数可得在单调递增,从而有,即可得出答案.
本题考查了导数与单调性关系在函数值大小比较中的应用,属于中档题.
12.【答案】
【解析】解:设,由题意可得在准线上,所以为的中点,所以,
因为,所以为的中点,所以,所以,,
因为为圆上,所以可得:,解得:,所以圆的半径为:
故选:.
设的坐标,由题意可得的坐标,可得,的坐标,再由圆可得,解得的坐标,进而可得的半径.
本题考查抛物线的性质,属于中档题.
13.【答案】
【解析】【分析】
本题考查回归分析的初步应用,写方程要用的斜率和,的平均数都要经过计算算出,属于基础题.
根据所给的数据计算出,的平均数和回归直线的斜率,即可写出回归直线方程.
【解答】
解:,
,
样本组数据的样本中心点是,
,,
回归直线方程为.
故答案为:.
14.【答案】
【解析】解:,,
,
.
故答案为:.
根据条件可求出,然后进行数量积的运算即可求出的值.
本题考查了向量数量积的运算及计算公式,根据向量的坐标求向量的长度的方法,考查了计算能力,属于基础题.
15.【答案】
【解析】解:当直线的斜率不存在,设的坐标为,,
若,结合椭圆的对称性分析可得,则直线方程为,代入椭圆方程,解得:,
以点为圆心且与直线相切的圆方程,
当直线的斜率存在时且不为,设,直线的方程为,
由,整理得,,,
由,则,即,即,
,
成立,
因为与圆心为的定圆相切 所以到的距离,
即定圆的方程为.
综上可知:以点为圆心且与直线相切的圆方程,
故答案为:.
分类讨论,当直线的斜率存在时,设直线的方程,代入椭圆方程,由韦达定理及向量的坐标运算,
本题考查直线与椭圆的位置关系,考查韦达定理及向量的坐标运算,点到直线的距离公式的应用,考查计算能力,属于中档题.
16.【答案】解:该中学高三年级学生每天课外阅读时间的平均数为:
,
设中学高三年级学生每天课外阅读时间的中位数为,
所以,解得,
所以该中学高三年级学生每天课外阅读时间的中位数为;
区间的学生有人,记为,,,,,其中,,,为语文成绩优秀,
从中任取人,基本事件有:,,,,,,,,,,共种,
这名学生的语文成绩都优秀的为:,,,,共种,
故所求的概率为.
【解析】根据平均数和中位数的定义计算即可;
利用列举法写出基本事件,计算所求的概率值.
本题考查了平均数与中位数的计算问题,也考查了古典概率的计算问题,是基础题.
17.【答案】证明:取的中点,连接,,
,,,,得.
,分别为,的中点,.
由,得,
又,
平面,而平面,则,
又,平面;
解:由得,平面,
而平面,则平面平面.
在平面内,过点作,垂足为,则平面.
由知,,又,,
,从而,
,
则四棱锥的体积为.
【解析】取的中点,连接,,求解三角形可得,再证明平面,可得,从而得到平面;
由得,平面,可得平面平面在平面内,过点作,垂足为,则平面由已知求解,进一步求四棱锥的体积.
本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,考查多面体体积的求法,是中档题.
18.【答案】解:函数的定义域为,
当时,
求导得,
整理得:.
令可得,或舍去
当时,,函数在上单调递减,
当时,,函数在上单调递增,
所以当时,函数取极小值,极小值为,
函数无极大值;
由已知时,恒成立,
所以恒成立,
即恒成立,则.
令函数,
由知在单调递增,
从而.
经检验知,当时,函数不是常函数,
所以的取值范围是.
【解析】先求函数的定义域和导函数,根据导数与极值点的关系求极值点,再求极值即可;
由条件可知在上恒成立,再分离变量求最值即可求解.
本题考查导数的综合应用,利用导数研究函数的单调性与极值,化归转化思想,属中档题.
19.【答案】解:由题意知,,可得,
圆的上顶点到右顶点的距离为,
解得,,,
因此,椭圆的方程为;
解:如下图所示:
不妨设、,由图可知,直线的斜率存在,
设直线的方程为,因为点,则,则,
联立,可得,
,可得,即,
解得,
,,
解得,
所以,,易知、,
由于在直线上,设,
又由于在直线上,则,可得,
所以
.
【解析】由已知条件可得出关于、、的方程组,解出这三个量的值,即可得出椭圆的方程;
不妨设、,设直线的方程为,可得,将直线的方程与椭圆方程联立,列出韦达定理,设,根据点在直线上,得出,然后利用斜率公式以及韦达定理可求出的值.
本题考查椭圆方程的求法及直线与椭圆的综合应用,属于中档题.
20.【答案】解:曲线在轴上的截距为,则过点,代入,
则,则,求导,
由,即,则,
实数,的值分别为,;
,,,
当时,,,恒成立,
即,在上单调递增,
.
当时,,,恒成立,
即,在单调递减,
.
当时,,得,在上单调递减,在上单调递增,
所以,
,
当时,,
当时,,求导,,
由时,,
单调通减,,
当时,,单调递减,,
的最大值.
【解析】利用导数求切线的斜率;利用导数求函数的最值即可.
本题考查导数的综合应用.
21.【答案】解:Ⅰ把极坐标系下的点化为直角坐标,得分
因为点的直角坐标满足直线的方程,
所以点在直线上.分
因为点在曲线上,故可设点的坐标为,分
从而点到直线的距离为
,分
由此得,当时,取得最小值分
【解析】Ⅰ首先把点的极坐标转化成直角坐标,进一步利用点和方程的关系求出结果.
Ⅱ进一步利用点到直线的距离,利用三角函数关系式的恒等变换,把函数关系式变形成余弦型函数,进一步求出最值.
本题考查的知识要点:极坐标和直角坐标的互化,点到直线的距离的公式的应用,三角函数的最值问题.
22.【答案】解:时,不等式化为,,;
时,不等式化为,成立;
时,不等式化为,,;
综上所述,不等式的解集为;
由柯西不等式:,
因为,所以,
因为的最大值是,所以,
当时,取最大值,所以.
【解析】利用绝对值的意义,分类讨论,即可解不等式;
由柯西不等式:,可得出,从而可根据最大值为,建立关于的方程解出值即可.
本小题主要考查柯西不等式等基础知识,考查运算求解能力,对于柯西不等式的构造是题目的关键,需要同学们灵活应用.
第1页,共1页
同课章节目录
