数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
2.2.3 直线的一般式方程
学习目标
本节课的主要知识要素是推导并掌握直线的一般式方程,明确二元一次方程与直线的方程之间的关系;体会探究过程中的转化思想;教学过程中主要培养学生数学抽象,逻辑推理和数学运算的能力。
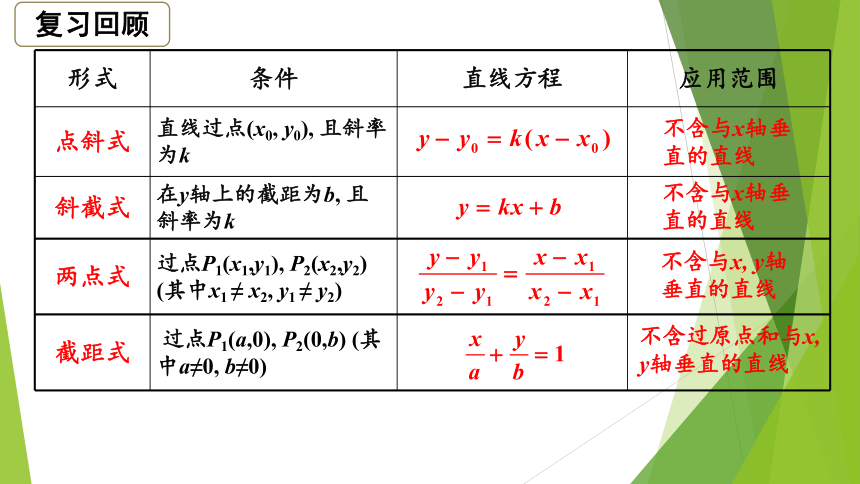
形式 条件 直线方程 应用范围
点斜式
斜截式
两点式
截距式
复习回顾
形式 条件 直线方程 应用范围
点斜式 直线过点(x0, y0), 且斜率为k
斜截式 在y轴上的截距为b, 且斜率为k
两点式 过点P1(x1,y1), P2(x2,y2) (其中x1 ≠ x2, y1 ≠ y2)
截距式 过点P1(a,0), P2(0,b) (其中a≠0, b≠0)
不含与x轴垂直的直线
不含与x轴垂直的直线
不含与x, y轴垂直的直线
不含过原点和与x, y轴垂直的直线
复习回顾
观察直线的点斜式、斜截式、两点式、截距式方程,我们发现,它们都是关于x,y的二元一次方程。
直线与一元二次方程是否都有这种关系呢?
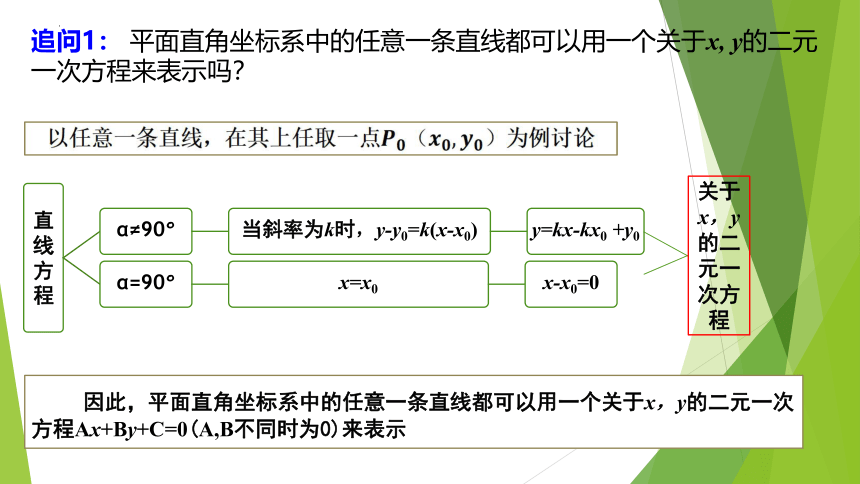
问题1:能否用一种方程形式表示平面直角坐标系中的任何一条直线
关于x,y的二元一次方程
因此,平面直角坐标系中的任意一条直线都可以用一个关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)来表示
追问1: 平面直角坐标系中的任意一条直线都可以用一个关于x, y的二元一次方程来表示吗?
由以上可知,关于x,y的二元一次方程都表示一条直线。
追问2: 任意一个关于x,y的二元一次方程都表示一条直线吗?
我们把关于x,y的二元一次方程
(其中A,B不同时为0)叫做直线的一般式方程,简称一般式。
Ax+By+C=0
探究
问题3在方程Ax+By+C=0中,A,B,C为何值时,方程表示如下直线:
①平行于x轴?
②平行于y轴?
③与x轴重合?
④与y轴重合?
A=0,B≠0,C=0 直线方程:y=0
A≠0,B=0,C=0 直线方程:x=0
例题
化为一般式,得 4x+3y-12=0
注意 : 对于直线方程的一般式,规定:
1)x的系数为正;
2)x,y的系数及常数项一般不出现分数;
3)按含x项,含y项、常数项顺序排列.
例6 把直线l的一般式方程x-2y+6=0化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
课本例题
在直角坐标系中画直线时,通常找出直线与两点坐标轴的交点,然后连接这两个点。
拓广探索
直线
试讨论:(1) 的条件是什么?
(2) 的条件是什么?
1.根据下列条件,写出直线的方程,并把它化成一般式:
(1)经过点A(8,-2),斜率是-
(2)经过点B(4,2),平行于x轴;
(3)经过点P1(3,-2),P2(5,-4);
(4)在x轴, y轴上的截距分别是
巩固练习
答案:(1) x+2y-4=0;(2) y-2=0;(3) x+y-1=0;(4) 2x-y-3=0
2.三角形ABC的三个顶点是A(4,0), B(6,7), C(0,3),求:
(1)边BC上的中线所在直线的方程;
(2)边BC上的高所在直线的方程;
(3)边BC的垂直平分线的方程;
巩固练习
答案:(1) 5x+y-20=0;(2) 3x+2y-12=0 ;(3)3x+2y-19=0
3.已知两条直线,求: 5x+5my+6=0, : (m-2)x+15y+2m=0
(1)当m为何值时,与垂直?
(2)当m为何值时,与平行?
巩固练习
答案:(1)因为 与垂直,所以有5 (m-2) -75m=0,解得m=;
(2)因为与平行,所以有解得m=5
课堂小结
(1)直线的一般式方程:Ax+By+C=0 (A,B不同时为0)
(2)Ax+By+C=0 (A,B不同时为0)
感谢观看
2.2.3 直线的一般式方程
学习目标
本节课的主要知识要素是推导并掌握直线的一般式方程,明确二元一次方程与直线的方程之间的关系;体会探究过程中的转化思想;教学过程中主要培养学生数学抽象,逻辑推理和数学运算的能力。
形式 条件 直线方程 应用范围
点斜式
斜截式
两点式
截距式
复习回顾
形式 条件 直线方程 应用范围
点斜式 直线过点(x0, y0), 且斜率为k
斜截式 在y轴上的截距为b, 且斜率为k
两点式 过点P1(x1,y1), P2(x2,y2) (其中x1 ≠ x2, y1 ≠ y2)
截距式 过点P1(a,0), P2(0,b) (其中a≠0, b≠0)
不含与x轴垂直的直线
不含与x轴垂直的直线
不含与x, y轴垂直的直线
不含过原点和与x, y轴垂直的直线
复习回顾
观察直线的点斜式、斜截式、两点式、截距式方程,我们发现,它们都是关于x,y的二元一次方程。
直线与一元二次方程是否都有这种关系呢?
问题1:能否用一种方程形式表示平面直角坐标系中的任何一条直线
关于x,y的二元一次方程
因此,平面直角坐标系中的任意一条直线都可以用一个关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)来表示
追问1: 平面直角坐标系中的任意一条直线都可以用一个关于x, y的二元一次方程来表示吗?
由以上可知,关于x,y的二元一次方程都表示一条直线。
追问2: 任意一个关于x,y的二元一次方程都表示一条直线吗?
我们把关于x,y的二元一次方程
(其中A,B不同时为0)叫做直线的一般式方程,简称一般式。
Ax+By+C=0
探究
问题3在方程Ax+By+C=0中,A,B,C为何值时,方程表示如下直线:
①平行于x轴?
②平行于y轴?
③与x轴重合?
④与y轴重合?
A=0,B≠0,C=0 直线方程:y=0
A≠0,B=0,C=0 直线方程:x=0
例题
化为一般式,得 4x+3y-12=0
注意 : 对于直线方程的一般式,规定:
1)x的系数为正;
2)x,y的系数及常数项一般不出现分数;
3)按含x项,含y项、常数项顺序排列.
例6 把直线l的一般式方程x-2y+6=0化为斜截式,求出直线l的斜率以及它在x轴与y轴上的截距,并画出图形.
课本例题
在直角坐标系中画直线时,通常找出直线与两点坐标轴的交点,然后连接这两个点。
拓广探索
直线
试讨论:(1) 的条件是什么?
(2) 的条件是什么?
1.根据下列条件,写出直线的方程,并把它化成一般式:
(1)经过点A(8,-2),斜率是-
(2)经过点B(4,2),平行于x轴;
(3)经过点P1(3,-2),P2(5,-4);
(4)在x轴, y轴上的截距分别是
巩固练习
答案:(1) x+2y-4=0;(2) y-2=0;(3) x+y-1=0;(4) 2x-y-3=0
2.三角形ABC的三个顶点是A(4,0), B(6,7), C(0,3),求:
(1)边BC上的中线所在直线的方程;
(2)边BC上的高所在直线的方程;
(3)边BC的垂直平分线的方程;
巩固练习
答案:(1) 5x+y-20=0;(2) 3x+2y-12=0 ;(3)3x+2y-19=0
3.已知两条直线,求: 5x+5my+6=0, : (m-2)x+15y+2m=0
(1)当m为何值时,与垂直?
(2)当m为何值时,与平行?
巩固练习
答案:(1)因为 与垂直,所以有5 (m-2) -75m=0,解得m=;
(2)因为与平行,所以有解得m=5
课堂小结
(1)直线的一般式方程:Ax+By+C=0 (A,B不同时为0)
(2)Ax+By+C=0 (A,B不同时为0)
感谢观看
