【高效备课】人教版八(上) 13.1 轴对称 13.1.2 线段的垂直平分线的性质 教案
文档属性
| 名称 | 【高效备课】人教版八(上) 13.1 轴对称 13.1.2 线段的垂直平分线的性质 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 312.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 15:09:01 | ||
图片预览

文档简介
13.1.2 线段的垂直平分线的性质
1.了解两个图形成轴对称的性质,了解轴对称图形的性质.
2.探究线段垂直平分线的性质.
3.经历探索轴对称图形性质的过程,发展空间观察能力.
4.体验数学与现实间的联系,发展审美感,激发兴趣.
【教学重点】
轴对称的性质,线段垂直平分线的性质.
【教学难点】
线段垂直平分线的性质.
一、情境导入,初步认识
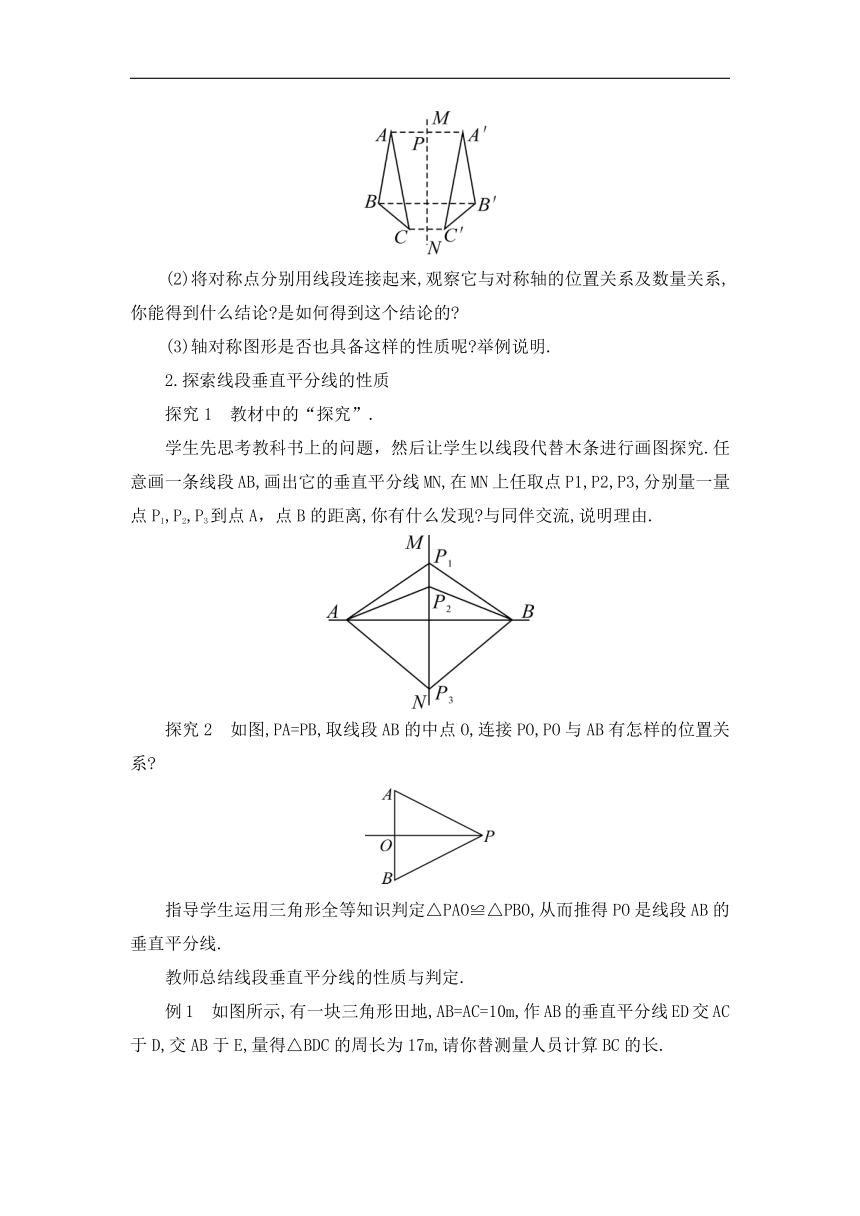
问题1 下面图形中哪些是轴对称图形 如果是,请说出它的对称轴.
问题2 如果两个图形成轴对称,那么这两个图形有什么关系
(如图2,△ABC和△A′B′C′关于直线MN对称)
【教学说明】两个图形成轴对称,那么这两个图形就全等.由此提出线段垂直平分线定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.如图3,直线l是线段AB的垂直平分线.教师讲课前,先让学生完成“自主预习”.
二、思考探究,获取新知
1.探究轴对称的性质
(1)作两个成轴对称的三角形,如图.
(2)将对称点分别用线段连接起来,观察它与对称轴的位置关系及数量关系,你能得到什么结论 是如何得到这个结论的
(3)轴对称图形是否也具备这样的性质呢 举例说明.
2.探索线段垂直平分线的性质
探究1 教材中的“探究”.
学生先思考教科书上的问题,然后让学生以线段代替木条进行画图探究.任意画一条线段AB,画出它的垂直平分线MN,在MN上任取点P1,P2,P3,分别量一量点P1,P2,P3到点A,点B的距离,你有什么发现 与同伴交流,说明理由.
探究2 如图,PA=PB,取线段AB的中点O,连接PO,PO与AB有怎样的位置关系
指导学生运用三角形全等知识判定△PAO≌△PBO,从而推得PO是线段AB的垂直平分线.
教师总结线段垂直平分线的性质与判定.
例1 如图所示,有一块三角形田地,AB=AC=10m,作AB的垂直平分线ED交AC于D,交AB于E,量得△BDC的周长为17m,请你替测量人员计算BC的长.
解:∵ED是AB的垂直平分线,
∴DA=DB.
又∵△BDC的周长为17m,AB=AC=10m,
∴BD+DC+BC=17(m).
∴DA+DC+BC=17,
即AC+BC=17(m).
∴10+BC=17(m),BC=7(m).
3.作简单轴对称图形的对称轴.
例2 如图所示,△ABC与△A′B′C′关于某条直线对称,请你作出这条直线.
【分析】△ABC与△A′B′C′中的点A与A′,点B与B′,点C与C′是对应点,连接一对对应点,如连接BB′,作线段BB′的垂直平分线即可.
解:(1)如图所示,连接BB′,分别以点B,B′为圆心,以大于BB′的长为半径作弧,两弧相交于D、E两点;
(2)作直线DE,DE即为所求的直线.
三、运用新知,深化理解
1.如果△ABC中,∠BAC=110°,P\,Q在BC上,若MP\,NQ分别垂直平分AB\,AC,则∠PAQ的度数是 .
2.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为.
3.如图所示,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6
B.5
C.4
D.3
4.如图所示,OC是∠AOB的平分线,AC⊥AO,BC⊥BO,则OC与AB的关系是( ).
A.AB垂直平分OC
B.OC垂直平分AB
C.OC只平分AB但不垂直
D.OC只垂直AB但不平分
5.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
【教学说明】指导学生解答上述习题时,强调学生应:(1)注意成轴对称的两个图形的全等关系,由此可得到几组边、角的相等;(2)注意线段垂直平分线的性质的灵活运用.
【答案】1.40° 2.8cm2 3.B 4.B
5.(1)∵DE垂直平分AC,∴CE=AE,∴∠ECD=∠A=36°.(2)∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,∵∠ECD=36°,∴∠BCE=∠ACB-∠ECD=36°,∴∠BEC=72°=∠B,∴BC=EC=5.
四、师生互动,课堂小结
问题:本节课学会了什么 有哪些收获 还有什么疑问
由学生表述,教师归纳总结.
1.布置作业:从教材“习题13.1”中选取.
2.完成练习册中本课时的练习.
本课教学力求充分体现内容的基础性,方法的灵活性、学生学习的主体性和教学的主导性,在学习活动中,要求学生主动参与,认真思考、比较观察、动手交流和表述,并借助多媒体的手段辅助教学,增强直观性、激发学习兴趣.
强调分组讨论,学生与学生之间很好地交流与合作,利用师生的双边活动,激发学生学习兴趣,教师从中发现、搜集学生的学习情况,查漏补缺,适时调度,从而顺利达到教学的目的.
1.了解两个图形成轴对称的性质,了解轴对称图形的性质.
2.探究线段垂直平分线的性质.
3.经历探索轴对称图形性质的过程,发展空间观察能力.
4.体验数学与现实间的联系,发展审美感,激发兴趣.
【教学重点】
轴对称的性质,线段垂直平分线的性质.
【教学难点】
线段垂直平分线的性质.
一、情境导入,初步认识
问题1 下面图形中哪些是轴对称图形 如果是,请说出它的对称轴.
问题2 如果两个图形成轴对称,那么这两个图形有什么关系
(如图2,△ABC和△A′B′C′关于直线MN对称)
【教学说明】两个图形成轴对称,那么这两个图形就全等.由此提出线段垂直平分线定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.如图3,直线l是线段AB的垂直平分线.教师讲课前,先让学生完成“自主预习”.
二、思考探究,获取新知
1.探究轴对称的性质
(1)作两个成轴对称的三角形,如图.
(2)将对称点分别用线段连接起来,观察它与对称轴的位置关系及数量关系,你能得到什么结论 是如何得到这个结论的
(3)轴对称图形是否也具备这样的性质呢 举例说明.
2.探索线段垂直平分线的性质
探究1 教材中的“探究”.
学生先思考教科书上的问题,然后让学生以线段代替木条进行画图探究.任意画一条线段AB,画出它的垂直平分线MN,在MN上任取点P1,P2,P3,分别量一量点P1,P2,P3到点A,点B的距离,你有什么发现 与同伴交流,说明理由.
探究2 如图,PA=PB,取线段AB的中点O,连接PO,PO与AB有怎样的位置关系
指导学生运用三角形全等知识判定△PAO≌△PBO,从而推得PO是线段AB的垂直平分线.
教师总结线段垂直平分线的性质与判定.
例1 如图所示,有一块三角形田地,AB=AC=10m,作AB的垂直平分线ED交AC于D,交AB于E,量得△BDC的周长为17m,请你替测量人员计算BC的长.
解:∵ED是AB的垂直平分线,
∴DA=DB.
又∵△BDC的周长为17m,AB=AC=10m,
∴BD+DC+BC=17(m).
∴DA+DC+BC=17,
即AC+BC=17(m).
∴10+BC=17(m),BC=7(m).
3.作简单轴对称图形的对称轴.
例2 如图所示,△ABC与△A′B′C′关于某条直线对称,请你作出这条直线.
【分析】△ABC与△A′B′C′中的点A与A′,点B与B′,点C与C′是对应点,连接一对对应点,如连接BB′,作线段BB′的垂直平分线即可.
解:(1)如图所示,连接BB′,分别以点B,B′为圆心,以大于BB′的长为半径作弧,两弧相交于D、E两点;
(2)作直线DE,DE即为所求的直线.
三、运用新知,深化理解
1.如果△ABC中,∠BAC=110°,P\,Q在BC上,若MP\,NQ分别垂直平分AB\,AC,则∠PAQ的度数是 .
2.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为.
3.如图所示,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6
B.5
C.4
D.3
4.如图所示,OC是∠AOB的平分线,AC⊥AO,BC⊥BO,则OC与AB的关系是( ).
A.AB垂直平分OC
B.OC垂直平分AB
C.OC只平分AB但不垂直
D.OC只垂直AB但不平分
5.如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC的长.
【教学说明】指导学生解答上述习题时,强调学生应:(1)注意成轴对称的两个图形的全等关系,由此可得到几组边、角的相等;(2)注意线段垂直平分线的性质的灵活运用.
【答案】1.40° 2.8cm2 3.B 4.B
5.(1)∵DE垂直平分AC,∴CE=AE,∴∠ECD=∠A=36°.(2)∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,∵∠ECD=36°,∴∠BCE=∠ACB-∠ECD=36°,∴∠BEC=72°=∠B,∴BC=EC=5.
四、师生互动,课堂小结
问题:本节课学会了什么 有哪些收获 还有什么疑问
由学生表述,教师归纳总结.
1.布置作业:从教材“习题13.1”中选取.
2.完成练习册中本课时的练习.
本课教学力求充分体现内容的基础性,方法的灵活性、学生学习的主体性和教学的主导性,在学习活动中,要求学生主动参与,认真思考、比较观察、动手交流和表述,并借助多媒体的手段辅助教学,增强直观性、激发学习兴趣.
强调分组讨论,学生与学生之间很好地交流与合作,利用师生的双边活动,激发学生学习兴趣,教师从中发现、搜集学生的学习情况,查漏补缺,适时调度,从而顺利达到教学的目的.
