【高效备课】人教版八(上) 第13章 轴对称 章末复习 教案
文档属性
| 名称 | 【高效备课】人教版八(上) 第13章 轴对称 章末复习 教案 | 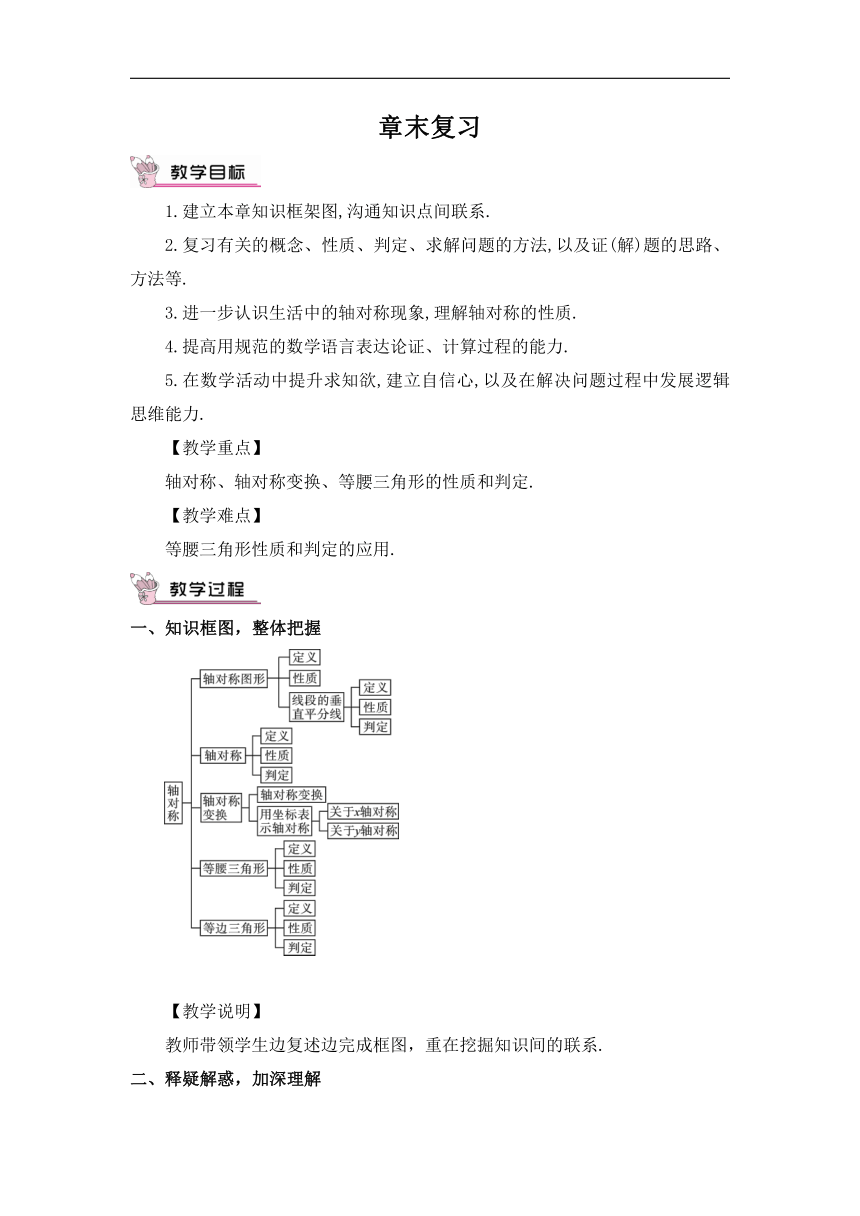 | |
| 格式 | doc | ||
| 文件大小 | 797.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 15:09:01 | ||
图片预览


文档简介
章末复习
1.建立本章知识框架图,沟通知识点间联系.
2.复习有关的概念、性质、判定、求解问题的方法,以及证(解)题的思路、方法等.
3.进一步认识生活中的轴对称现象,理解轴对称的性质.
4.提高用规范的数学语言表达论证、计算过程的能力.
5.在数学活动中提升求知欲,建立自信心,以及在解决问题过程中发展逻辑思维能力.
【教学重点】
轴对称、轴对称变换、等腰三角形的性质和判定.
【教学难点】
等腰三角形性质和判定的应用.
一、知识框图,整体把握
【教学说明】
教师带领学生边复述边完成框图,重在挖掘知识间的联系.
二、释疑解惑,加深理解
本章知识体现了数学思想,教师归纳讲解,帮助学生提升能力.
1.数形结合思想在坐标系中的应用
用坐标表示轴对称,体现了数与形的结合,直观,易于理解与认识.
例1 求P(3,2)关于x轴、关于直线x=-1对称点的坐标.
解:分别为P′(3,-2),P″(-5,2).
【教学说明】根据题中要求和对称特点,画出相应示意图,结果就一目了然.
2.分类讨论思想解决等腰三角形问题
例2 若等腰三角形的一个角为50°,求顶角的度数.
【分析】50°的角可能是等腰三角形的顶角,也可能是底角.
解:当底角为50°时,顶角为80°,故等腰三角形的顶角为50°或80°.
【教学说明】
由于等腰三角形的特殊性,做题时要注意分类思想的应用,要看已知角是顶角还是底角,已知边是腰还是底边,腰上的高是在三角形的内部还是在外部,考虑周全才不致于漏解.
3.利用方程思想求值
例3 等腰三角形的周长为30cm,一边长是12cm,求另两边的长.
【分析】本题已知长为12cm的边,不确定是腰或底边,所以要分两种情况求解.
解:当腰长为12cm时,设底边长为xcm,
∵x+2×12=30,
∴x=6.
当底边长为12cm时,设腰长为ycm.
∵2y+12=30,
∴y=9.
因此,三角形另两边的长为12cm,6cm或9cm,9cm.
【教学说明】用方程思想解几何题是常用的思路和方法.
三、典例精析,复习新知
例4 如图,凸四边形ABCD的对角线AC,BD相交于点O,且AC⊥BD.已知OA>OC,OB>OD,试比较BC+AD与AB+CD的大小.
【分析】利用轴对称变换,以及三角形两边之和大于第三边,能很直观地得出BC+AD>AB+CD的结论.
解:如图,以AC为对称轴,将△ADO翻折,由于AC⊥BD,则点D必落在BO上,设为D′,
则AD′=AD,OD′=OD.
同理,将△BCO翻折,点C必落在AO上,设为C′,则BC′=BC,OC′=OC.
连C′D′,BC′,AD′,CD′,设BC′与AD′交于点E,
则C′D′=CD.
在△ABE和△C′D′E′中,
C′E+D′E>C′D′,①
BE+AE>AB.②
①+②得BC′+AD′>AB+C′D′,即BC+AD>AB+CD.
【教学说明】利用轴对称变换可得出边、角相等的一系列结论,所以要求学生能够灵活地应用这种变换.
例5 如图,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.试探究线段CN、BM、MN之间的关系,并加以证明.
【分析】通过观察可以猜想这三条线段之间的关系为MN=CN+BM.通过观察可以猜想这三条线段之间的关系为MN=CN+BM.这类问题的证明方法通常是将MN截成两段,或将NC或MB延长,补成长为CN+BM的线段,运用全等三角形论证.
解:BM+CN=MN.
证明:如图,延长AC至M1,使CM1=BM,连接DM1.
∵△ABC是正三角形,∴∠ABC=∠ACB=60°.
∵∠BDC=120°,且BD=CD,
∴∠DBC=∠DCB=30°.
∴∠ABD=∠ACD=90°.∠DCM1=90°.
又∵BD=CD,BM=CM1,
∴Rt△BDM≌Rt△CDM1(SAS).
∴DM=DM1,∠BDM=∠CDM1,
∴∠MDM1=∠MDC+CDM1=∠MDC+∠BDM=∠BDC=120°.
又∵∠MDN=60°,
∴∠M1DN=∠MDN=60°.
又∵DM=DM1,DN=DN,
∴△MDN≌△M1DN(SAS).
∴MN=M1N=NC+M1C=CN+BM.
【教学说明】
对于此类题,三条线段之间的关系一般是它们的和差关系,证明方法通常采用截长补短法.
例6 如图,花边中的图案以正方形为基础,由圆弧或圆构成,依照例图,请你为班级黑板报设计一条花边.
要求:只要画出组成花边的一个图案,不写画法,不需要文字;以所给的正方形为基础,用圆弧或圆画出;图案应有美感;与例图不同.
【分析】本题主要考查大家根据轴对称性质设计花边图案的能力,而且要符合题中的四点要求,这是一道融数学与美术为一体的综合创新素质题.
【答案】此题答案不唯一,略举几例如图所示.
【教学说明】数学知识与现实生活紧密相连,眼前轴对称的应用比比皆是,提醒每个学生留心,从生活实际中提升对轴对称的认识.
1.布置作业:从教材“复习题13”中选取.
2.完成练习册中本课时的练习.
本章知识与现实生活联系密切,是人们日常生活和生产中应用较广的几何图形,是三角形知识的延续与拓展,涉及的轴对称、线段垂直平分线、等腰三角形知识,可让解题从全等的模式中解脱出来,而且可简便解决相关的计算、证明问题,使解题过程简化,在复习中应强化这些知识.
1.建立本章知识框架图,沟通知识点间联系.
2.复习有关的概念、性质、判定、求解问题的方法,以及证(解)题的思路、方法等.
3.进一步认识生活中的轴对称现象,理解轴对称的性质.
4.提高用规范的数学语言表达论证、计算过程的能力.
5.在数学活动中提升求知欲,建立自信心,以及在解决问题过程中发展逻辑思维能力.
【教学重点】
轴对称、轴对称变换、等腰三角形的性质和判定.
【教学难点】
等腰三角形性质和判定的应用.
一、知识框图,整体把握
【教学说明】
教师带领学生边复述边完成框图,重在挖掘知识间的联系.
二、释疑解惑,加深理解
本章知识体现了数学思想,教师归纳讲解,帮助学生提升能力.
1.数形结合思想在坐标系中的应用
用坐标表示轴对称,体现了数与形的结合,直观,易于理解与认识.
例1 求P(3,2)关于x轴、关于直线x=-1对称点的坐标.
解:分别为P′(3,-2),P″(-5,2).
【教学说明】根据题中要求和对称特点,画出相应示意图,结果就一目了然.
2.分类讨论思想解决等腰三角形问题
例2 若等腰三角形的一个角为50°,求顶角的度数.
【分析】50°的角可能是等腰三角形的顶角,也可能是底角.
解:当底角为50°时,顶角为80°,故等腰三角形的顶角为50°或80°.
【教学说明】
由于等腰三角形的特殊性,做题时要注意分类思想的应用,要看已知角是顶角还是底角,已知边是腰还是底边,腰上的高是在三角形的内部还是在外部,考虑周全才不致于漏解.
3.利用方程思想求值
例3 等腰三角形的周长为30cm,一边长是12cm,求另两边的长.
【分析】本题已知长为12cm的边,不确定是腰或底边,所以要分两种情况求解.
解:当腰长为12cm时,设底边长为xcm,
∵x+2×12=30,
∴x=6.
当底边长为12cm时,设腰长为ycm.
∵2y+12=30,
∴y=9.
因此,三角形另两边的长为12cm,6cm或9cm,9cm.
【教学说明】用方程思想解几何题是常用的思路和方法.
三、典例精析,复习新知
例4 如图,凸四边形ABCD的对角线AC,BD相交于点O,且AC⊥BD.已知OA>OC,OB>OD,试比较BC+AD与AB+CD的大小.
【分析】利用轴对称变换,以及三角形两边之和大于第三边,能很直观地得出BC+AD>AB+CD的结论.
解:如图,以AC为对称轴,将△ADO翻折,由于AC⊥BD,则点D必落在BO上,设为D′,
则AD′=AD,OD′=OD.
同理,将△BCO翻折,点C必落在AO上,设为C′,则BC′=BC,OC′=OC.
连C′D′,BC′,AD′,CD′,设BC′与AD′交于点E,
则C′D′=CD.
在△ABE和△C′D′E′中,
C′E+D′E>C′D′,①
BE+AE>AB.②
①+②得BC′+AD′>AB+C′D′,即BC+AD>AB+CD.
【教学说明】利用轴对称变换可得出边、角相等的一系列结论,所以要求学生能够灵活地应用这种变换.
例5 如图,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.试探究线段CN、BM、MN之间的关系,并加以证明.
【分析】通过观察可以猜想这三条线段之间的关系为MN=CN+BM.通过观察可以猜想这三条线段之间的关系为MN=CN+BM.这类问题的证明方法通常是将MN截成两段,或将NC或MB延长,补成长为CN+BM的线段,运用全等三角形论证.
解:BM+CN=MN.
证明:如图,延长AC至M1,使CM1=BM,连接DM1.
∵△ABC是正三角形,∴∠ABC=∠ACB=60°.
∵∠BDC=120°,且BD=CD,
∴∠DBC=∠DCB=30°.
∴∠ABD=∠ACD=90°.∠DCM1=90°.
又∵BD=CD,BM=CM1,
∴Rt△BDM≌Rt△CDM1(SAS).
∴DM=DM1,∠BDM=∠CDM1,
∴∠MDM1=∠MDC+CDM1=∠MDC+∠BDM=∠BDC=120°.
又∵∠MDN=60°,
∴∠M1DN=∠MDN=60°.
又∵DM=DM1,DN=DN,
∴△MDN≌△M1DN(SAS).
∴MN=M1N=NC+M1C=CN+BM.
【教学说明】
对于此类题,三条线段之间的关系一般是它们的和差关系,证明方法通常采用截长补短法.
例6 如图,花边中的图案以正方形为基础,由圆弧或圆构成,依照例图,请你为班级黑板报设计一条花边.
要求:只要画出组成花边的一个图案,不写画法,不需要文字;以所给的正方形为基础,用圆弧或圆画出;图案应有美感;与例图不同.
【分析】本题主要考查大家根据轴对称性质设计花边图案的能力,而且要符合题中的四点要求,这是一道融数学与美术为一体的综合创新素质题.
【答案】此题答案不唯一,略举几例如图所示.
【教学说明】数学知识与现实生活紧密相连,眼前轴对称的应用比比皆是,提醒每个学生留心,从生活实际中提升对轴对称的认识.
1.布置作业:从教材“复习题13”中选取.
2.完成练习册中本课时的练习.
本章知识与现实生活联系密切,是人们日常生活和生产中应用较广的几何图形,是三角形知识的延续与拓展,涉及的轴对称、线段垂直平分线、等腰三角形知识,可让解题从全等的模式中解脱出来,而且可简便解决相关的计算、证明问题,使解题过程简化,在复习中应强化这些知识.
