【高效备课】人教版八(上) 第15章 分式 章末复习 教案
文档属性
| 名称 | 【高效备课】人教版八(上) 第15章 分式 章末复习 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 400.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 15:09:01 | ||
图片预览


文档简介
章末复习
1.进一步了解本章学过的主要知识,能用它们解决具体问题;
2.进一步增强分式的混合运算能力,解分式方程的能力,能根据实际问题构建分式方程并解决应用问题的能力.
3.经历“知识结构图——问题反思——实际应用”的探索过程,增强学生的数学类比思想、化归思想的意识,增强分析问题、解决问题的能力.
4.在学生的相互交流、共同探究的问题过程中,进一步增强学生的合作交流意识和探究精神,培养良好的学习习惯,增强求知欲望.
【教学重点】
1.分式的基本概念;
2.分式的有(无)意义;
3.分式的基本性质;
4.分式的化简与计算;
5.负整数指数幂与科学记数法;
6.解分式方程;
7.分式方程的应用.
【教学难点】
1.分式的化简求值;
2.分式的混合运算;
3.分式方程增根的理解;
4.分式方程的实际运用.
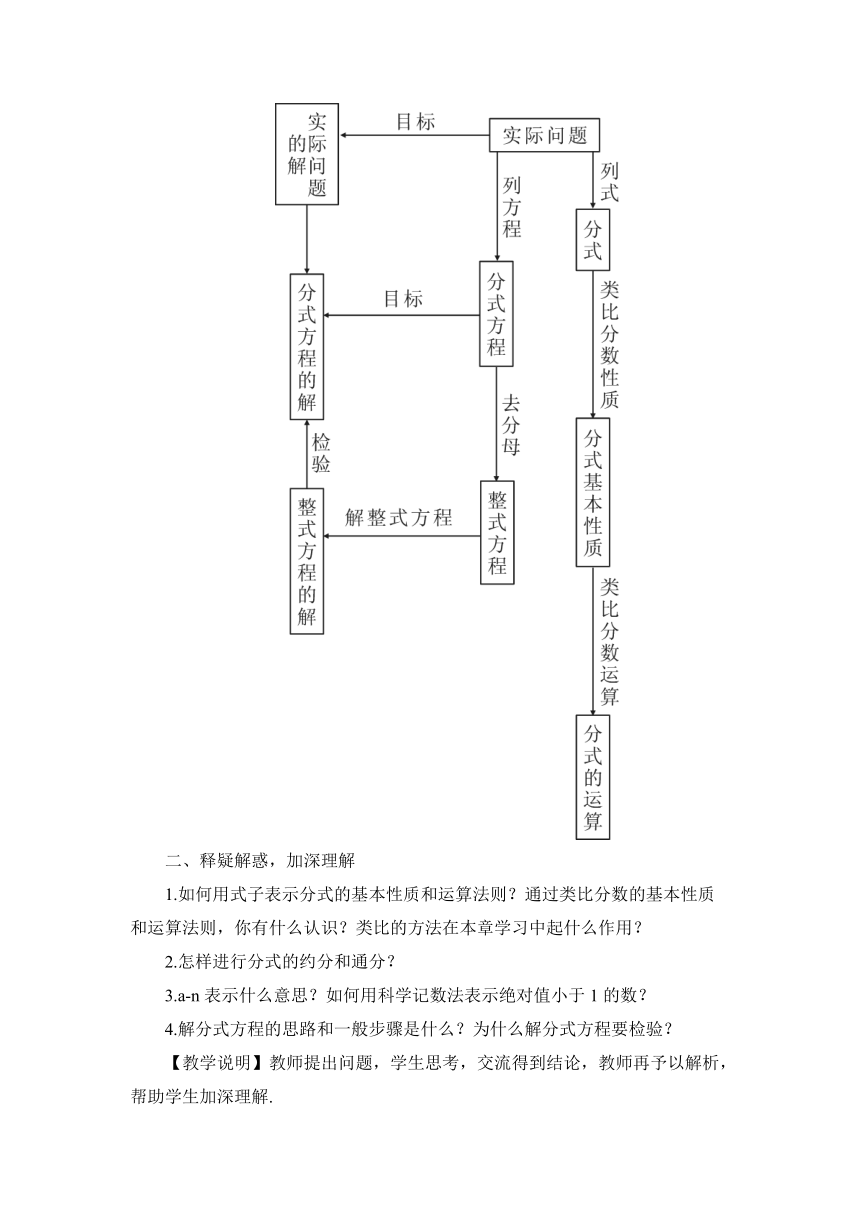
一、知识框图,整体把握
【教学说明】下面结构图的构建是在教师与学生一道回顾本章知识过程中,边回顾边构建,通过结构图可让学生系统地回顾本章主要知识.
本章知识结构图
二、释疑解惑,加深理解
1.如何用式子表示分式的基本性质和运算法则?通过类比分数的基本性质和运算法则,你有什么认识?类比的方法在本章学习中起什么作用?
2.怎样进行分式的约分和通分?
3.a-n表示什么意思?如何用科学记数法表示绝对值小于1的数?
4.解分式方程的思路和一般步骤是什么?为什么解分式方程要检验?
【教学说明】教师提出问题,学生思考,交流得到结论,教师再予以解析,帮助学生加深理解.
三、典例精析,复习新知
例1(1)关于甲醛污染问题一直困扰人们.我国质检总局规定:针织内衣、被套、床上用品等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下,将0.000075用科学记数法表示为( )
A.0.75×10-4 B.7.5×10-4
C.7.5×10-5 D.75×10-6
(2)若分式的值为0,则x的值等于 .
(3)化简 = .
(4)某玩具厂生产一种玩具,甲车间计划生产500个,乙车间计划生产400个,甲车间每天比乙车间多生产10个,两车间同时开始生产且同时完成任务.设乙车间每天生产x个,可列方程为( )
【教学说明】这里的四道小题可由学生自己给出答案,教师展示答案供学生自查即可.
【答案】(1)C(2)x=1(3)a-1(4)B
例2分式方程 有增根,则m的值为( )
A.0和3 B.1 C.1和-2 D.3
【分析】将分式方程化为整式方程为x(x+2)-(x-1)(x+2)=m,整理得x=m-2,要使原分式方程有增根,则应有(x-1)(x+2)=0,∴x=1或x=-2.∴m-2=1或m-2=-2,解得m=3或m=0.当m=0时,原分式方程为 ,此方程可化为x=x-1,而0≠-1,原分式方程无解,且没有增根,应舍去,而当m=3时,原分式方程无解,但有增根x=1,故选D.
【教学说明】本章在实际教学时可根据需要取舍,若选用,则应由教师予以评讲.
例3(1)先化简,再求值: ,其中a为整数,且-3(2)化简求值: ,从0,1,2三个数中选取一个合适的数值作为x值代入求值.
【分析】(1)中化简结果为a++a,又∵a+2≠0,(a+1)(a-1)≠0,∴a≠-2,a≠-1,且a≠1,又a为整数且-3(2)中化简结果为,又∵x-1≠0,x≠0,∴x≠1且x≠0,故x的值只有选取2,即x=2,故原式的值为 .
【教学说明】上述两题的关键在于选取恰当的a值或x值代入求值,而要求选取的值必须保证原来分式有意义才行,应引起学生注意,切不可大意出错.
【教学说明】本例有3小题,教师可选取一题讲题,剩下两题让学生试着自己探索.本例的3个小题需要注意的是:(1)题将已知条件变换成适合化简所需形式,从而达到整体代入化简求值的目的;(2)题要注意完全平方公式的灵活运用;(3)题完全平方公式(a+b)2=a2+2ab+b2变形为a2+b2=(a+b)2-2ab,此类题运用公式和互为倒数的两数之积为1的特点,进行变形求值.
例5(1)某文化用品商店用2000元购进一批学生书包,上市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
①求第一批购进书包的单价是多少元?
②若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共赢利多少元?
(2)某开发商要建一批住房,经调查了解,若甲、乙两队分别单独完成,则乙队完成的天数是甲队的1.5倍;若甲、乙两队合作,则需120天完成.
①甲、乙两边单独完成各需多少天?
②施工过程中,开发商派2名工程师全程监督,需支付每人每天食宿费150元.已知乙队单独施工,开发商每天需支付施工费为10000元.现从甲、乙两队中选一队单独施工,若要使开发商选甲队支付的总费用不超过选乙队的,则甲队每天的施工费最多为多少元?
【分析】(1)①设第一批购进书包的单价为x元,可列方程为 ,得x=80,经检验,x=80是原分式方程的解,可知第一批书包单价为80元;
②易知第一批购进25个,则第二批进了75个,可得商店两次共赢利3700元;
(2)设甲队单独完成需x天,则有 ,解得x=200.
经检验知x=200是原分式方程的解,故乙队单独完成需300天;
②乙队所需总费用为(10000+2×150)×300=3090000元,说甲队每天的施工费为y元,则有(y+2×150)×200≤3090000,将y≤15150,即甲队每天施工费最多为15150元.
【教学说明】例5中两题实际教学过程中只需选取1题即可,先由学生独立思考试试,然后予以评讲.
四、师生互动,课堂小结
这节课你有哪些收获?你觉得还有哪些地方存在疑问,不妨与同伴交流.
【教学说明】教师提出问题,让学生在相互交流中加深理解,感受合作学习的乐趣,完善认知.
1.布置作业:从教材“复习题15”中选取.
2.完成练习册中本课时的练习.
本课是全章的复习课.考虑到实际问题,本章复习的教学主要采取以例题讲解和知识回顾相结合的方法进行.对于本章教学的难点如分式的四则混合运算、根据实际问题列方程等,老师要着重讲解.分式是不同于整式的另一类有理式,是代数式中重要的基本概念,相应地,分式方程是一类有理方程,解分式方程的过程比解整式方程更复杂些.然而,分式或分式方程更适合作为某些类型问题的数学模型,它们具有整式或整式方程不可替代的作用.解分式方程时,化归思想很有用,分式方程都要先化为整式方程再求解,并且要注意检验是必不可少的步骤.
因此,老师在引导学生进行复习时,要使学生系统地掌握分式的化简、求值和混合运算以及运用分式方程解决实际问题等相关知识.
此外,教学过程中,教师应更多地让学生积极参与课堂,多动手、多动脑、多交流,让学生体会学习的乐趣.
1.进一步了解本章学过的主要知识,能用它们解决具体问题;
2.进一步增强分式的混合运算能力,解分式方程的能力,能根据实际问题构建分式方程并解决应用问题的能力.
3.经历“知识结构图——问题反思——实际应用”的探索过程,增强学生的数学类比思想、化归思想的意识,增强分析问题、解决问题的能力.
4.在学生的相互交流、共同探究的问题过程中,进一步增强学生的合作交流意识和探究精神,培养良好的学习习惯,增强求知欲望.
【教学重点】
1.分式的基本概念;
2.分式的有(无)意义;
3.分式的基本性质;
4.分式的化简与计算;
5.负整数指数幂与科学记数法;
6.解分式方程;
7.分式方程的应用.
【教学难点】
1.分式的化简求值;
2.分式的混合运算;
3.分式方程增根的理解;
4.分式方程的实际运用.
一、知识框图,整体把握
【教学说明】下面结构图的构建是在教师与学生一道回顾本章知识过程中,边回顾边构建,通过结构图可让学生系统地回顾本章主要知识.
本章知识结构图
二、释疑解惑,加深理解
1.如何用式子表示分式的基本性质和运算法则?通过类比分数的基本性质和运算法则,你有什么认识?类比的方法在本章学习中起什么作用?
2.怎样进行分式的约分和通分?
3.a-n表示什么意思?如何用科学记数法表示绝对值小于1的数?
4.解分式方程的思路和一般步骤是什么?为什么解分式方程要检验?
【教学说明】教师提出问题,学生思考,交流得到结论,教师再予以解析,帮助学生加深理解.
三、典例精析,复习新知
例1(1)关于甲醛污染问题一直困扰人们.我国质检总局规定:针织内衣、被套、床上用品等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下,将0.000075用科学记数法表示为( )
A.0.75×10-4 B.7.5×10-4
C.7.5×10-5 D.75×10-6
(2)若分式的值为0,则x的值等于 .
(3)化简 = .
(4)某玩具厂生产一种玩具,甲车间计划生产500个,乙车间计划生产400个,甲车间每天比乙车间多生产10个,两车间同时开始生产且同时完成任务.设乙车间每天生产x个,可列方程为( )
【教学说明】这里的四道小题可由学生自己给出答案,教师展示答案供学生自查即可.
【答案】(1)C(2)x=1(3)a-1(4)B
例2分式方程 有增根,则m的值为( )
A.0和3 B.1 C.1和-2 D.3
【分析】将分式方程化为整式方程为x(x+2)-(x-1)(x+2)=m,整理得x=m-2,要使原分式方程有增根,则应有(x-1)(x+2)=0,∴x=1或x=-2.∴m-2=1或m-2=-2,解得m=3或m=0.当m=0时,原分式方程为 ,此方程可化为x=x-1,而0≠-1,原分式方程无解,且没有增根,应舍去,而当m=3时,原分式方程无解,但有增根x=1,故选D.
【教学说明】本章在实际教学时可根据需要取舍,若选用,则应由教师予以评讲.
例3(1)先化简,再求值: ,其中a为整数,且-3
【分析】(1)中化简结果为a++a,又∵a+2≠0,(a+1)(a-1)≠0,∴a≠-2,a≠-1,且a≠1,又a为整数且-3
【教学说明】上述两题的关键在于选取恰当的a值或x值代入求值,而要求选取的值必须保证原来分式有意义才行,应引起学生注意,切不可大意出错.
【教学说明】本例有3小题,教师可选取一题讲题,剩下两题让学生试着自己探索.本例的3个小题需要注意的是:(1)题将已知条件变换成适合化简所需形式,从而达到整体代入化简求值的目的;(2)题要注意完全平方公式的灵活运用;(3)题完全平方公式(a+b)2=a2+2ab+b2变形为a2+b2=(a+b)2-2ab,此类题运用公式和互为倒数的两数之积为1的特点,进行变形求值.
例5(1)某文化用品商店用2000元购进一批学生书包,上市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
①求第一批购进书包的单价是多少元?
②若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共赢利多少元?
(2)某开发商要建一批住房,经调查了解,若甲、乙两队分别单独完成,则乙队完成的天数是甲队的1.5倍;若甲、乙两队合作,则需120天完成.
①甲、乙两边单独完成各需多少天?
②施工过程中,开发商派2名工程师全程监督,需支付每人每天食宿费150元.已知乙队单独施工,开发商每天需支付施工费为10000元.现从甲、乙两队中选一队单独施工,若要使开发商选甲队支付的总费用不超过选乙队的,则甲队每天的施工费最多为多少元?
【分析】(1)①设第一批购进书包的单价为x元,可列方程为 ,得x=80,经检验,x=80是原分式方程的解,可知第一批书包单价为80元;
②易知第一批购进25个,则第二批进了75个,可得商店两次共赢利3700元;
(2)设甲队单独完成需x天,则有 ,解得x=200.
经检验知x=200是原分式方程的解,故乙队单独完成需300天;
②乙队所需总费用为(10000+2×150)×300=3090000元,说甲队每天的施工费为y元,则有(y+2×150)×200≤3090000,将y≤15150,即甲队每天施工费最多为15150元.
【教学说明】例5中两题实际教学过程中只需选取1题即可,先由学生独立思考试试,然后予以评讲.
四、师生互动,课堂小结
这节课你有哪些收获?你觉得还有哪些地方存在疑问,不妨与同伴交流.
【教学说明】教师提出问题,让学生在相互交流中加深理解,感受合作学习的乐趣,完善认知.
1.布置作业:从教材“复习题15”中选取.
2.完成练习册中本课时的练习.
本课是全章的复习课.考虑到实际问题,本章复习的教学主要采取以例题讲解和知识回顾相结合的方法进行.对于本章教学的难点如分式的四则混合运算、根据实际问题列方程等,老师要着重讲解.分式是不同于整式的另一类有理式,是代数式中重要的基本概念,相应地,分式方程是一类有理方程,解分式方程的过程比解整式方程更复杂些.然而,分式或分式方程更适合作为某些类型问题的数学模型,它们具有整式或整式方程不可替代的作用.解分式方程时,化归思想很有用,分式方程都要先化为整式方程再求解,并且要注意检验是必不可少的步骤.
因此,老师在引导学生进行复习时,要使学生系统地掌握分式的化简、求值和混合运算以及运用分式方程解决实际问题等相关知识.
此外,教学过程中,教师应更多地让学生积极参与课堂,多动手、多动脑、多交流,让学生体会学习的乐趣.
