2023-2024学年北师大版数学八年级上册 2.1 认识无理数 课件(共20张PPT)
文档属性
| 名称 | 2023-2024学年北师大版数学八年级上册 2.1 认识无理数 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 497.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
2.1认识无理数
教学目标
1.通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性。
2.能判断给出的数是否为有理数;并能说出理由。
1.让学生亲自动手做拼图活动,感受无理数存在的必要性和合理性,培养大家的动手能力和合作精神。
2.通过回顾有理数的有关知识,能正确地进行推理和判断,识别某些数是否为有理数,训练他们的思维判断能力。
1.激励学生积极参与教学活动,提高大家学习数学的热情。2.引导学生充分进行交流,讨论与探索等教学活动,培养他们的合作与钻研精神。
3.了解有关无理数发现的知识,鼓励学生大胆质疑,追求真理。
教学重难点
1.让学生经历无理数发现的过程.感知生活中确实存在着不同于有理数的数。2.会判断一个数是否为有理数。
1.把两个边长为1的正方形拼成一个大正方形的动手操作过程。2.判断一个数是否为有理数。
约公元前500年的希腊,毕达哥拉斯是当时希腊学术界的权威,辉煌的毕达哥拉斯学派的掌门人。毕氏开创的学术信条是“万物皆数”,即任何事物都可以用整数或者两个整数之比来表示。可惜好景不长,学派的小弟子希伯索斯“偶然间”发现了一个惊人的事实,为了保持学派的地位和真理的尊严,毕氏决定封锁消息,追杀叛徒。最后可怜的希伯索斯被无情的抛入大海,数学的又一巨大进步就这样拉开了序幕!
情景引入
温故新知
1.我们学过的数有哪些?
小学学过自然描数、小数、分数,进入初中又学习了负数
2.什么叫做有理数
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如 , , 5.2, …
负分数:如 , ,-3.5, …
有理数
1.什么叫有理数?
除了有理数外还有没有其它的数呢?
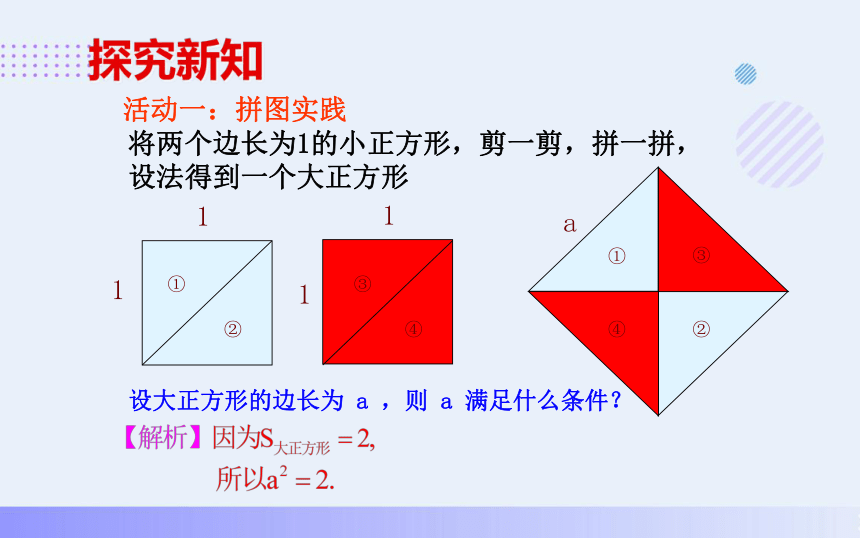
活动一:拼图实践
将两个边长为1的小正方形,剪一剪,拼一拼,
设法得到一个大正方形
1
1
1
1
①
②
③
④
①
②
③
④
设大正方形的边长为 a ,则 a 满足什么条件?
a
探究新知
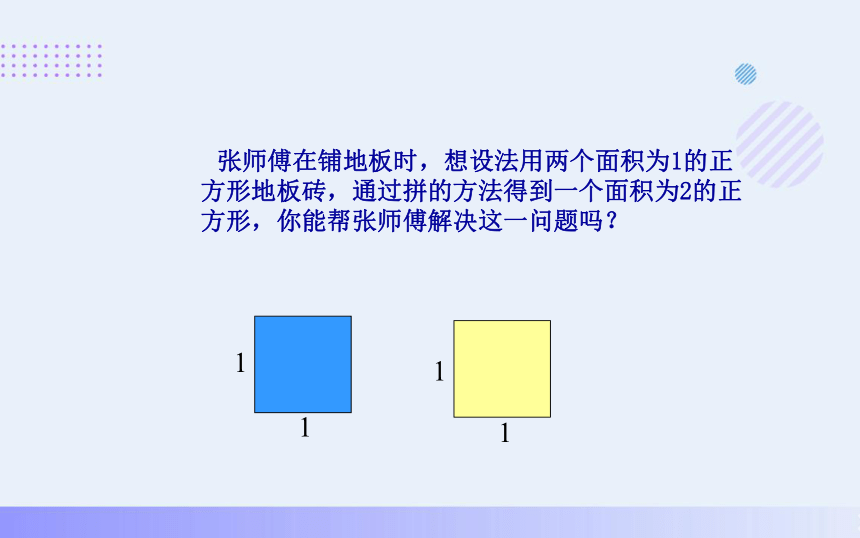
张师傅在铺地板时,想设法用两个面积为1的正方形地板砖,通过拼的方法得到一个面积为2的正方形,你能帮张师傅解决这一问题吗?
1
1
1
1
1
1
1
1
思考:无论以什么样的方式拼接,你所得到的大正方形的面积是多少?
1
1
1
1
1
1
1
1
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
问题1 设大正方形的边长为a,则a满足什么条件?
∵ S大正方形=2,∴ a2=2。
探究问题一:无理数的存在性
问题2:a是一个什么样的数?a可能是整数吗?
从“数”的角度:
∵ a2=2, 而12=1, 22=4 ,
∴ 12∴ 1< a< 2,a不是整数。
探究问题一:无理数的存在性
从“形”的角度:
取出一个三角形
∵在三角形ABC中,AC=1,AB=1,BC=a;
根据三角形的三边关系:
AC-AB< a∴0探究问题一:无理数的存在性
问题3:a可能是分数吗?
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
探究问题一:无理数的存在性
问题3:a可能是分数吗?
问题4:根据问题2、3的结果, 你得到什么结论?
归纳:a既不是整数,也不是分数,所以a不是有理数。
探究问题一:无理数的存在性
问题2:a是一个什么样的数?a可能是整数吗?
质疑问题 a 究竟是多少?
1
面积为2
a
2
a的整数部分是几?十分位是几?百分位呢?
探究问题二:估算无理数的近似值
1、小组内讨论如何确定a的个位数、十分位、百分位、千分位的大小,总结方法;
2、组长带领组员交流讨论在预习过程中遇到的问题并订正导案中的内容;
3、把未解决问题贴到黑板上;
交流讨论
下列数哪些是有理数 哪些是无理数
3.14159,
-5.232 332…,
123.345 678 910 11…(由相继的正整数组成).
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( )
判断题
╳
√
√
╳
右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.试分别找出两条长度是有理数的线段和两条长度是无理数的线段.
1、无理数的存在性
2、估计无理数的近似值
无限逼近法
3、数的分类
小结
2.1认识无理数
教学目标
1.通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性。
2.能判断给出的数是否为有理数;并能说出理由。
1.让学生亲自动手做拼图活动,感受无理数存在的必要性和合理性,培养大家的动手能力和合作精神。
2.通过回顾有理数的有关知识,能正确地进行推理和判断,识别某些数是否为有理数,训练他们的思维判断能力。
1.激励学生积极参与教学活动,提高大家学习数学的热情。2.引导学生充分进行交流,讨论与探索等教学活动,培养他们的合作与钻研精神。
3.了解有关无理数发现的知识,鼓励学生大胆质疑,追求真理。
教学重难点
1.让学生经历无理数发现的过程.感知生活中确实存在着不同于有理数的数。2.会判断一个数是否为有理数。
1.把两个边长为1的正方形拼成一个大正方形的动手操作过程。2.判断一个数是否为有理数。
约公元前500年的希腊,毕达哥拉斯是当时希腊学术界的权威,辉煌的毕达哥拉斯学派的掌门人。毕氏开创的学术信条是“万物皆数”,即任何事物都可以用整数或者两个整数之比来表示。可惜好景不长,学派的小弟子希伯索斯“偶然间”发现了一个惊人的事实,为了保持学派的地位和真理的尊严,毕氏决定封锁消息,追杀叛徒。最后可怜的希伯索斯被无情的抛入大海,数学的又一巨大进步就这样拉开了序幕!
情景引入
温故新知
1.我们学过的数有哪些?
小学学过自然描数、小数、分数,进入初中又学习了负数
2.什么叫做有理数
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如 , , 5.2, …
负分数:如 , ,-3.5, …
有理数
1.什么叫有理数?
除了有理数外还有没有其它的数呢?
活动一:拼图实践
将两个边长为1的小正方形,剪一剪,拼一拼,
设法得到一个大正方形
1
1
1
1
①
②
③
④
①
②
③
④
设大正方形的边长为 a ,则 a 满足什么条件?
a
探究新知
张师傅在铺地板时,想设法用两个面积为1的正方形地板砖,通过拼的方法得到一个面积为2的正方形,你能帮张师傅解决这一问题吗?
1
1
1
1
1
1
1
1
思考:无论以什么样的方式拼接,你所得到的大正方形的面积是多少?
1
1
1
1
1
1
1
1
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
问题1 设大正方形的边长为a,则a满足什么条件?
∵ S大正方形=2,∴ a2=2。
探究问题一:无理数的存在性
问题2:a是一个什么样的数?a可能是整数吗?
从“数”的角度:
∵ a2=2, 而12=1, 22=4 ,
∴ 12
探究问题一:无理数的存在性
从“形”的角度:
取出一个三角形
∵在三角形ABC中,AC=1,AB=1,BC=a;
根据三角形的三边关系:
AC-AB< a
问题3:a可能是分数吗?
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
探究问题一:无理数的存在性
问题3:a可能是分数吗?
问题4:根据问题2、3的结果, 你得到什么结论?
归纳:a既不是整数,也不是分数,所以a不是有理数。
探究问题一:无理数的存在性
问题2:a是一个什么样的数?a可能是整数吗?
质疑问题 a 究竟是多少?
1
面积为2
a
2
a的整数部分是几?十分位是几?百分位呢?
探究问题二:估算无理数的近似值
1、小组内讨论如何确定a的个位数、十分位、百分位、千分位的大小,总结方法;
2、组长带领组员交流讨论在预习过程中遇到的问题并订正导案中的内容;
3、把未解决问题贴到黑板上;
交流讨论
下列数哪些是有理数 哪些是无理数
3.14159,
-5.232 332…,
123.345 678 910 11…(由相继的正整数组成).
(1)有限小数是有理数; ( )
(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )
(4)有理数是有限小数. ( )
判断题
╳
√
√
╳
右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.试分别找出两条长度是有理数的线段和两条长度是无理数的线段.
1、无理数的存在性
2、估计无理数的近似值
无限逼近法
3、数的分类
小结
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
