24.1.3

课件12张PPT。义务教育课程标准实验教科书九年级 上册人民教育出版社24.1.3弧、弦、圆心角
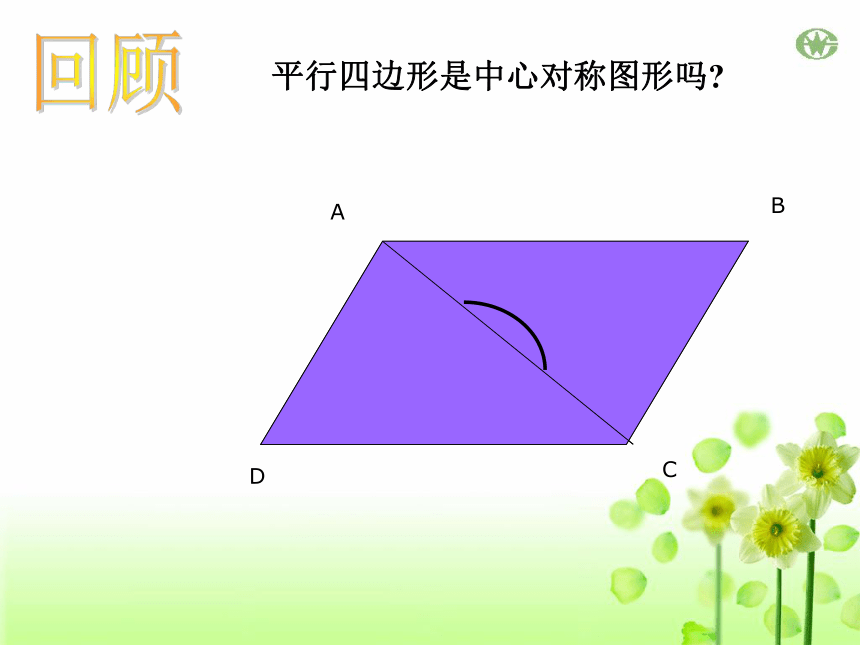
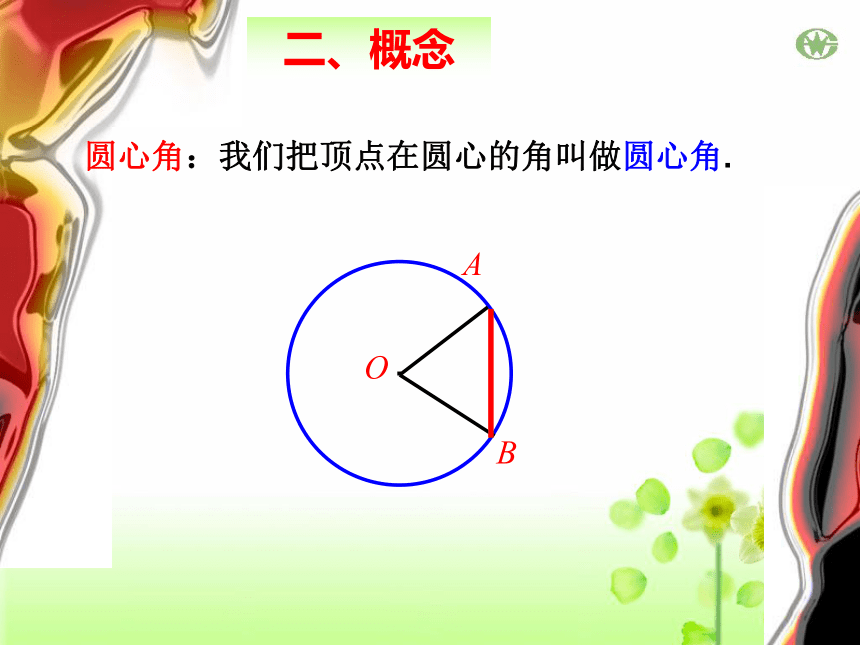
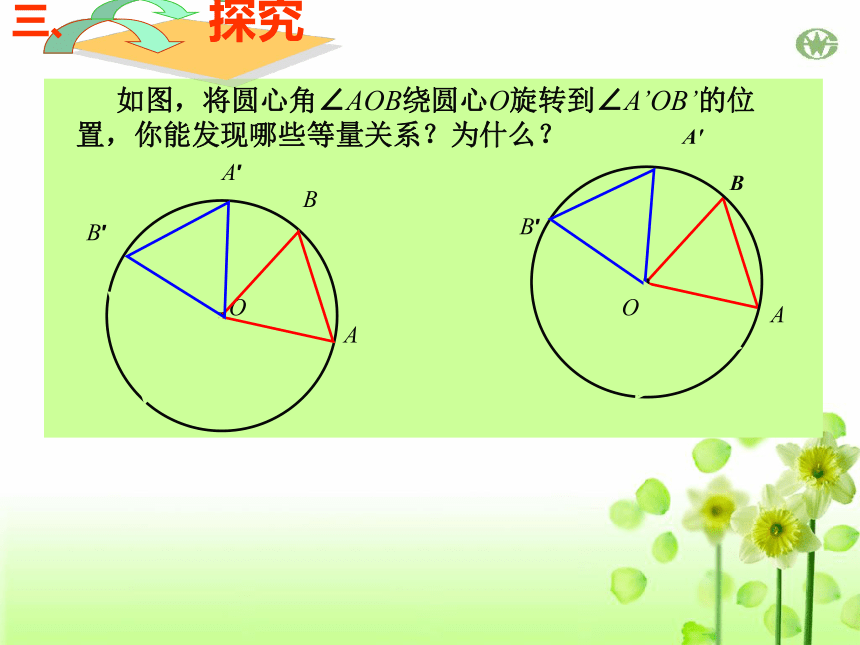
ABCDO回顾平行四边形是中心对称图形吗?圆是中心对称图形吗?它的对称中心在哪里?·一、思考圆是中心对称图形，它的对称中心是圆心.旋转不变性· 圆心角：我们把顶点在圆心的角叫做圆心角.O二、概念 如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？·OABOA′B′三、同样，还可以得到：
在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角_____， 所对的弦________；
在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角______，所对的弧_________．在同圆或等圆中，相等的圆心角
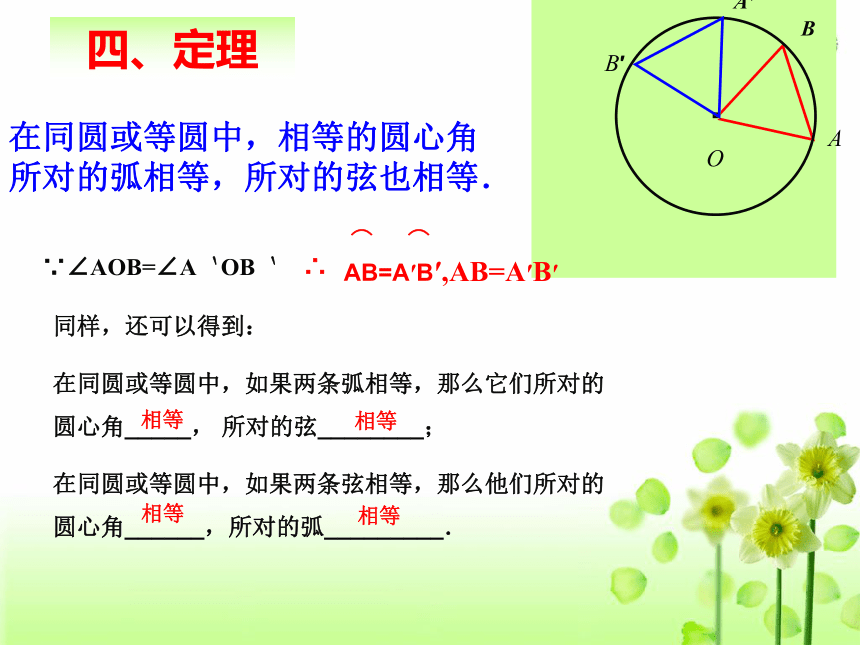
所对的弧相等，所对的弦也相等．相等相等相等相等四、定理·OABA′B′∵∠AOB=∠A｀OB｀·OABA′B′圆心角定理及推广定理：即：同圆或等圆中 ⌒ ⌒
AB=A′B′∠AOB＝∠A′OB′知
1
得
2
1.如图，AB、CD是⊙O的两条弦．
（1）如果AB=CD，那么___________，_________________．
（2）如果 ，那么____________，______________．
（3）如果∠AOB=∠COD，那么_____________，____________．
（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？AB=CDAB=CD相 等 ∵AB=CD ，∴∠AOB=∠COD. 又∵AO=CO，BO=DO， ∴△AOB≌ △COD. ∵OE 、OF是AB与CD对应边上的高，∴ OE = OF.五、定理巩固练习 ⌒ ⌒
AB = CD ⌒ ⌒
AB = CD ⌒ ⌒
AB = CD·ABCO六、例题如图，AB是⊙O的直径， ∠COD=35°，
求∠AOE的度数． ⌒ ⌒
BC = CD ⌒
= DE, 练习1 如图，已知
求证：AB=CD变式：如图，如果AD=BC，求证：AB=CD例题2 ⌒ ⌒
AD=BC 如图，已知AB、CD是⊙O中互相垂直的两条直径，又两条弦AE、CF垂直相交与点G，
证明：AE=CFP例题3