14.3 等腰三角形(江苏省宿迁市沭阳县)
文档属性
| 名称 | 14.3 等腰三角形(江苏省宿迁市沭阳县) |  | |
| 格式 | rar | ||
| 文件大小 | 100.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-14 21:26:00 | ||
图片预览

文档简介
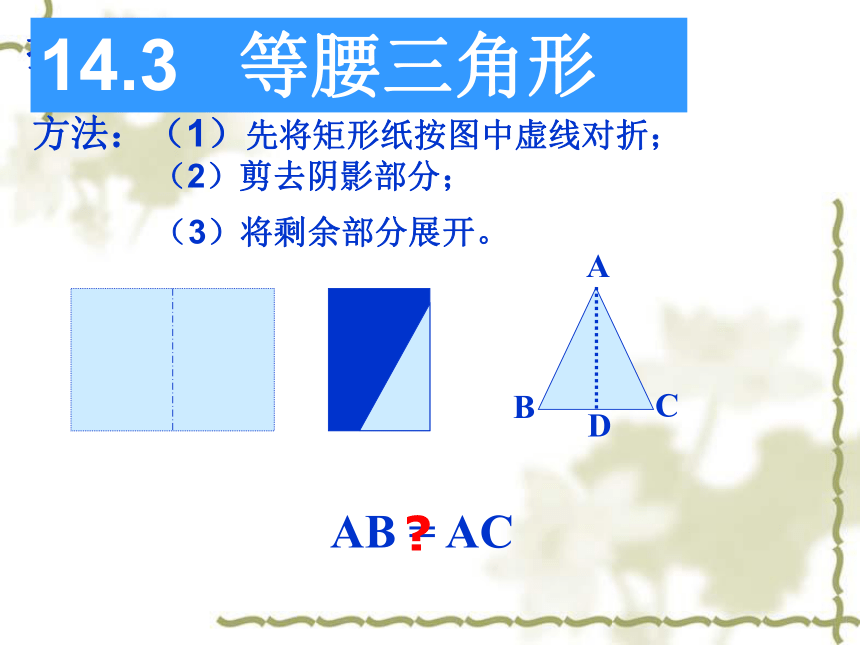
课件13张PPT。欢迎各位老师莅临指导授课人: 王倩倩方法:(1)先将矩形纸按图中虚线对折;
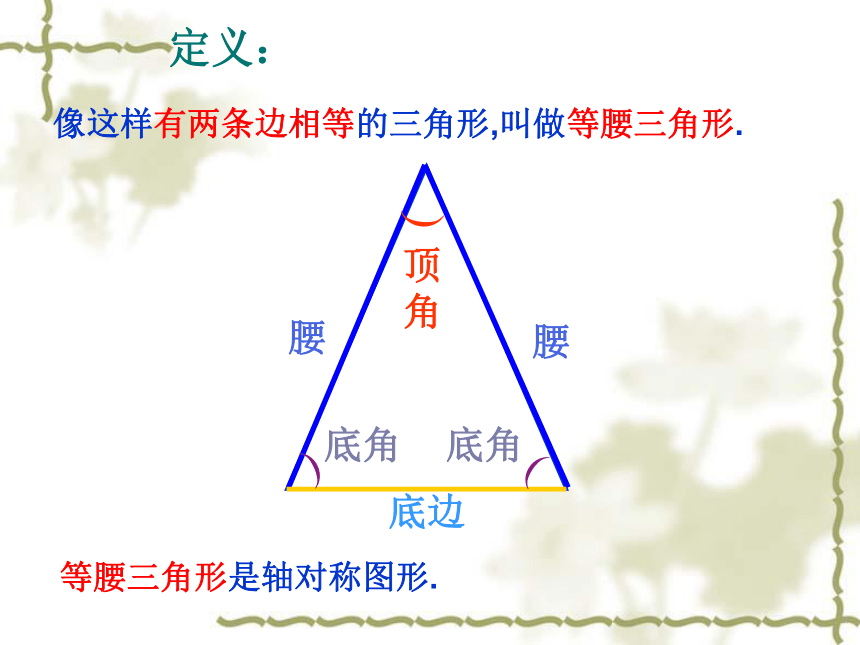
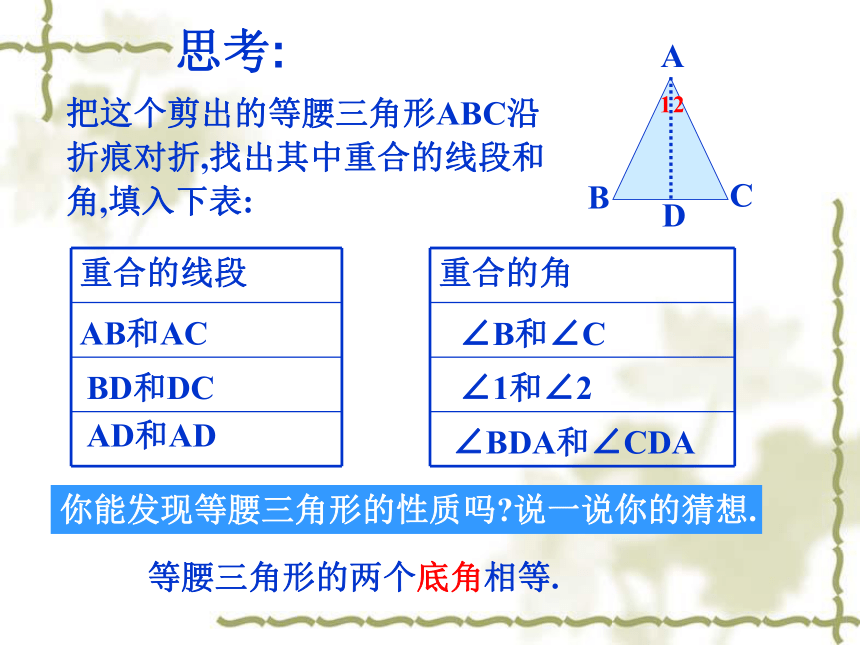
(2)剪去阴影部分; (3)将剩余部分展开。探究:AB = AC14.3 等腰三角形?顶角底边(定义:等腰三角形是轴对称图形.像这样有两条边相等的三角形,叫做等腰三角形.思考:把这个剪出的等腰三角形ABC沿
折痕对折,找出其中重合的线段和
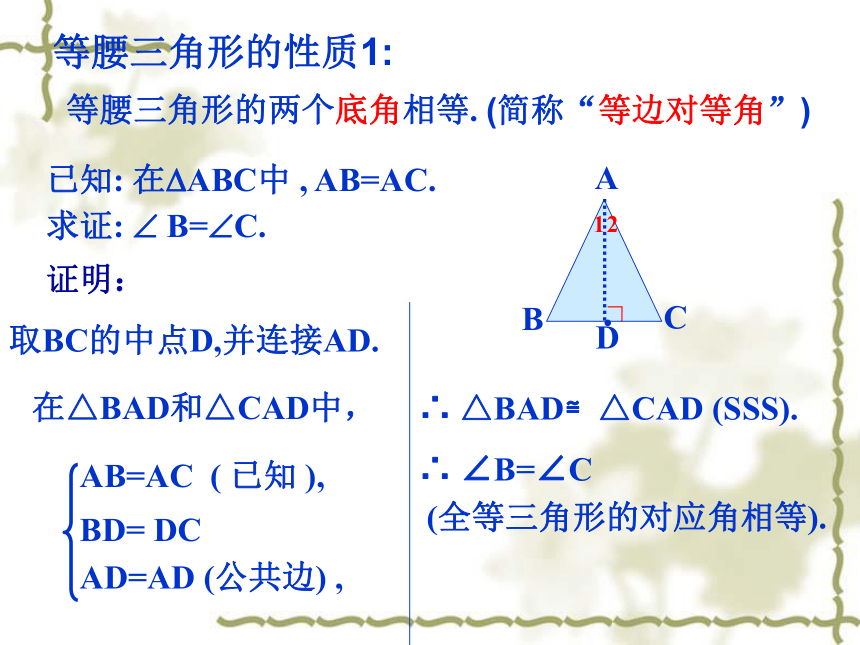
角,填入下表:你能发现等腰三角形的性质吗?说一说你的猜想.AB和ACBD和DCAD和AD∠B和∠C∠1和∠2∠BDA和∠CDA等腰三角形的两个底角相等.D等腰三角形的性质1:等腰三角形的两个底角相等.(简称“等边对等角”)证明:取BC的中点D,并连接AD. 在△BAD和△CAD中,AB=AC ( 已知 ),BD= DC AD=AD (公共边) ,∴ △BAD≌△CAD (SSS).∴ ∠B=∠C
(全等三角形的对应角相等).·已知: 在?ABC中 , AB=AC.
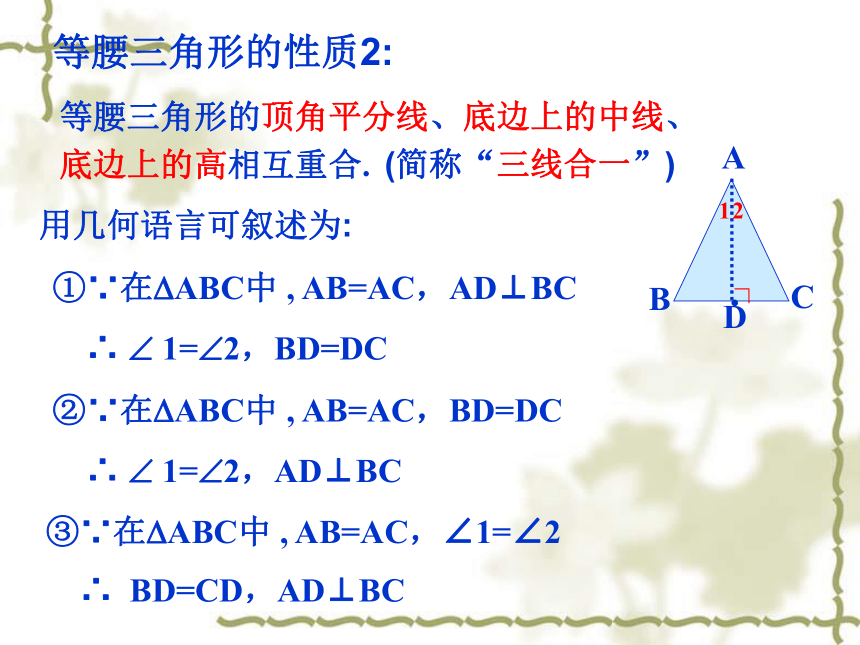
求证: ? B=?C.∟等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.用几何语言可叙述为:①∵在?ABC中 , AB=AC,AD⊥BC
∴ ? 1=?2,BD=DC②∵在?ABC中 , AB=AC,BD=DC
∴ ? 1=?2,AD⊥BC③∵在?ABC中 , AB=AC,∠1=∠2
∴ BD=CD,AD⊥BC(简称“三线合一”)∟(3)若等腰三角形的一个角是70°,
则它的另外两个角分别是 .(1)若等腰三角形的顶角是70°,则它的底角是 .练一练55°(4)若等腰三角形的一个角是120°,
则它的另外两个角分别是 .30°和30°或70°和40°55°和55°(2)若等腰三角形的底角是70°,则它的顶角是 .40°(5)在△ABC中,AB=AC,∠BAC=90°,
BC=4, AD是BC边上的高,则
∠BAD= ,
BD= .练一练45°2 例1:如图,在三角形ABC中,AB=AC,点D在AC上,且BC=BD=AD,求△ABC各角的度数.解:∵AB=AC
∴∠ABC=∠C(等边对等角)∵BC=BD
∴∠C=∠2(等边对等角)∵BD=AD
∴∠A=∠1(等边对等角)设∠A=x,则有
∠2=∠A+∠1=2x则∠C=∠ABC=2x在△ABC中,
∠A+∠ABC+∠C= 180° 即x + 2x + 2x =180°解得 x =36°∴在△ABC中,
∠A=36°,∠ABC=∠C=72°.∠1=xxx2x2xE 在△ABC中, AB=AC, ∠A=36° ,请同学们想一想,如何添一条线,将等腰三角形ABC分成两个等腰三角形?只要做∠B的角平分线即可!ABCD只要再做∠BDE的角平分线即可!以下步骤重复下去即可! 如何再添一条线,可多得到一个等腰三角形?还可以继续吗?趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,
求∠MEF的度数。ABCDEFMN15°15°30°30°45°45°60°60°75°小结:2.等腰三角形是轴对称图形.1.有两条边相等的三角形,叫做等腰三角形.(1)等腰三角形的两个底角相等(等边对等角).3.等腰三角形的性质:(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.(三线合一)作业课本143页
第1题
第3题
(2)剪去阴影部分; (3)将剩余部分展开。探究:AB = AC14.3 等腰三角形?顶角底边(定义:等腰三角形是轴对称图形.像这样有两条边相等的三角形,叫做等腰三角形.思考:把这个剪出的等腰三角形ABC沿
折痕对折,找出其中重合的线段和
角,填入下表:你能发现等腰三角形的性质吗?说一说你的猜想.AB和ACBD和DCAD和AD∠B和∠C∠1和∠2∠BDA和∠CDA等腰三角形的两个底角相等.D等腰三角形的性质1:等腰三角形的两个底角相等.(简称“等边对等角”)证明:取BC的中点D,并连接AD. 在△BAD和△CAD中,AB=AC ( 已知 ),BD= DC AD=AD (公共边) ,∴ △BAD≌△CAD (SSS).∴ ∠B=∠C
(全等三角形的对应角相等).·已知: 在?ABC中 , AB=AC.
求证: ? B=?C.∟等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.用几何语言可叙述为:①∵在?ABC中 , AB=AC,AD⊥BC
∴ ? 1=?2,BD=DC②∵在?ABC中 , AB=AC,BD=DC
∴ ? 1=?2,AD⊥BC③∵在?ABC中 , AB=AC,∠1=∠2
∴ BD=CD,AD⊥BC(简称“三线合一”)∟(3)若等腰三角形的一个角是70°,
则它的另外两个角分别是 .(1)若等腰三角形的顶角是70°,则它的底角是 .练一练55°(4)若等腰三角形的一个角是120°,
则它的另外两个角分别是 .30°和30°或70°和40°55°和55°(2)若等腰三角形的底角是70°,则它的顶角是 .40°(5)在△ABC中,AB=AC,∠BAC=90°,
BC=4, AD是BC边上的高,则
∠BAD= ,
BD= .练一练45°2 例1:如图,在三角形ABC中,AB=AC,点D在AC上,且BC=BD=AD,求△ABC各角的度数.解:∵AB=AC
∴∠ABC=∠C(等边对等角)∵BC=BD
∴∠C=∠2(等边对等角)∵BD=AD
∴∠A=∠1(等边对等角)设∠A=x,则有
∠2=∠A+∠1=2x则∠C=∠ABC=2x在△ABC中,
∠A+∠ABC+∠C= 180° 即x + 2x + 2x =180°解得 x =36°∴在△ABC中,
∠A=36°,∠ABC=∠C=72°.∠1=xxx2x2xE 在△ABC中, AB=AC, ∠A=36° ,请同学们想一想,如何添一条线,将等腰三角形ABC分成两个等腰三角形?只要做∠B的角平分线即可!ABCD只要再做∠BDE的角平分线即可!以下步骤重复下去即可! 如何再添一条线,可多得到一个等腰三角形?还可以继续吗?趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,
求∠MEF的度数。ABCDEFMN15°15°30°30°45°45°60°60°75°小结:2.等腰三角形是轴对称图形.1.有两条边相等的三角形,叫做等腰三角形.(1)等腰三角形的两个底角相等(等边对等角).3.等腰三角形的性质:(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.(三线合一)作业课本143页
第1题
第3题
