数学人教A版（2019）选择性必修第一册1.1.2空间向量的数量积运算（共31张ppt）

(共31张PPT)
空间向量的数量积运算
由于任意两个空间向量都可以通过平移转化为同一平面内的向量，因此，两个平面向量的夹角和数量积就可以像平面向量那样来定义.
复习引入
向量的夹角与数量积的概念
如果一个物体在力 的作用下产生位移 ，那么力 所做的功 .
为了在数学中体现“功”这样一个标量，我们引进了“数量积”的概念.
情境设置
新知学习
问题1：. 是哪两个量的夹角？
[答案] 是力 与位移 的夹角.
问题2：.任意两个向量的数量积是向量吗？两个向量的数量积一定是非负数吗？
[答案] 不是向量，两个向量的数量积是实数，不一定是非负数.
问题3：如图所示，空间四边形的各边和对角线长均等于 ， 是 的中点，则下列说法正确的是哪些？
（1） ；（2） ；（3） .
[答案] 是 的中点， ， ，即 ， 错误；
由题意知 与 的夹角为 ， ，
由题意知 与 的夹角为 ， ，∴（2）错误；
是 的中点，且 是正三角形， ，
.
，∴（3）正确.
综上，只有（3）正确.
1.定义：如图，已知两个非零向量 ， ，在空间任取一点 ，作 ， ，则________叫作向量 ， 的夹角，记作_________.


2.空间向量的数量积
已知两个向量 和 ，则 叫作 ， 的数量积，记作 .即 .特别地，零向量与任意向量的数量积为0.
向量的夹角与数量积的概念
数量积的运算性质
①a·e=|a|cos(e为单位向量).
②若a,b是非零向量,则a⊥b a·b=0;
③若a与b同向,则a·b=|a||b|;
若a与b反向,则a·b=-|a||b|.
特别地,|a|2=a·a或|a|= .
④若θ为a,b的夹角,则cos θ= .
⑤|a·b|≤|a||b|(当且仅当a,b共线时,等号成立)
空间向量数量积的运算律
问题1：.“若 ，则 ”，这种说法正确吗？
[答案] 不正确，向量不能约分.
问题2：数量积的运算满足除法吗？
[答案] 数量积的运算不满足除法，即对于向量 ， ，若 ，不能得到
（或 ）.例如当非零向量 ， 垂直时， ，但 显然是没有意义的.
情境设置
问题3：数量积的运算不满足结合律吗？
[答案] 向量的数量积的运算不满足结合律，即 不一定等于 .
1.空间向量数量积的运算律
（1）交换律： ；
（2）分配律： ；
（3） .
2.空间向量数量积的有关结论
（1） ；
（2） ；
（3） .
空间向量数量积的运算律
投影向量
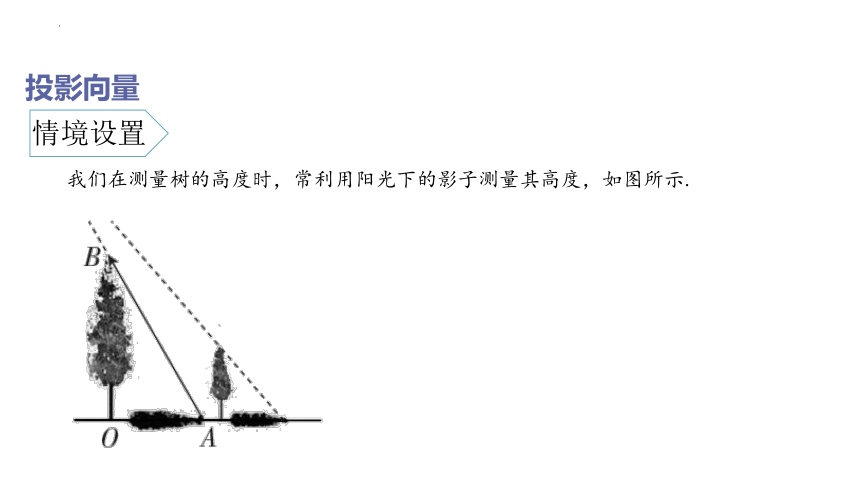
我们在测量树的高度时，常利用阳光下的影子测量其高度，如图所示.
情境设置
问题1：若测得 ，如何求 在 上的投影？
[答案] 根据平面数量积的几何意义， 在 上的投影为 .
问题2：平面向量数量积的投影定义，在空间中还成立吗？
[答案] 根据空间向量数量积公式可知，依然成立.
1.如图（1），在空间中，向量 向向量 投影，先将它们平移到同一个平面 内，利用平面上向量的投影，得到与向量 共线的向量 ， · , ，向量 称为向量 在向量 上的投影向量.类似地，也可以将向量 向直线 投影，如图（2）.
投影向量
2.如图（3），向量 向平面 投影，就是分别由向量 的起点 和终点 作平面 的垂线，垂足分别为 ， ，得到向量_______，向量_______称为向量 在平面 上的投影向量.这时，向量____，_ ______的夹角就是向量 所在直线与平面 所成的角.




C'
D'
B'
A'
C
D
A
B
◆练习 已知正方体AC'边长为1,求：
数量积 等于 的长度 与 在
的方向上的投影 的乘积。
θ
B1
B
O
A
几何意义
如图，在直三棱柱ABC A1B1C1中，∠BCA＝90°，CA＝CB＝1，棱AA1＝2，点N为AA1的中点．
求cos〈，〉的值．
解　因为＝－＝＋－， ＝＋，
所以||2＝()2＝2＋2＋2＝12＋22＋12＝6，||＝，
||2＝(＋)2＝2＋2＝12＋22＝5，||＝，
＝()·()＝2－2＝22－12＝3，
所以cos〈，〉＝＝＝
利用数量积求夹角
求两个非零向量夹角的两种途径
(1)转化求角：把向量夹角转化为平面几何中的对应角，利用解三角形的知识求解．
(2)利用数量积求夹角的余弦值：cos〈，〉=
方法总结
问题 如右图，在平行六面体ABCD－A'B'C'D'中，AB = 5，
AD = 3，AA'= 7，∠BAD = 60°，∠BAA'= ∠DAA'= 45°. 求：
(1) ；(2) AC'的长（精确到0.1）.
追问(1) 如何计算 ？它们的长度，夹角是多少？
AB，AD的长度和夹角均已知，AB＝5，AD＝3，
∠BAD = 60°.
解：(1)
追问(2) 为了求AC'的长，应该用哪些向量表示 ？为什么？如何表示？
可以根据已知条件与平行四边形法则，用
来表示，因为它们的模长和夹角均已知，可以进行数量积运算.
(2)
用已知向量表示所求向量，再由数量积运算求模长，是立体几何中求线段长度的常用向量方法.
例 如图，m,n是平面内的两条相交直线，如果m, l n,求证：l
m
n
l
方法：线面垂直的定义（l 内的任意一条直线）
思考
（1）如何把已知的几何元素转化为向量表示？
（2）一些未知的几何元素能否用已知向量表示？
（3）结论和已经表示出来的向量或其运算有何联系？能否通过向量的运算获得结论？
（4）如何将向量运算的结果“翻译”为几何结论？
共面向量定理
方法一：向量法
m
n
l
证明：
在平面内任取不与m,n重合的直线g，
在直线l,g,m,n上取向量l,g,m,n
因为m,n相交，所以m,n不平行，由共面向量定理得，
存在唯一的实数对(x, y),使g=xm+yn
l·g= l · xm+ l · yn= x (l · m)+ y (l · n)
∵ m, l n ∴l · m=0, l · n=0
∴l · g =0即l g
∴ g，即垂直于平面内的任意一条直线，l
g
l
n
m
g
【用向量解决几何问题的常用方法（三部曲）】
选择恰当的向量表示问题中的几何元素
通过向量运算得出几何元素的关系
把运算结果“翻译”成相应的几何意义
方法二：几何法
m
n
l
证明：
假设l不垂直于平面，则l与平行，或l与斜交
情形1：l与平行
∵ l/，过l的任意平面相交于直线g, l/
∵ m ∴m
g
∵ n ∴n
∴ m/,与已知矛盾
方法一：几何法
m
n
l
证明：
情形2：l与斜交
设l与交点为O，
O
过O点作直线g ， 则g平面
∵ m ∴n
∴ m/,与已知矛盾
g
利用向量的数量积求两异面直线所成角
典例如图,在直三棱柱ABC -A1B1C1中,∠ABC=90°,
AB=BC=1,AA1= ,求异面直线BA1与AC所成角的余弦值.
【规范答题】
课堂小结
谢 谢！