人教版版九年级上册》第二十四章 圆》直线和圆的位置关系
文档属性
| 名称 | 人教版版九年级上册》第二十四章 圆》直线和圆的位置关系 |  | |
| 格式 | rar | ||
| 文件大小 | 303.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-12 12:23:00 | ||
图片预览



文档简介
课件13张PPT。第二课时:
直线和圆的位置关系要点、考点1.直线和圆的位置关系.设⊙O的半径为r,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交? d<r
(2)直线l和⊙O相切? d=r
(3)直线l和⊙O相离? d>r 2、切线的判定和性质定理及推论.
(1)切线的判定定理:经过半径的外端并且垂直
于这条半径的直线是圆的切线.
(2)切线的性质定理及其推论.定理:圆的切线垂直于经过切点的半径.
推论1:经过圆心且垂直于切线的直线必经过切点.
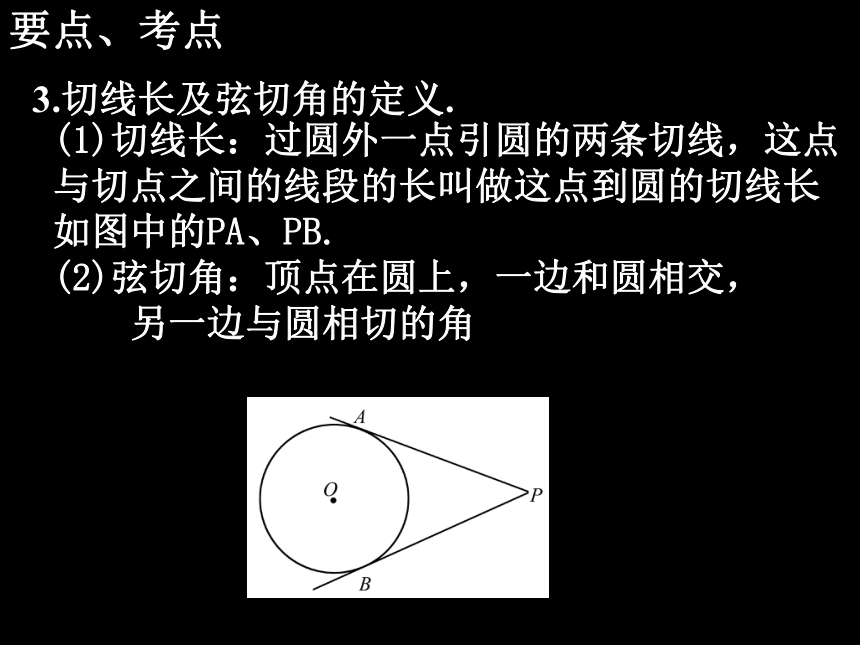
推论2:经过切点且垂直于切线的直线必经过圆心. 3.切线长及弦切角的定义. (1)切线长:过圆外一点引圆的两条切线,这点与切点之间的线段的长叫做这点到圆的切线长如图中的PA、PB.
(2)弦切角:顶点在圆上,一边和圆相交,
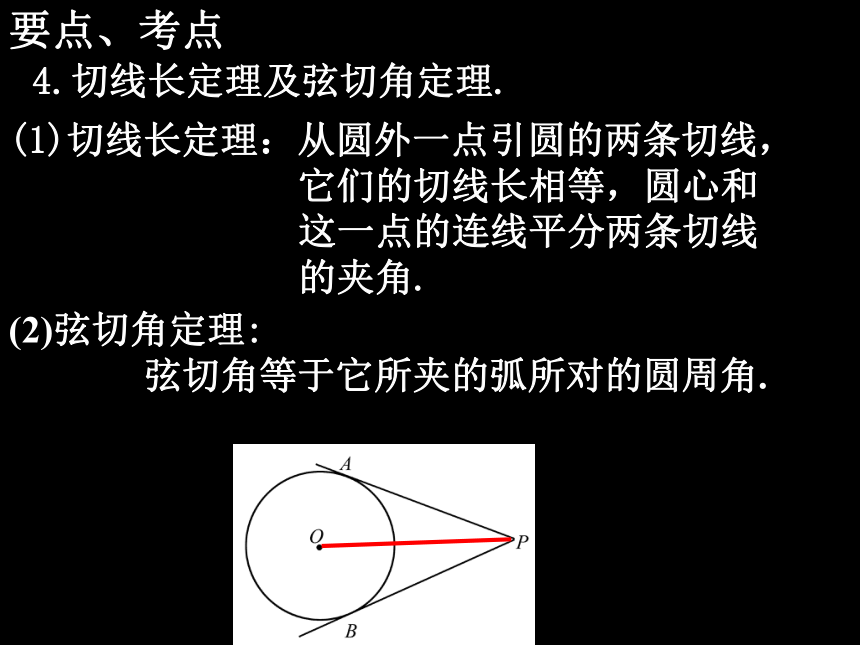
另一边与圆相切的角要点、考点4.切线长定理及弦切角定理.(1)切线长定理:从圆外一点引圆的两条切线,
它们的切线长相等,圆心和
这一点的连线平分两条切线
的夹角.(2)弦切角定理:
弦切角等于它所夹的弧所对的圆周角. 要点、考点(4)四边形的内切圆的性质:
圆外切四边形的对边和相等. 要点、考点5.三角形的内切圆和四边形的内切圆.(1)三角形的内切圆:和三角形各边都相切的圆. (2)三角形内心:内切圆的圆心.(3)三角形内切圆的性质:
①到三角形三边的距离相等,
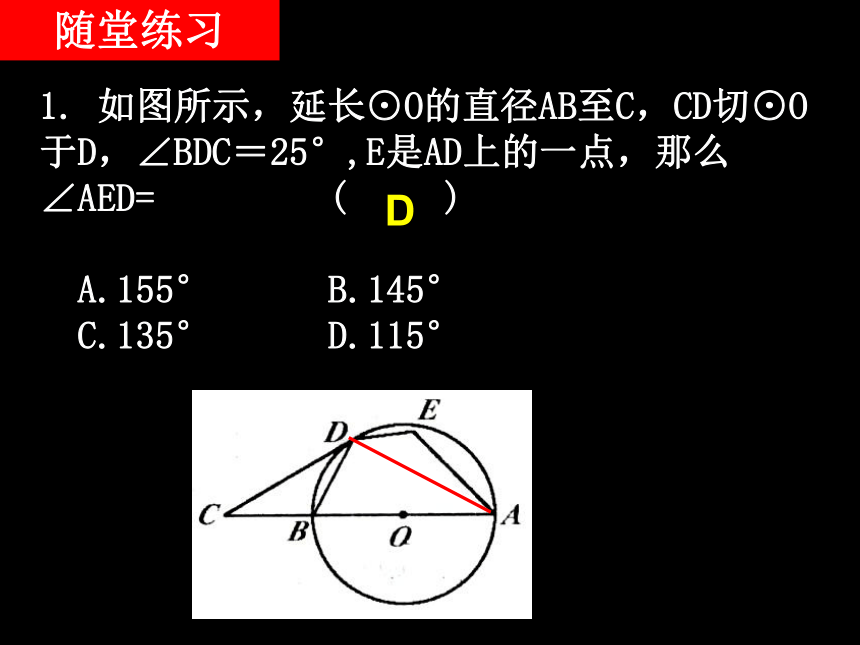
②圆心和三角形各顶点的连线平分这个角.1. 如图所示,延长⊙O的直径AB至C,CD切⊙O于D,∠BDC=25°,E是AD上的一点,那么∠AED= ( )
A.155° B.145°
C.135° D.115° D随堂练习2.下列命题中,正确的命题有( )
①圆的切线垂直于半径
②垂直于切线的直径必过圆心
③经过圆心且垂直于切线的直线过切点
④如果圆的两条切线平行,那么过两切点的直线
必过圆心
⑤三角形的内心不一定在三角形的内部
⑥多边形的内切圆圆心到各边的距离相等
A.2个 B.3个
C.4个 D.5个
B随堂练习3.等腰梯形外切于⊙O,⊙O的直径为6 cm,等腰梯形的腰长为8 cm,则梯形的面积为( )
A.24 cm2 B.48 cm2
C.36 cm 2 D.无法计算B随堂练习4.如图,AB、AC是⊙O的两条切线,B、C是切点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.65° B.115°
C.65°或115° D.130°或50°C随堂练习5.如图,BC为半圆的直径,CA为切线,AB交半圆于E,EF⊥BC于F,连结EC,则图中与△EFC相似的三角形共有 ( )
A.1个 B.2个
C.3个 D.4个D随堂练习【例1】如图,在△ABC中,AC=BC,E是内心,
AE的延长线交△ABC的外接圆于D,
求证:
(1)BE=AE
(2)AB/AC=AE/DE典型例题解析【解析】
(1)要证BE=AE,则需证∠1=∠2,
由AC=BC?∠CAB=∠CBA,
想到AE、BE必是角平线,而E是内心,
所以AE、BE分别平分∠CAB、∠CBA.(2)要证比例式,应该先想到这几条线段在哪两个三角形中,再证相似,这是证明比例式(或等积式)的首选数学思路.但此题的四条线段不在两个三角形中,下面考虑的思路有两条:
一是等线段代换,
二是中间比.此题中若将AE换成BE,
则只要证△ABC∽△BED.ΔABC∽ΔBED2.(2006内蒙古)如图在△ABC中,AB=AC=5,以AB为直径的⊙P交BC于H,点A,B在x轴上,B点的坐标为(1,0)(1)求点A.H.C的坐标;(2)过H作AC的垂线交AC于E,交x轴于F,求证:EF是P的切线。(3)求经过A.O两点且顶点到x轴的距离等于4的抛物线的解析式。AyxCBoPHEF
直线和圆的位置关系要点、考点1.直线和圆的位置关系.设⊙O的半径为r,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交? d<r
(2)直线l和⊙O相切? d=r
(3)直线l和⊙O相离? d>r 2、切线的判定和性质定理及推论.
(1)切线的判定定理:经过半径的外端并且垂直
于这条半径的直线是圆的切线.
(2)切线的性质定理及其推论.定理:圆的切线垂直于经过切点的半径.
推论1:经过圆心且垂直于切线的直线必经过切点.
推论2:经过切点且垂直于切线的直线必经过圆心. 3.切线长及弦切角的定义. (1)切线长:过圆外一点引圆的两条切线,这点与切点之间的线段的长叫做这点到圆的切线长如图中的PA、PB.
(2)弦切角:顶点在圆上,一边和圆相交,
另一边与圆相切的角要点、考点4.切线长定理及弦切角定理.(1)切线长定理:从圆外一点引圆的两条切线,
它们的切线长相等,圆心和
这一点的连线平分两条切线
的夹角.(2)弦切角定理:
弦切角等于它所夹的弧所对的圆周角. 要点、考点(4)四边形的内切圆的性质:
圆外切四边形的对边和相等. 要点、考点5.三角形的内切圆和四边形的内切圆.(1)三角形的内切圆:和三角形各边都相切的圆. (2)三角形内心:内切圆的圆心.(3)三角形内切圆的性质:
①到三角形三边的距离相等,
②圆心和三角形各顶点的连线平分这个角.1. 如图所示,延长⊙O的直径AB至C,CD切⊙O于D,∠BDC=25°,E是AD上的一点,那么∠AED= ( )
A.155° B.145°
C.135° D.115° D随堂练习2.下列命题中,正确的命题有( )
①圆的切线垂直于半径
②垂直于切线的直径必过圆心
③经过圆心且垂直于切线的直线过切点
④如果圆的两条切线平行,那么过两切点的直线
必过圆心
⑤三角形的内心不一定在三角形的内部
⑥多边形的内切圆圆心到各边的距离相等
A.2个 B.3个
C.4个 D.5个
B随堂练习3.等腰梯形外切于⊙O,⊙O的直径为6 cm,等腰梯形的腰长为8 cm,则梯形的面积为( )
A.24 cm2 B.48 cm2
C.36 cm 2 D.无法计算B随堂练习4.如图,AB、AC是⊙O的两条切线,B、C是切点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A.65° B.115°
C.65°或115° D.130°或50°C随堂练习5.如图,BC为半圆的直径,CA为切线,AB交半圆于E,EF⊥BC于F,连结EC,则图中与△EFC相似的三角形共有 ( )
A.1个 B.2个
C.3个 D.4个D随堂练习【例1】如图,在△ABC中,AC=BC,E是内心,
AE的延长线交△ABC的外接圆于D,
求证:
(1)BE=AE
(2)AB/AC=AE/DE典型例题解析【解析】
(1)要证BE=AE,则需证∠1=∠2,
由AC=BC?∠CAB=∠CBA,
想到AE、BE必是角平线,而E是内心,
所以AE、BE分别平分∠CAB、∠CBA.(2)要证比例式,应该先想到这几条线段在哪两个三角形中,再证相似,这是证明比例式(或等积式)的首选数学思路.但此题的四条线段不在两个三角形中,下面考虑的思路有两条:
一是等线段代换,
二是中间比.此题中若将AE换成BE,
则只要证△ABC∽△BED.ΔABC∽ΔBED2.(2006内蒙古)如图在△ABC中,AB=AC=5,以AB为直径的⊙P交BC于H,点A,B在x轴上,B点的坐标为(1,0)(1)求点A.H.C的坐标;(2)过H作AC的垂线交AC于E,交x轴于F,求证:EF是P的切线。(3)求经过A.O两点且顶点到x轴的距离等于4的抛物线的解析式。AyxCBoPHEF
同课章节目录
