【高效备课】人教版八(上) 12.2 三角形全等的判定 第1课时 用“SSS”判定三角形全等 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 12.2 三角形全等的判定 第1课时 用“SSS”判定三角形全等 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 791.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:39 | ||
图片预览







文档简介
(共31张PPT)
12.2 三角形全等的判定
第1课时 用“SSS”判定三角形全等
R·八年级上册
新课导入
通过上节课的学习,大家知道:两个三角形全等时,三条对应边相等,三组对应角相等,那么判定两个三角形全等,是否一定需要满足六个条件呢?如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?从这节课开始,我们来探究全等三角形的判定.
学习目标:
1.通过三角形的稳定性,体验三角形全等的
“边边边”条件.
2.会运用“边边边”定理判定两个三角形的
全等.
推进新课
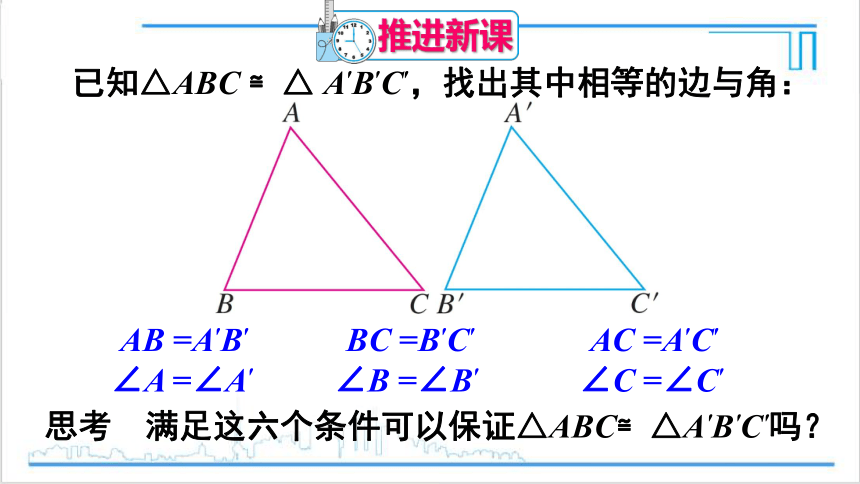
∠A =∠A′
AB =A′B′
已知△ABC ≌△ A′B′C′,找出其中相等的边与角:
思考 满足这六个条件可以保证△ABC≌△A′B′C′吗?
∠B =∠B′
BC =B′C′
∠C =∠C′
AC =A′C′
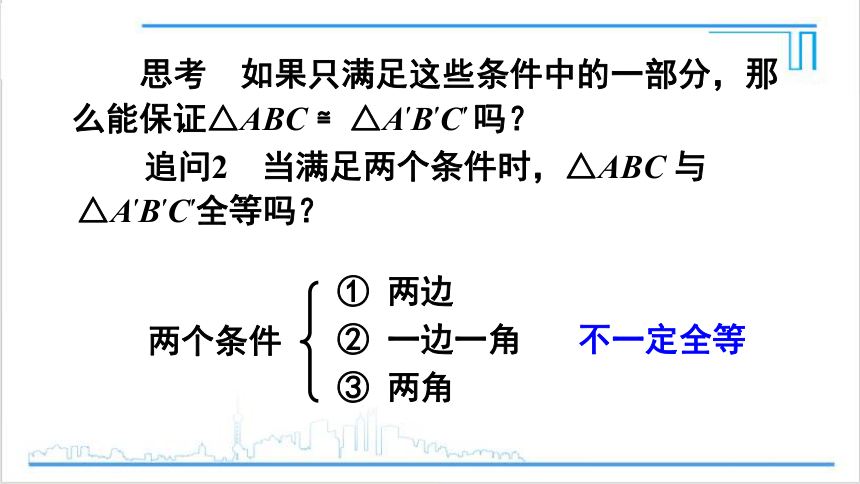
思考 如果只满足这些条件中的一部分,那么能保证△ABC ≌△A′B′C′吗?
追问1 当满足一个条件时,△ABC 与△A′B′C′ 全等吗?
不一定全等
三角形全等的“边边边”条件
知识点
① 两边
② 一边一角
③ 两角
两个条件
思考 如果只满足这些条件中的一部分,那么能保证△ABC ≌△A′B′C′ 吗?
追问2 当满足两个条件时,△ABC 与△A′B′C′全等吗?
不一定全等
① 三边
② 三角
③ 两边一角
④ 两角一边
三个条件
追问3 当满足三个条件时, △ABC 与△A′B′C′ 全等吗?满足三个条件时,又分为几种情况呢?
思考 如果只满足这些条件中的一部分,那么能保证△ABC ≌△A′B′C′吗?
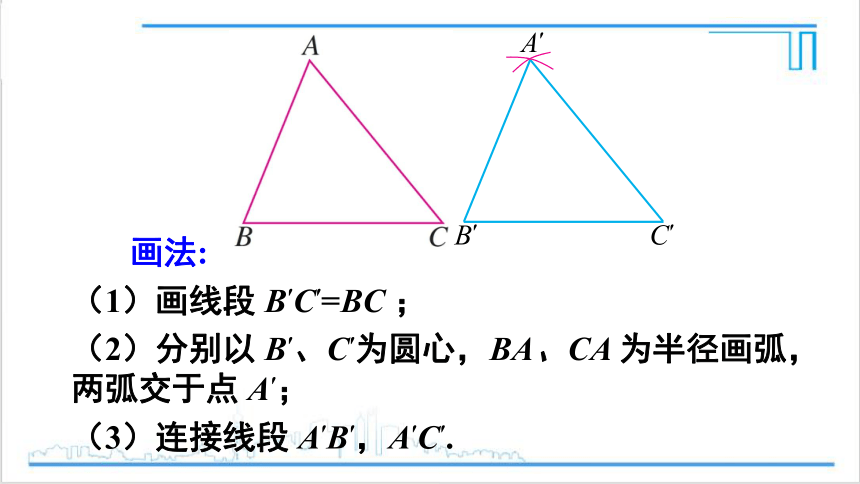
先任意画出一个△ABC,再画出一个△A′B′C′,使 A′B′ = AB,B′C′ = BC,A′C′ = AC.把画好的△A′B′C′ 剪下,放到△ABC上,它们全等吗?
探究
画法:
(1)画线段 B′C′=BC ;
(2)分别以 B′、C′为圆心,BA、CA 为半径画弧,两弧交于点 A′;
(3)连接线段 A′B′,A′C′.
A′
B′
C′
三边分别相等的两个三角形全等.简写为“边边边”或“SSS”.
得出结论
思考 作图的结果反映了什么规律?你能用语言描述一下吗?
可以得到以下基本事实:
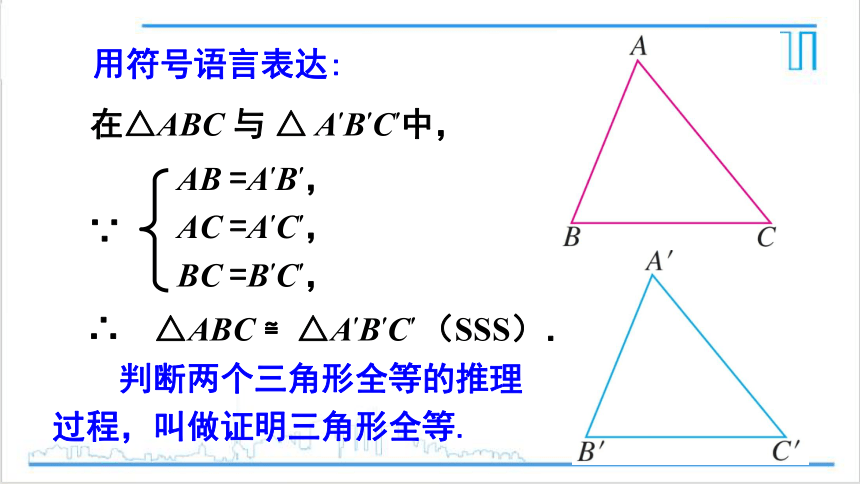
在△ABC 与 △ A′B′C′中,
∴ △ABC ≌△A′B′C′ (SSS).
判断两个三角形全等的推理
过程,叫做证明三角形全等.
AB =A′B′,
AC =A′C′,
BC =B′C′,
∵
用符号语言表达:
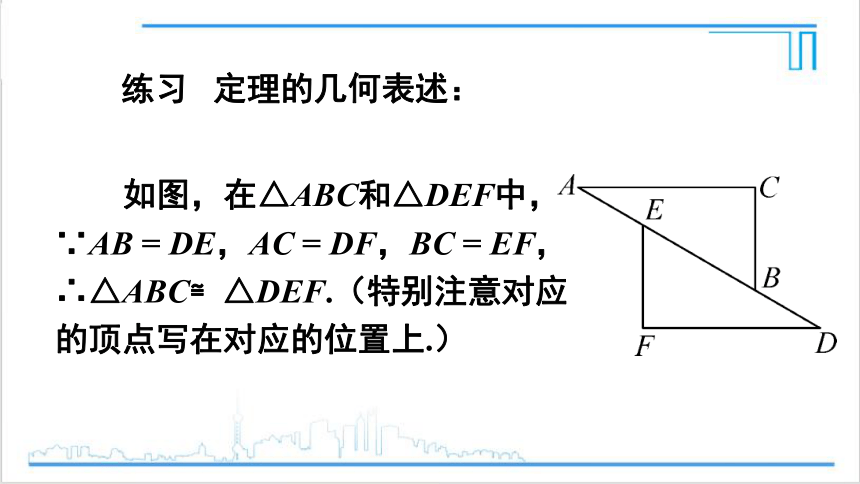
如图,在△ABC和△DEF中,∵AB = DE,AC = DF,BC = EF,∴△ABC≌△DEF.(特别注意对应的顶点写在对应的位置上.)
练习 定理的几何表述:
证明:∵ D 是BC 中点,
∴ BD =DC.
在△ABD 与△ACD 中,
∴ △ABD ≌ △ACD ( SSS ).
例 如图,有一个三角形钢架,AB =AC ,
AD 是连接点 A 与 BC 中点 D 的支架.求证:△ABD ≌△ACD .
AB = AC ,
BD = CD ,
AD = AD ,
∵
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交
OA,OB 于点C、D;
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O′
C′
A′
O
D
B
C
A
作法:
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
作法:
(3)以点C′为圆心,CD 长为半径画弧,与第2 步
中所画的弧交于点D′;
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O′
D′
C′
A′
O
D
B
C
A
作法:
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O′
D′
B′
C′
A′
O
D
B
C
A
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交
OA,OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步
中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
练习 如图,A、D、B、F在一条直线上,BC = DE,AC = EF,BF = AD,求证:△ABC≌△FDE.
证明:∵BF = AD,∴BF + BD = AD + DB,即DF = AB.
在△ABC和△FDE中,
∴△ABC ≌ △FDE(SSS).
随堂演练
1.如图,△ABC中,AB = AC,EB = EC,则由SSS可以判定( )
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
B
基础巩固
2.如图,AB=AD,CB=CD,△ABC 与△ADC全等吗?为什么?
解:全等.∵AB = AD,CB = CD,AC = AC,∴△ABC≌△ADC(SSS).
3.如图,C是AB的中点,AD=CE,CD=BE.求证△ACD≌△CBE.
【课本P37 练习 第1题】
4. 工人师傅常用角尺平分一个任意角。做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合.过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
【课本P37 练习 第2题】
5.如图,点 B、E、C、F 在一条直线上,AB = DE,AC = DF,BE = CF,求证:∠A =∠D.
综合应用
证明:∵BE = CF,∴BE+EC = CF+EC,
即BC = EF,在△ABC 和△DEF 中,
∴△ABC≌△DEF(SSS).
∴∠A =∠D.
6.已知∠AOB,点C是OB边上的一点,用尺规作图,画出经过点C与OA平行的直线.
拓展延伸
解:作图如图所示:
作法:(1)以点 O 为圆心,任意长为半径画弧,分别交OA,OB于点 D,E;
(2)以点 C 为圆心,OD 长为半径画弧,交OB 于点 F;
(3)以点 F 为圆心,DE 长为半径画弧,与第2步中所画的弧相交于点 P ;
(4)过C,P 两点作直线,直线 CP 即为要求作的直线.
课堂小结
A′
B′
C′
判定两个三角形全等:
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
12.2 三角形全等的判定
第1课时 用“SSS”判定三角形全等
R·八年级上册
新课导入
通过上节课的学习,大家知道:两个三角形全等时,三条对应边相等,三组对应角相等,那么判定两个三角形全等,是否一定需要满足六个条件呢?如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?从这节课开始,我们来探究全等三角形的判定.
学习目标:
1.通过三角形的稳定性,体验三角形全等的
“边边边”条件.
2.会运用“边边边”定理判定两个三角形的
全等.
推进新课
∠A =∠A′
AB =A′B′
已知△ABC ≌△ A′B′C′,找出其中相等的边与角:
思考 满足这六个条件可以保证△ABC≌△A′B′C′吗?
∠B =∠B′
BC =B′C′
∠C =∠C′
AC =A′C′
思考 如果只满足这些条件中的一部分,那么能保证△ABC ≌△A′B′C′吗?
追问1 当满足一个条件时,△ABC 与△A′B′C′ 全等吗?
不一定全等
三角形全等的“边边边”条件
知识点
① 两边
② 一边一角
③ 两角
两个条件
思考 如果只满足这些条件中的一部分,那么能保证△ABC ≌△A′B′C′ 吗?
追问2 当满足两个条件时,△ABC 与△A′B′C′全等吗?
不一定全等
① 三边
② 三角
③ 两边一角
④ 两角一边
三个条件
追问3 当满足三个条件时, △ABC 与△A′B′C′ 全等吗?满足三个条件时,又分为几种情况呢?
思考 如果只满足这些条件中的一部分,那么能保证△ABC ≌△A′B′C′吗?
先任意画出一个△ABC,再画出一个△A′B′C′,使 A′B′ = AB,B′C′ = BC,A′C′ = AC.把画好的△A′B′C′ 剪下,放到△ABC上,它们全等吗?
探究
画法:
(1)画线段 B′C′=BC ;
(2)分别以 B′、C′为圆心,BA、CA 为半径画弧,两弧交于点 A′;
(3)连接线段 A′B′,A′C′.
A′
B′
C′
三边分别相等的两个三角形全等.简写为“边边边”或“SSS”.
得出结论
思考 作图的结果反映了什么规律?你能用语言描述一下吗?
可以得到以下基本事实:
在△ABC 与 △ A′B′C′中,
∴ △ABC ≌△A′B′C′ (SSS).
判断两个三角形全等的推理
过程,叫做证明三角形全等.
AB =A′B′,
AC =A′C′,
BC =B′C′,
∵
用符号语言表达:
如图,在△ABC和△DEF中,∵AB = DE,AC = DF,BC = EF,∴△ABC≌△DEF.(特别注意对应的顶点写在对应的位置上.)
练习 定理的几何表述:
证明:∵ D 是BC 中点,
∴ BD =DC.
在△ABD 与△ACD 中,
∴ △ABD ≌ △ACD ( SSS ).
例 如图,有一个三角形钢架,AB =AC ,
AD 是连接点 A 与 BC 中点 D 的支架.求证:△ABD ≌△ACD .
AB = AC ,
BD = CD ,
AD = AD ,
∵
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交
OA,OB 于点C、D;
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O
D
B
C
A
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O′
C′
A′
O
D
B
C
A
作法:
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
作法:
(3)以点C′为圆心,CD 长为半径画弧,与第2 步
中所画的弧交于点D′;
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O′
D′
C′
A′
O
D
B
C
A
作法:
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
O′
D′
B′
C′
A′
O
D
B
C
A
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交
OA,OB 于点C、D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
径画弧,交O′A′于点C′;
(3)以点C′为圆心,CD 长为半径画弧,与第2 步
中所画的弧交于点D′;
(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.
已知:∠AOB.求作: ∠A′O′B′=∠AOB.
用尺规作一个角等于已知角.
练习 如图,A、D、B、F在一条直线上,BC = DE,AC = EF,BF = AD,求证:△ABC≌△FDE.
证明:∵BF = AD,∴BF + BD = AD + DB,即DF = AB.
在△ABC和△FDE中,
∴△ABC ≌ △FDE(SSS).
随堂演练
1.如图,△ABC中,AB = AC,EB = EC,则由SSS可以判定( )
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
B
基础巩固
2.如图,AB=AD,CB=CD,△ABC 与△ADC全等吗?为什么?
解:全等.∵AB = AD,CB = CD,AC = AC,∴△ABC≌△ADC(SSS).
3.如图,C是AB的中点,AD=CE,CD=BE.求证△ACD≌△CBE.
【课本P37 练习 第1题】
4. 工人师傅常用角尺平分一个任意角。做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合.过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
【课本P37 练习 第2题】
5.如图,点 B、E、C、F 在一条直线上,AB = DE,AC = DF,BE = CF,求证:∠A =∠D.
综合应用
证明:∵BE = CF,∴BE+EC = CF+EC,
即BC = EF,在△ABC 和△DEF 中,
∴△ABC≌△DEF(SSS).
∴∠A =∠D.
6.已知∠AOB,点C是OB边上的一点,用尺规作图,画出经过点C与OA平行的直线.
拓展延伸
解:作图如图所示:
作法:(1)以点 O 为圆心,任意长为半径画弧,分别交OA,OB于点 D,E;
(2)以点 C 为圆心,OD 长为半径画弧,交OB 于点 F;
(3)以点 F 为圆心,DE 长为半径画弧,与第2步中所画的弧相交于点 P ;
(4)过C,P 两点作直线,直线 CP 即为要求作的直线.
课堂小结
A′
B′
C′
判定两个三角形全等:
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
