【高效备课】人教版八(上) 12.2 三角形全等的判定 第2课时 用“SAS”判定三角形全等 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 12.2 三角形全等的判定 第2课时 用“SAS”判定三角形全等 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 463.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:39 | ||
图片预览






文档简介
(共29张PPT)
12.2 三角形全等的判定
第2课时用“SAS”判定三角形全等
R·八年级上册
新课导入
上一节课,我们探究了三条边对应相等的两个三角形全等. 如果两个三角形有两条边和一个角分别对应相等,这两个三角形会全等吗?
——这就是本节课我们要探讨的课题.
学习目标:
1.能说出“边角边”判定定理.
2.会用“边角边”定理证明两个三角形全等.
推进新课
问题1 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′ =AB,∠A′=∠A,C′A′= CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
边角边的判定方法
知识点1
探究
A′
D
E
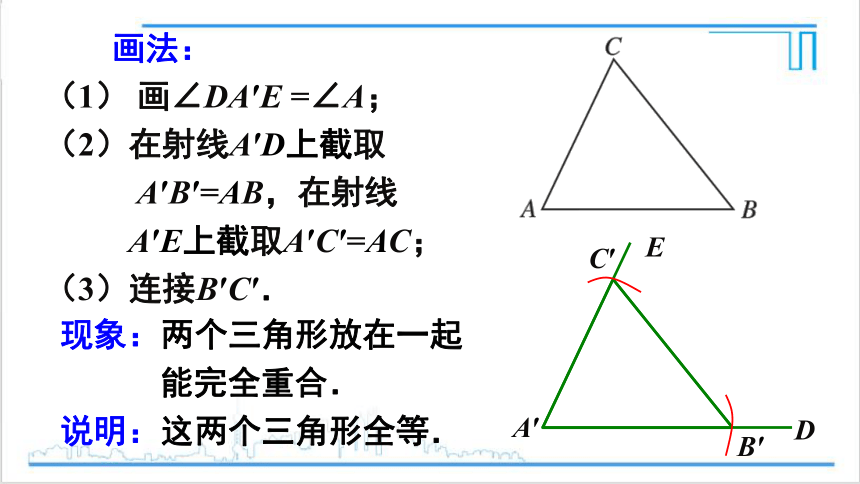
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1) 画∠DA′E =∠A;
(2)在射线A′D上截取
A′B′=AB,在射线
A′E上截取A′C′=AC;
(3)连接B′C′.
B′
C′
几何语言:
在△ABC 和△ A′B′ C′中,
∴ △ABC ≌△ A′B′ C′(SAS).
归纳概括“SAS”判定方法:
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).
AB = A′B′,
∠A =∠A′,
AC =A′C′ ,
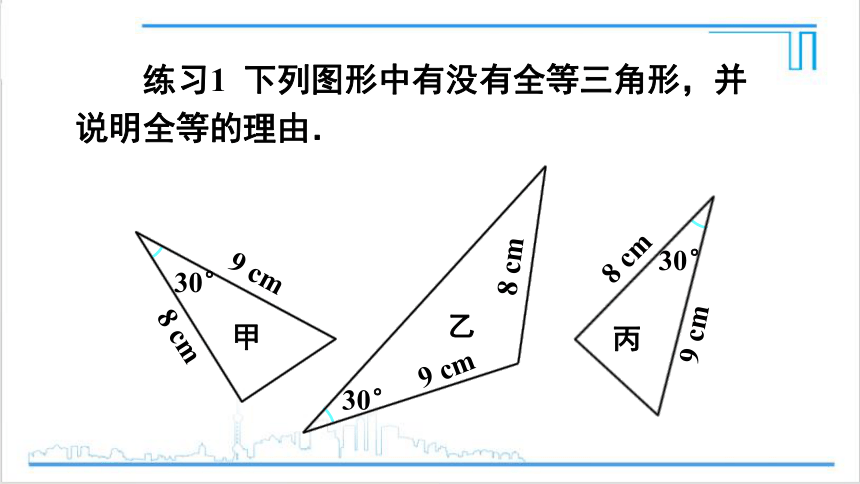
练习1 下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
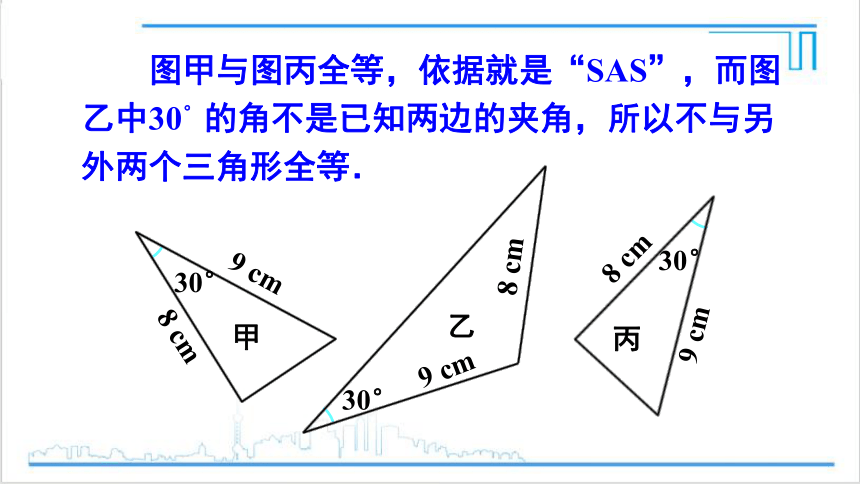
图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.
练习2 ①下列条件中,能用SAS判定△ABC≌△DEF的条件是( )
A. AB = DE,∠A =∠D,BC = EF
B. AB = DE,∠B =∠E,BC = EF
C. AB = EF,∠A =∠D,AC = DF
D. BC = EF,∠C =∠F,AB = DF
B
练习2 ②已知△ABC中,AB = BC ≠ AC,作与△ABC只有一条公共边,且与△ABC 全等的三角形,这样的三角形一共能作出_____个.
7
问题2 某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
“SAS”判定方法的应用
知识点2
利用今天所学“边角边”知识,带黑色的那块.因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
例 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和B. 连接AC并延长到点D,使CD =CA,连接BC 并延长到点E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?
A
B
C
D
E
1
2
AC = DC(已知),
∠1 =∠2 (对顶角相等),
BC =EC(已知) ,
证明:在△ABC 和△DEC 中,
∴ △ABC ≌△DEC(SAS).
∴ AB =DE
(全等三角形的对应边相等).
A
B
C
D
E
1
2
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
问题3 两边一角分别相等包括“两边夹角”和“两边及其中一边的对角”分别相等两种情况,前面已探索出“SAS”判定三角形全等的方法,那么由“SSA”的条件能判定两个三角形全等吗?
A
B
C
D
探索“SSA”能否识别两三角形全等
知识点3
画△ABC 和△DEF,使∠B =∠E =30°, AB =DE=5 cm ,AC =DF =3 cm .观察所得的两个三角形是否全等?
两边和其中一边的对角对应相等这三个条件无法唯一确定三角形的形状,所以不能保证两个三角形全等.因此,△ABC 和△DEF 不一定全等.
练习1 如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地.此时C,D到B的距离相等吗?为什么?
相等,根据边角边定理,△BAD≌△BAC,
∴BD = BC.
【课本P39 练习 第1题】
证明:∵BE = CF ,
∴BE + EF = CF + EF,
即BF = CE,
又AB = DC,∠B =∠C,
∴△ABF≌△DCE,
∴∠A =∠D.
练习2 如图,点E,F在BC上,BE = CF,AB = DC,∠B =∠C.求证∠A =∠D.
【课本P39 练习 第2题】
练习3 如图,在四边形ABCD中,AD∥BC,AD = BC,你能得出AB = CD吗?若能,试说明理由.
A
B
C
D
解:连接AC.
∵AD∥BC,
∴∠DAC=∠BCA.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS).
∴AB = CD.
A
B
C
D
随堂演练
1.下列命题错误的是( )
A.周长相等的两个等边三角形全等
B.两条直角边对应相等的两个直角三角形全等
C.有两条边对应相等的两个等腰三角形不一定全等
D.有两条边和一个角对应相等的两个三角形全等
D
基础巩固
2.如图,AB = AC,若想用“SAS”判定△ABD≌△ACE,则需补充一个条件_________.
AD = AE
3.已知:如图AB = AC,AD = AE,∠BAC =∠DAE,求证: △ABD≌△ACE.
综合应用
证明:∵∠BAC =∠DAE,∴∠BAC+∠CAD =∠DAE +∠CAD,即∠BAD =∠CAE,
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
4. 小明做了一个如图所示的风筝,测得DE = DF,EH = FH,由此你能推出哪些正确结论 并说明理由.
拓展延伸
解:结论:(1)DH平分∠EDF和∠EHF.(2)DH垂直平分EF.
理由:(1)在△EDH和△FDH中,
∴△EDH≌△FDH(SSS).
∴∠EDH =∠FDH,∠EHD =∠FHD.
即DH平分∠EDF和∠EHF.
解:理由:(2)由(1)知,在△EOD和△FOD中,
∴△EOD≌△FOD(SAS).
∴EO = OF,∠EOD =∠FOD =90°,
∴DH 垂直平分EF.
课堂小结
A′
D
E
B′
C′
归纳概括“SAS”判定方法:
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
12.2 三角形全等的判定
第2课时用“SAS”判定三角形全等
R·八年级上册
新课导入
上一节课,我们探究了三条边对应相等的两个三角形全等. 如果两个三角形有两条边和一个角分别对应相等,这两个三角形会全等吗?
——这就是本节课我们要探讨的课题.
学习目标:
1.能说出“边角边”判定定理.
2.会用“边角边”定理证明两个三角形全等.
推进新课
问题1 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′ =AB,∠A′=∠A,C′A′= CA(即两边和它们的夹角分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
边角边的判定方法
知识点1
探究
A′
D
E
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1) 画∠DA′E =∠A;
(2)在射线A′D上截取
A′B′=AB,在射线
A′E上截取A′C′=AC;
(3)连接B′C′.
B′
C′
几何语言:
在△ABC 和△ A′B′ C′中,
∴ △ABC ≌△ A′B′ C′(SAS).
归纳概括“SAS”判定方法:
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).
AB = A′B′,
∠A =∠A′,
AC =A′C′ ,
练习1 下列图形中有没有全等三角形,并说明全等的理由.
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
图甲与图丙全等,依据就是“SAS”,而图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等.
练习2 ①下列条件中,能用SAS判定△ABC≌△DEF的条件是( )
A. AB = DE,∠A =∠D,BC = EF
B. AB = DE,∠B =∠E,BC = EF
C. AB = EF,∠A =∠D,AC = DF
D. BC = EF,∠C =∠F,AB = DF
B
练习2 ②已知△ABC中,AB = BC ≠ AC,作与△ABC只有一条公共边,且与△ABC 全等的三角形,这样的三角形一共能作出_____个.
7
问题2 某同学不小心把一块三角形的玻璃从两个顶点处打碎成两块(如图),现要到玻璃店去配一块完全一样的玻璃.请问如果只准带一块碎片,应该带哪一块去,能试着说明理由吗?
“SAS”判定方法的应用
知识点2
利用今天所学“边角边”知识,带黑色的那块.因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
例 如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和B. 连接AC并延长到点D,使CD =CA,连接BC 并延长到点E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?
A
B
C
D
E
1
2
AC = DC(已知),
∠1 =∠2 (对顶角相等),
BC =EC(已知) ,
证明:在△ABC 和△DEC 中,
∴ △ABC ≌△DEC(SAS).
∴ AB =DE
(全等三角形的对应边相等).
A
B
C
D
E
1
2
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
问题3 两边一角分别相等包括“两边夹角”和“两边及其中一边的对角”分别相等两种情况,前面已探索出“SAS”判定三角形全等的方法,那么由“SSA”的条件能判定两个三角形全等吗?
A
B
C
D
探索“SSA”能否识别两三角形全等
知识点3
画△ABC 和△DEF,使∠B =∠E =30°, AB =DE=5 cm ,AC =DF =3 cm .观察所得的两个三角形是否全等?
两边和其中一边的对角对应相等这三个条件无法唯一确定三角形的形状,所以不能保证两个三角形全等.因此,△ABC 和△DEF 不一定全等.
练习1 如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地.此时C,D到B的距离相等吗?为什么?
相等,根据边角边定理,△BAD≌△BAC,
∴BD = BC.
【课本P39 练习 第1题】
证明:∵BE = CF ,
∴BE + EF = CF + EF,
即BF = CE,
又AB = DC,∠B =∠C,
∴△ABF≌△DCE,
∴∠A =∠D.
练习2 如图,点E,F在BC上,BE = CF,AB = DC,∠B =∠C.求证∠A =∠D.
【课本P39 练习 第2题】
练习3 如图,在四边形ABCD中,AD∥BC,AD = BC,你能得出AB = CD吗?若能,试说明理由.
A
B
C
D
解:连接AC.
∵AD∥BC,
∴∠DAC=∠BCA.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS).
∴AB = CD.
A
B
C
D
随堂演练
1.下列命题错误的是( )
A.周长相等的两个等边三角形全等
B.两条直角边对应相等的两个直角三角形全等
C.有两条边对应相等的两个等腰三角形不一定全等
D.有两条边和一个角对应相等的两个三角形全等
D
基础巩固
2.如图,AB = AC,若想用“SAS”判定△ABD≌△ACE,则需补充一个条件_________.
AD = AE
3.已知:如图AB = AC,AD = AE,∠BAC =∠DAE,求证: △ABD≌△ACE.
综合应用
证明:∵∠BAC =∠DAE,∴∠BAC+∠CAD =∠DAE +∠CAD,即∠BAD =∠CAE,
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
4. 小明做了一个如图所示的风筝,测得DE = DF,EH = FH,由此你能推出哪些正确结论 并说明理由.
拓展延伸
解:结论:(1)DH平分∠EDF和∠EHF.(2)DH垂直平分EF.
理由:(1)在△EDH和△FDH中,
∴△EDH≌△FDH(SSS).
∴∠EDH =∠FDH,∠EHD =∠FHD.
即DH平分∠EDF和∠EHF.
解:理由:(2)由(1)知,在△EOD和△FOD中,
∴△EOD≌△FOD(SAS).
∴EO = OF,∠EOD =∠FOD =90°,
∴DH 垂直平分EF.
课堂小结
A′
D
E
B′
C′
归纳概括“SAS”判定方法:
两边和它们的夹角分别相等的两个三角形全等(可简写成“边角边”或“SAS ”).
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
