【高效备课】人教版八(上) 12.2 三角形全等的判定 第3课时 用“ASA”或“AAS‘判定三角形全等 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 12.2 三角形全等的判定 第3课时 用“ASA”或“AAS‘判定三角形全等 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 747.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:39 | ||
图片预览





文档简介
(共27张PPT)
12.2 三角形全等的判定
第3课时用“ASA”或“AAS”判定三角形全等
R·八年级上册
新课导入
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来形状大小相同的三角形硬纸板吗?下面我们带着这个问题学习判定三角形全等的两个重要方法.
学习目标:
1.能叙述出“角边角”定理.
2.能运用“角边角”定理解决简单的推理证明
问题.
推进新课
问题1 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′ =AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
探究“ASA”判定方法
知识点1
探究
D
E
A′
B′
C′
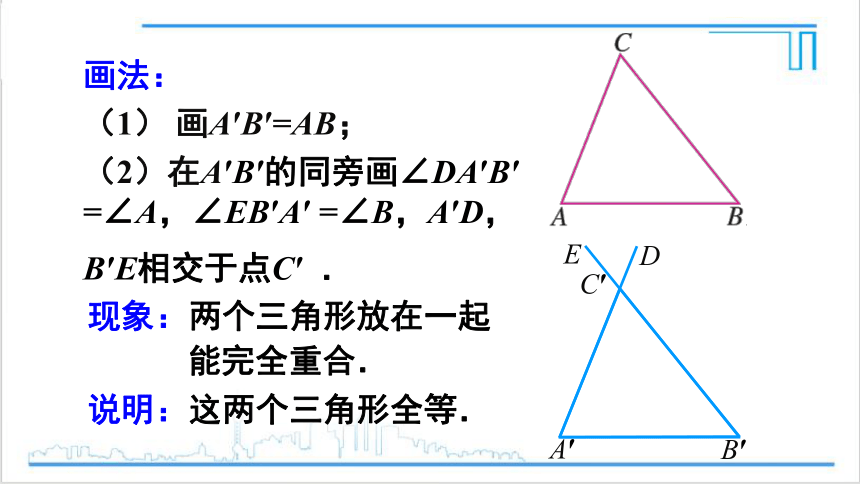
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1) 画A′B′=AB;
(2)在A′B′的同旁画∠DA′B′ =∠A,∠EB′A′ =∠B,A′D,B′E相交于点C′ .
几何语言:
在△ABC 和△ A′B′ C′ 中,
∴△ABC ≌△ A′B′ C′(ASA).
归纳概括“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
∠A =∠A′,
AB = A′B′,
∠B =∠B′,
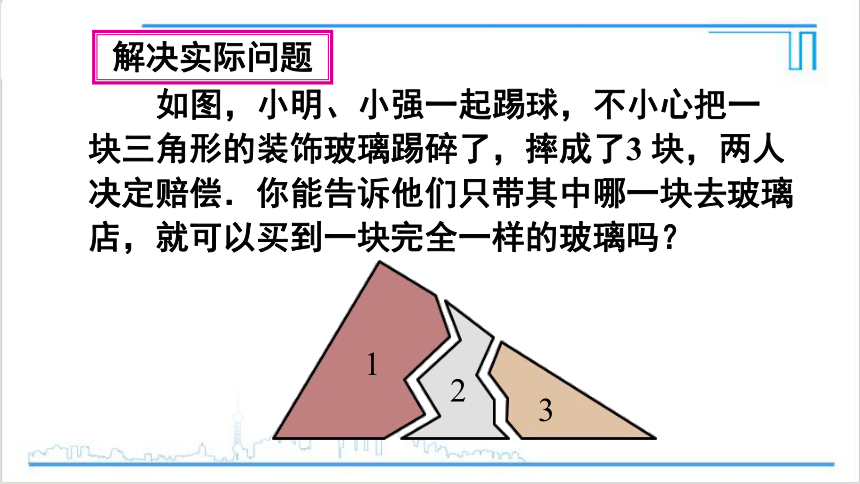
解决实际问题
如图,小明、小强一起踢球,不小心把一 块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?
3
2
1
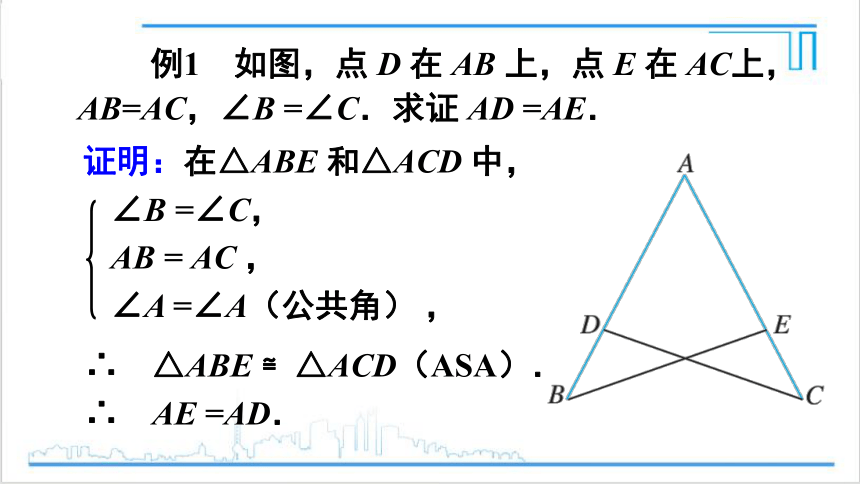
证明:在△ABE 和△ACD 中,
∴ △ABE ≌△ACD(ASA).
∴ AE =AD.
∠B =∠C,
AB = AC ,
∠A =∠A(公共角) ,
例1 如图,点 D 在 AB 上,点 E 在 AC上,AB=AC,∠B =∠C.求证 AD =AE.
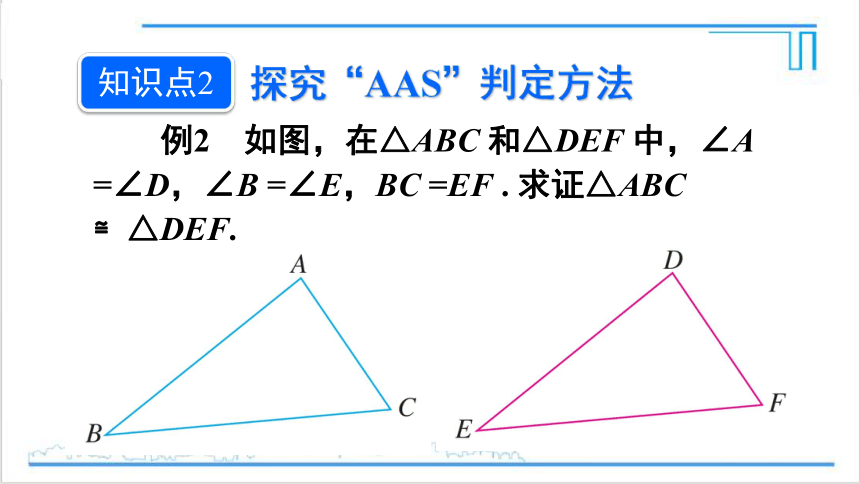
例2 如图,在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF . 求证△ABC ≌△DEF.
探究“AAS”判定方法
知识点2
证明:在△ABC 中, ∠A +∠B +∠C =180°,
∴∠C = 180°-∠A-∠B.
同理∠F =180°-∠D -∠E.
又 ∠A =∠D, ∠B =∠E,
∴∠C = ∠F .
在△ABC 和△DEF 中,
∴△ABC ≌△DEF(ASA).
∠B =∠E,
BC = EF ,
∠C =∠F ,
归纳概括“AAS”判定方法:
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写为“角角边”或“AAS”).
也就是说,三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了.
证明:∵ ∠DAB =∠EAC,
∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,
∴ ∠D =∠E =90°.
在△ADC 和△AEB 中,
A
B
C
D
E
问题2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB =∠EAC.求证:AB =AC.
A
B
C
D
E
问题2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB =∠EAC.求证:AB =AC.
∠DAC =∠EAB,
∠D =∠E,
CD =BE,
∴ △ADC ≌△AEB(AAS).
∴ AB =AC.
证明:
问题3 如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
A
B
C
D
E
F
证明:∵ AD∥CB ,
∴ ∠A =∠C.
∵ AE =CF ,
∴ AF =CE.
在△ADF 和△CBE 中,
问题3 如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
A
B
C
D
E
F
∠A =∠C,
∠D =∠B ,
AF =CE ,
∴ △ADF ≌△CBE(AAS).
∴ DF =BE.
证明:
变式 若将条件 “∠B =∠D”变为“DF∥BE”,那么原结论还成立吗?若成立,请证明;若不成立,请说明理由.
A
B
C
D
E
F
练习1 如图,EA⊥AB,DB⊥AB,∠ACE =∠BDC,AE =BC,试判断CE与CD的关系.
∴△ACE ≌△BDC(AAS).
∠ACE =∠BDC,
∠A =∠B,
AE =BC,
解:∵EA⊥AB,DB⊥AB,
∴∠A =∠B =90°,在△ACE和△BDC中,
∴CE =CD .
练习2 判断.
a.有两条边和一个角对应相等的两个三角形全等. ( )
b.有两个角和一条边对应相等的两个三角形全等. ( )
×
√
随堂演练
1.如图,已知AB = DC,AD = BC,E、F是DB上的两点且BF = DE.若∠AEB = 120°,∠ADB = 30°,则∠BCF =( )
A.150° B.40°
C.80° D.90°
基础巩固
D
2. 如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2. 求证AB=AD.
【课本P41 练习 第1题】
【课本P41 练习 第2题】
3.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A, C在一条直线上,这时测得DE的长就是AB的长. 为什么?
【课本P41 练习 第2题】
4.已知:如图,∠ABC = ∠DEF,AB = DE,要证明△ABC≌△DEF,
(1)若以“SAS”为依据,还须添加的一个条件为____________.
(2)若以“ASA”为依据,还须添加的一个条件为_____________.
(3)若以“AAS”为依据,还须添加的一个条件为_____________.
BC = EF
综合应用
∠A =∠D
∠ACB =∠F
5.如图,点 E、F 在BD上,且 AB = CD,BF = DE,AE = CF,求证:AC 与 BD 互相平分.
拓展延伸
证明:∵BF = DE,
∴BF-EF = DE-EF,即BE = DF.
在△ABE和△CDF中,
∴△ABE≌△CDF. ∴∠B =∠D.
∴AB∥CD. ∴∠BAO =∠DCO.
在△ABO和△CDO中,
∴△ABO≌△CDO,
∴BO = DO,AO = CO,即AC与BD互相平分.
课堂小结
D
E
A′
B′
C′
两角和它们的夹边分别相等的两个三角形全等(简称为“角边角”或“ASA”).
两角分别相等且其中一组等角的对边相等的两个三角形全等(简称为“角角边”或“AAS”).
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
12.2 三角形全等的判定
第3课时用“ASA”或“AAS”判定三角形全等
R·八年级上册
新课导入
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来形状大小相同的三角形硬纸板吗?下面我们带着这个问题学习判定三角形全等的两个重要方法.
学习目标:
1.能叙述出“角边角”定理.
2.能运用“角边角”定理解决简单的推理证明
问题.
推进新课
问题1 先任意画出一个△ABC,再画一个△A′B′C′,使A′B′ =AB,∠A′=∠A,∠B′=∠B(即两角和它们的夹边分别相等).把画好的△A′B′C′剪下来,放到△ABC 上,它们全等吗?
探究“ASA”判定方法
知识点1
探究
D
E
A′
B′
C′
现象:两个三角形放在一起
能完全重合.
说明:这两个三角形全等.
画法:
(1) 画A′B′=AB;
(2)在A′B′的同旁画∠DA′B′ =∠A,∠EB′A′ =∠B,A′D,B′E相交于点C′ .
几何语言:
在△ABC 和△ A′B′ C′ 中,
∴△ABC ≌△ A′B′ C′(ASA).
归纳概括“ASA”判定方法:
两角和它们的夹边分别相等的两个三角形全等(简写为“角边角”或“ASA”).
∠A =∠A′,
AB = A′B′,
∠B =∠B′,
解决实际问题
如图,小明、小强一起踢球,不小心把一 块三角形的装饰玻璃踢碎了,摔成了3 块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?
3
2
1
证明:在△ABE 和△ACD 中,
∴ △ABE ≌△ACD(ASA).
∴ AE =AD.
∠B =∠C,
AB = AC ,
∠A =∠A(公共角) ,
例1 如图,点 D 在 AB 上,点 E 在 AC上,AB=AC,∠B =∠C.求证 AD =AE.
例2 如图,在△ABC 和△DEF 中,∠A =∠D,∠B =∠E,BC =EF . 求证△ABC ≌△DEF.
探究“AAS”判定方法
知识点2
证明:在△ABC 中, ∠A +∠B +∠C =180°,
∴∠C = 180°-∠A-∠B.
同理∠F =180°-∠D -∠E.
又 ∠A =∠D, ∠B =∠E,
∴∠C = ∠F .
在△ABC 和△DEF 中,
∴△ABC ≌△DEF(ASA).
∠B =∠E,
BC = EF ,
∠C =∠F ,
归纳概括“AAS”判定方法:
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写为“角角边”或“AAS”).
也就是说,三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了.
证明:∵ ∠DAB =∠EAC,
∴ ∠DAC =∠EAB.
∵ AE⊥BE,AD⊥DC,
∴ ∠D =∠E =90°.
在△ADC 和△AEB 中,
A
B
C
D
E
问题2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB =∠EAC.求证:AB =AC.
A
B
C
D
E
问题2 如图,AE⊥BE,AD⊥DC,CD =BE,∠DAB =∠EAC.求证:AB =AC.
∠DAC =∠EAB,
∠D =∠E,
CD =BE,
∴ △ADC ≌△AEB(AAS).
∴ AB =AC.
证明:
问题3 如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
A
B
C
D
E
F
证明:∵ AD∥CB ,
∴ ∠A =∠C.
∵ AE =CF ,
∴ AF =CE.
在△ADF 和△CBE 中,
问题3 如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
A
B
C
D
E
F
∠A =∠C,
∠D =∠B ,
AF =CE ,
∴ △ADF ≌△CBE(AAS).
∴ DF =BE.
证明:
变式 若将条件 “∠B =∠D”变为“DF∥BE”,那么原结论还成立吗?若成立,请证明;若不成立,请说明理由.
A
B
C
D
E
F
练习1 如图,EA⊥AB,DB⊥AB,∠ACE =∠BDC,AE =BC,试判断CE与CD的关系.
∴△ACE ≌△BDC(AAS).
∠ACE =∠BDC,
∠A =∠B,
AE =BC,
解:∵EA⊥AB,DB⊥AB,
∴∠A =∠B =90°,在△ACE和△BDC中,
∴CE =CD .
练习2 判断.
a.有两条边和一个角对应相等的两个三角形全等. ( )
b.有两个角和一条边对应相等的两个三角形全等. ( )
×
√
随堂演练
1.如图,已知AB = DC,AD = BC,E、F是DB上的两点且BF = DE.若∠AEB = 120°,∠ADB = 30°,则∠BCF =( )
A.150° B.40°
C.80° D.90°
基础巩固
D
2. 如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2. 求证AB=AD.
【课本P41 练习 第1题】
【课本P41 练习 第2题】
3.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A, C在一条直线上,这时测得DE的长就是AB的长. 为什么?
【课本P41 练习 第2题】
4.已知:如图,∠ABC = ∠DEF,AB = DE,要证明△ABC≌△DEF,
(1)若以“SAS”为依据,还须添加的一个条件为____________.
(2)若以“ASA”为依据,还须添加的一个条件为_____________.
(3)若以“AAS”为依据,还须添加的一个条件为_____________.
BC = EF
综合应用
∠A =∠D
∠ACB =∠F
5.如图,点 E、F 在BD上,且 AB = CD,BF = DE,AE = CF,求证:AC 与 BD 互相平分.
拓展延伸
证明:∵BF = DE,
∴BF-EF = DE-EF,即BE = DF.
在△ABE和△CDF中,
∴△ABE≌△CDF. ∴∠B =∠D.
∴AB∥CD. ∴∠BAO =∠DCO.
在△ABO和△CDO中,
∴△ABO≌△CDO,
∴BO = DO,AO = CO,即AC与BD互相平分.
课堂小结
D
E
A′
B′
C′
两角和它们的夹边分别相等的两个三角形全等(简称为“角边角”或“ASA”).
两角分别相等且其中一组等角的对边相等的两个三角形全等(简称为“角角边”或“AAS”).
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
