【高效备课】人教版八(上) 13.1 轴对称 13.1.2 线段的垂直平分线的性质 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 13.1 轴对称 13.1.2 线段的垂直平分线的性质 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 301.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:39 | ||
图片预览






文档简介
(共33张PPT)
13.1.2 线段的垂直平分线的性质
R·八年级上册
新课导入
导入课题
前面我们已经学习了轴对称图形和两个图形成轴对称的意义和性质,这节课我们一起运用轴对称来探索线段垂直平分线的性质和判定.
学习目标
(1)能叙述出线段垂直平分线的性质.
(2)能运用线段垂直平分线的性质解决有关问题.
(3)能说出线段垂直平分线的判定方法.
推进新课
知识点1
探索并证明线段垂直平分线的性质
探究
如图,直线 l 垂直平分线段 AB,P1,P2,P3,…是 l 上的点,分别量一量点 P1,P2,P3,… 到点 A 与点 B 的距离,你有什么发现?
A
B
l
P1
P2
P3
你能用不同的方法验证这一结论吗?
相等.
请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗?
探究
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
B
l
P1
P2
P3
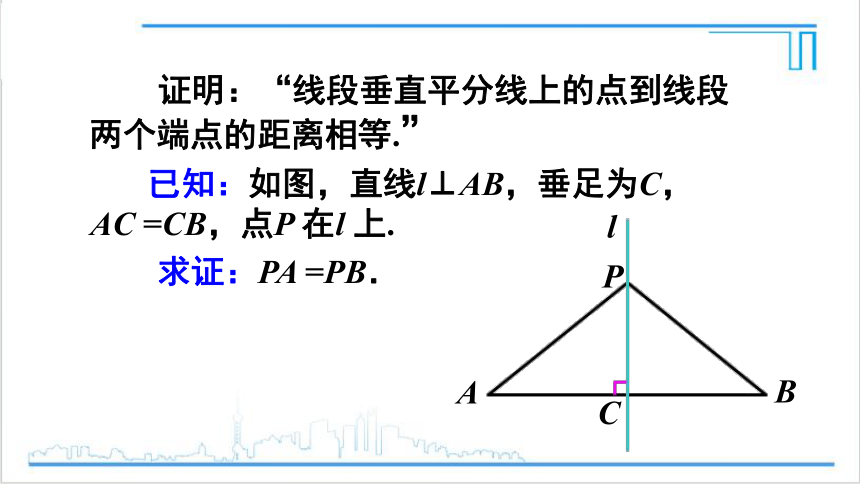
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:“线段垂直平分线上的点到线段两个端点的距离相等.”
A
B
P
C
l
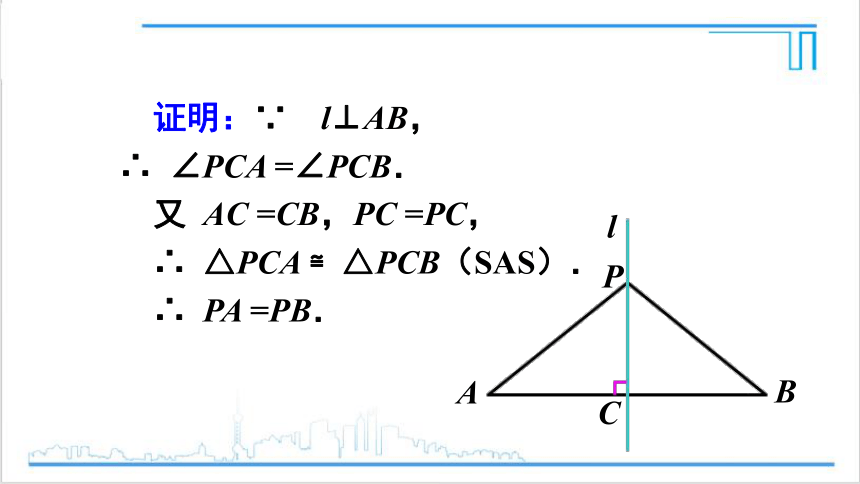
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
A
B
P
C
l
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
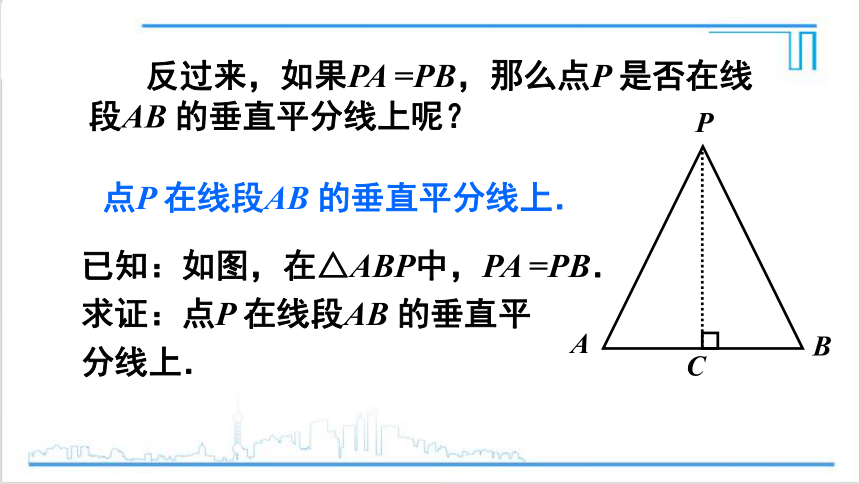
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,在△ABP中,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
P
A
B
C
P
A
B
C
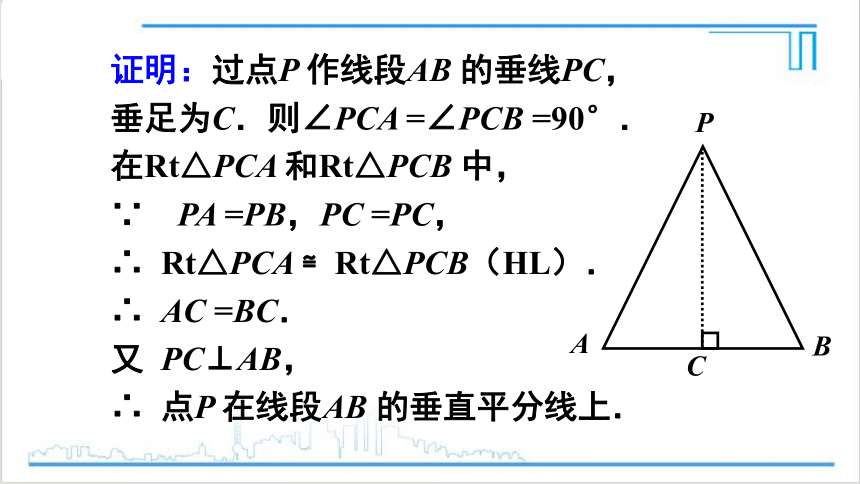
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
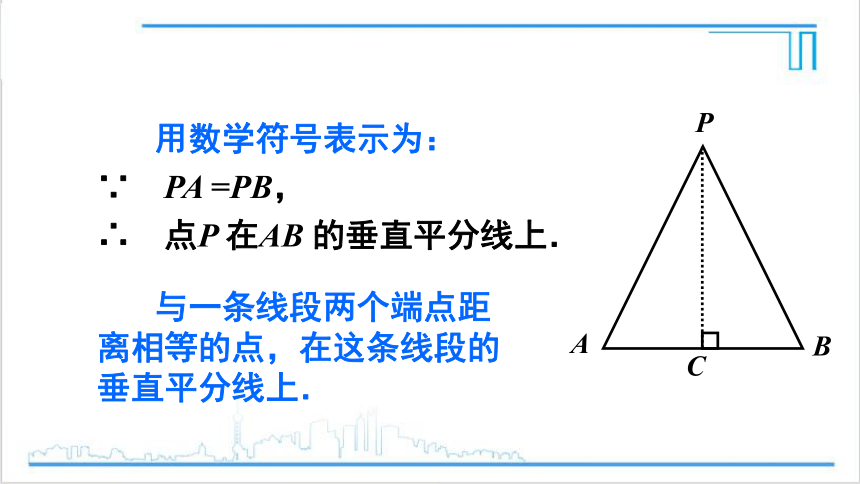
用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
P
A
B
C
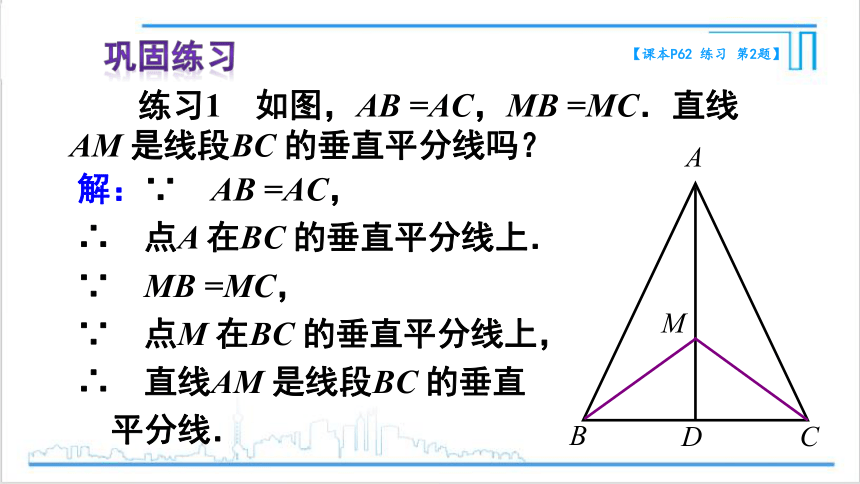
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线上.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.
练习1 如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
巩固练习
【课本P62 练习 第2题】
练习2 如图,在△ABC 中,BC =8,AB 的中垂线交BC 于D,AC 的中垂线交BC 与E,则△ADE 的周长等于______.
8
A
B
C
D
E
练习3 到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点
B.三边垂直平分线的交点
C.三边高线的交点
D.没有这样的点
B
知识点2
例1 尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C(如图).
求作:AB的垂线,使它经过点C.
经过已知直线外一点作这条直线的垂线
A
B
C
作法:(1)任意取一点K ,使点K和点C 在AB 的两旁.
(3)分别以点D和点E为圆心,大
于 DE的长为半径作弧,两弧
相交于点F .
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E .
(4)作直线CF.
直线CF 就是所求作的垂线.
C
A
B
D
E
F
K
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
练习4 如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
A
B
C
D
E
巩固练习
【课本P62 练习 第1题】
A
B
C
D
E
∴ AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
∵ 点C 在AE 的垂直平
分线上,
∴ AC =CE.
知识点3
作线段的垂直平分线
例2 如图,点A 和点B 关于某条直线成轴对称,你能作出这条直线吗?
A
B
怎样作线段AB 的垂直平分线呢?
这种作法的依据是什么?
这种作图方法还有哪些作用?
确定线段的中点.
作法:如图.
(1)分别以点A,B 为圆心,以大于 AB的长为半径作弧,两弧相交于C,D 两点;
(2)作直线CD.
CD 就是所求作的直线.
A
B
C
D
如果两个图形成轴对称,怎样作出图形的对称轴?
如果两个图形成轴对称,其对称轴是任何一组对应点所连线段的垂直平分线.因此,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
如图中的五角星,请作出它的一条对称轴.
你能作出这个五角星的其他对称轴吗?它共有几条对称轴?
五角星的对称轴有什么特点?
巩固练习
练习5 作出下列图形的一条对称轴,和同桌比较一下,你们作出的对称轴一样吗?
练习6 如图,角是轴对称图形吗?如果是,它的对称轴是什么?
练习7 如图,与图形A 成轴对称的是哪个图形?画出它们的对称轴.
A
B
C
D
随堂演练
基础巩固
1.如图,直线CD是线段AB的垂直平分线,M是直线CD上的一点.已知线段MA=12cm,则线段MB的长为_____cm.
12
2. 在△ABC中,AB的中垂线与AC边所在直线相交所得的锐角为50°,则∠A的度数为( )
A.50° B.40°
C.40°或140° D.40°或50°
C
3.画出下列图形的对称轴(有几条对称轴就画出几条,不要遗漏).
综合应用
4.如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在点C′处BC′交AD于E;
(1)若∠DBC=22.5°,则在不添加辅助线的情况下,图中45°的角(虚线也视为角的边)有多少个?
(2)你认为图中有多少组全等三角形,并把他们写下来.
解:(1)5个.
(2)4组,
△BCD≌△BC′D,△ABE≌△C′DB,△ABD≌△CDB,△ABD≌△C′DB.
拓展延伸
5.电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?在图上标出它的位置.
解:如图所示,两条高速公路相交的角的角平分线和AB的垂直平分线的交点P1与P2点.
课堂小结
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
13.1.2 线段的垂直平分线的性质
R·八年级上册
新课导入
导入课题
前面我们已经学习了轴对称图形和两个图形成轴对称的意义和性质,这节课我们一起运用轴对称来探索线段垂直平分线的性质和判定.
学习目标
(1)能叙述出线段垂直平分线的性质.
(2)能运用线段垂直平分线的性质解决有关问题.
(3)能说出线段垂直平分线的判定方法.
推进新课
知识点1
探索并证明线段垂直平分线的性质
探究
如图,直线 l 垂直平分线段 AB,P1,P2,P3,…是 l 上的点,分别量一量点 P1,P2,P3,… 到点 A 与点 B 的距离,你有什么发现?
A
B
l
P1
P2
P3
你能用不同的方法验证这一结论吗?
相等.
请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗?
探究
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
B
l
P1
P2
P3
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:“线段垂直平分线上的点到线段两个端点的距离相等.”
A
B
P
C
l
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
A
B
P
C
l
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,在△ABP中,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.
P
A
B
C
P
A
B
C
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
P
A
B
C
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线上.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.
练习1 如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
巩固练习
【课本P62 练习 第2题】
练习2 如图,在△ABC 中,BC =8,AB 的中垂线交BC 于D,AC 的中垂线交BC 与E,则△ADE 的周长等于______.
8
A
B
C
D
E
练习3 到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点
B.三边垂直平分线的交点
C.三边高线的交点
D.没有这样的点
B
知识点2
例1 尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C(如图).
求作:AB的垂线,使它经过点C.
经过已知直线外一点作这条直线的垂线
A
B
C
作法:(1)任意取一点K ,使点K和点C 在AB 的两旁.
(3)分别以点D和点E为圆心,大
于 DE的长为半径作弧,两弧
相交于点F .
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E .
(4)作直线CF.
直线CF 就是所求作的垂线.
C
A
B
D
E
F
K
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
练习4 如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
A
B
C
D
E
巩固练习
【课本P62 练习 第1题】
A
B
C
D
E
∴ AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
∵ 点C 在AE 的垂直平
分线上,
∴ AC =CE.
知识点3
作线段的垂直平分线
例2 如图,点A 和点B 关于某条直线成轴对称,你能作出这条直线吗?
A
B
怎样作线段AB 的垂直平分线呢?
这种作法的依据是什么?
这种作图方法还有哪些作用?
确定线段的中点.
作法:如图.
(1)分别以点A,B 为圆心,以大于 AB的长为半径作弧,两弧相交于C,D 两点;
(2)作直线CD.
CD 就是所求作的直线.
A
B
C
D
如果两个图形成轴对称,怎样作出图形的对称轴?
如果两个图形成轴对称,其对称轴是任何一组对应点所连线段的垂直平分线.因此,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
如图中的五角星,请作出它的一条对称轴.
你能作出这个五角星的其他对称轴吗?它共有几条对称轴?
五角星的对称轴有什么特点?
巩固练习
练习5 作出下列图形的一条对称轴,和同桌比较一下,你们作出的对称轴一样吗?
练习6 如图,角是轴对称图形吗?如果是,它的对称轴是什么?
练习7 如图,与图形A 成轴对称的是哪个图形?画出它们的对称轴.
A
B
C
D
随堂演练
基础巩固
1.如图,直线CD是线段AB的垂直平分线,M是直线CD上的一点.已知线段MA=12cm,则线段MB的长为_____cm.
12
2. 在△ABC中,AB的中垂线与AC边所在直线相交所得的锐角为50°,则∠A的度数为( )
A.50° B.40°
C.40°或140° D.40°或50°
C
3.画出下列图形的对称轴(有几条对称轴就画出几条,不要遗漏).
综合应用
4.如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在点C′处BC′交AD于E;
(1)若∠DBC=22.5°,则在不添加辅助线的情况下,图中45°的角(虚线也视为角的边)有多少个?
(2)你认为图中有多少组全等三角形,并把他们写下来.
解:(1)5个.
(2)4组,
△BCD≌△BC′D,△ABE≌△C′DB,△ABD≌△CDB,△ABD≌△C′DB.
拓展延伸
5.电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?在图上标出它的位置.
解:如图所示,两条高速公路相交的角的角平分线和AB的垂直平分线的交点P1与P2点.
课堂小结
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
