【高效备课】人教版八(上) 15.2 分式的运算 15.2.3 整数指数幂 第1课时 整数指数幂 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 15.2 分式的运算 15.2.3 整数指数幂 第1课时 整数指数幂 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 322.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:39 | ||
图片预览






文档简介
(共19张PPT)
15.2.3 整数指数幂
第1课时 整数指数幂
R·八年级上册
新课导入
同学们还记得正整数指数幂的运算性质吗?由am÷an=am-n,当m<n时,底数a的指数(m-n)是负整数,那么它表示什么呢?
学习目标:
1.知道负整数指数幂的意义及表示法.
2.能运用分式的有关知识推导整数指数幂的 意义.
推进新课
整数指数幂
知识点1
将正整数指数幂的运算性质中指数的取值范围由“正整数”扩大到“整数”,这些性质还适用吗?
问题1 你们还记得正整数指数幂的意义吗?正整数指数幂有哪些运算性质呢?
(1)根据分式的约分,当 a≠0 时,如何计算 ?
问题2 am 中指数m 可以是负整数吗?如果可以,那么负整数指数幂am 表示什么?
(2)如果把正整数指数幂的运算性质
(a≠0,m,n 是正整数,m >n)中的条件m >n 去
掉,即假设这个性质对于像 情形也能使用,
如何计算?
数学中规定:当n 是正整数时,
这就是说,a-n(a≠0)是an 的倒数.
试说说当m分别是正整数、0、负整数时,am各表示什么意义?
当m是正整数时, am表示m个a相乘.当m是0时,a0表示一个数的n次方除以这个数的n次方,所以特别规定,任何除0以外的实数的0次方都是1.
当m是负整数时, am表示|m|个 相乘.
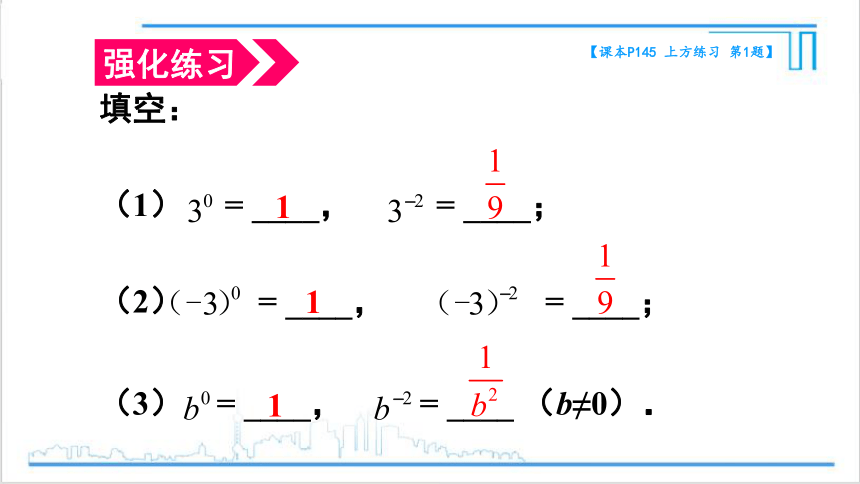
填空:
(1) = ____, = ____;
(2) = ____, = ____;
(3) = ____, = ____ (b≠0).
强化练习
1
1
1
【课本P145 上方练习 第1题】
整数指数幂的性质
知识点2
(m,n 是正整数)这条性质能否推广到m,n 是任意整数的情形?
问题3 引入负整数指数和0指数后,
问题4 类似地,你可以用负整数指数幂或0 指数幂对其他正整数指数幂的运算性质进行试验,这些性质在整数范围内是否还适用?
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
(4) (m,n 是整数);
(5) (n 是整数).
总结:
问题5 能否将整数指数幂的5条性质进行适当合并?
根据整数指数幂的运算性质,当m,n为整数时,
, ,因此,
,即同底数幂的除法 可
以转化为同底数幂的乘法 .特别地,
所以,
即商的乘方 可以转化为积的乘方
这样,整数指数幂的运算性质可以归结为:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数).
强化练习
计算:
【课本P145 上方练习 第2题】
随堂演练
1.填空:
(1)30= ,3-2= ,(-3)0= ,(-3)-2= .
(2)3-3= ,(-3)-3= .
(3) = , = , = .
2.若m,n为正整数,则下列各式错误的是( )
3.下列计算正确的是( )
4.计算.
5.若 ,试求 的值.
课堂小结
数学中规定:当n 是正整数时,
这就是说,a-n(a≠0)是an 的倒数.
整数指数幂的运算性质可以归结为:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数).
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
15.2.3 整数指数幂
第1课时 整数指数幂
R·八年级上册
新课导入
同学们还记得正整数指数幂的运算性质吗?由am÷an=am-n,当m<n时,底数a的指数(m-n)是负整数,那么它表示什么呢?
学习目标:
1.知道负整数指数幂的意义及表示法.
2.能运用分式的有关知识推导整数指数幂的 意义.
推进新课
整数指数幂
知识点1
将正整数指数幂的运算性质中指数的取值范围由“正整数”扩大到“整数”,这些性质还适用吗?
问题1 你们还记得正整数指数幂的意义吗?正整数指数幂有哪些运算性质呢?
(1)根据分式的约分,当 a≠0 时,如何计算 ?
问题2 am 中指数m 可以是负整数吗?如果可以,那么负整数指数幂am 表示什么?
(2)如果把正整数指数幂的运算性质
(a≠0,m,n 是正整数,m >n)中的条件m >n 去
掉,即假设这个性质对于像 情形也能使用,
如何计算?
数学中规定:当n 是正整数时,
这就是说,a-n(a≠0)是an 的倒数.
试说说当m分别是正整数、0、负整数时,am各表示什么意义?
当m是正整数时, am表示m个a相乘.当m是0时,a0表示一个数的n次方除以这个数的n次方,所以特别规定,任何除0以外的实数的0次方都是1.
当m是负整数时, am表示|m|个 相乘.
填空:
(1) = ____, = ____;
(2) = ____, = ____;
(3) = ____, = ____ (b≠0).
强化练习
1
1
1
【课本P145 上方练习 第1题】
整数指数幂的性质
知识点2
(m,n 是正整数)这条性质能否推广到m,n 是任意整数的情形?
问题3 引入负整数指数和0指数后,
问题4 类似地,你可以用负整数指数幂或0 指数幂对其他正整数指数幂的运算性质进行试验,这些性质在整数范围内是否还适用?
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
(4) (m,n 是整数);
(5) (n 是整数).
总结:
问题5 能否将整数指数幂的5条性质进行适当合并?
根据整数指数幂的运算性质,当m,n为整数时,
, ,因此,
,即同底数幂的除法 可
以转化为同底数幂的乘法 .特别地,
所以,
即商的乘方 可以转化为积的乘方
这样,整数指数幂的运算性质可以归结为:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数).
强化练习
计算:
【课本P145 上方练习 第2题】
随堂演练
1.填空:
(1)30= ,3-2= ,(-3)0= ,(-3)-2= .
(2)3-3= ,(-3)-3= .
(3) = , = , = .
2.若m,n为正整数,则下列各式错误的是( )
3.下列计算正确的是( )
4.计算.
5.若 ,试求 的值.
课堂小结
数学中规定:当n 是正整数时,
这就是说,a-n(a≠0)是an 的倒数.
整数指数幂的运算性质可以归结为:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数).
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
