【高效备课】人教版八(上) 14.2 乘法公式 14.2.1 平方差公式 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 14.2 乘法公式 14.2.1 平方差公式 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:39 | ||
图片预览







文档简介
(共24张PPT)
14.2 乘法公式
14.2.1 平方差公式
R·八年级上册
某同学在计算98×102时将其变成(100-2)(100+2)并很快得出结果,你知道他运用了什么知识吗?这节课我们一起来探讨上述计算的规律.
新课导入
学习目标
1. 掌握平方差公式的推导及应用.
2. 了解平方差公式的几何意义,体会数形结合
的思想方法.
推进新课
探究平方差公式
知识点1
探究
计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x-1)= ;
(2)(m+2)(m-2)= ;
(3)(2x+1)(2x-1)= .
x2-1
m2-4
4x2-1
相乘的两个多项式有什么共同点?
都是形如a+b的多项式与a-b的多项式相乘.
思考
观察上面的结果,你发现了什么规律?
(1)(x+1)(x-1)= ;
(2)(m+2)(m-2)= ;
(3)(2x+1)(2x-1)= .
x2-1
m2-4
4x2-1
两个数的和与这两个数的差的积,等于这两个数的平方差.
你能将上面发现的规律推导出来吗?
(a+b)(a-b)
=a2-ab+ab-b2
=a2-b2
(a+b)(a-b)=a2-b2
即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做平方差公式.
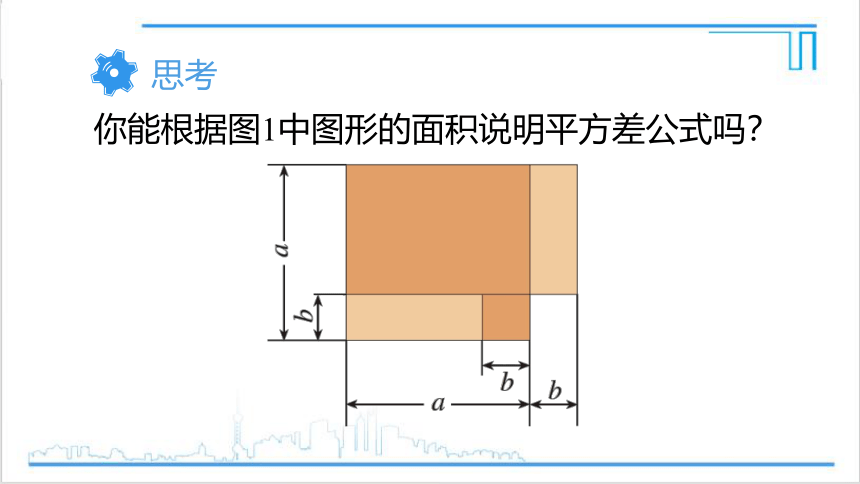
你能根据图1中图形的面积说明平方差公式吗?
思考
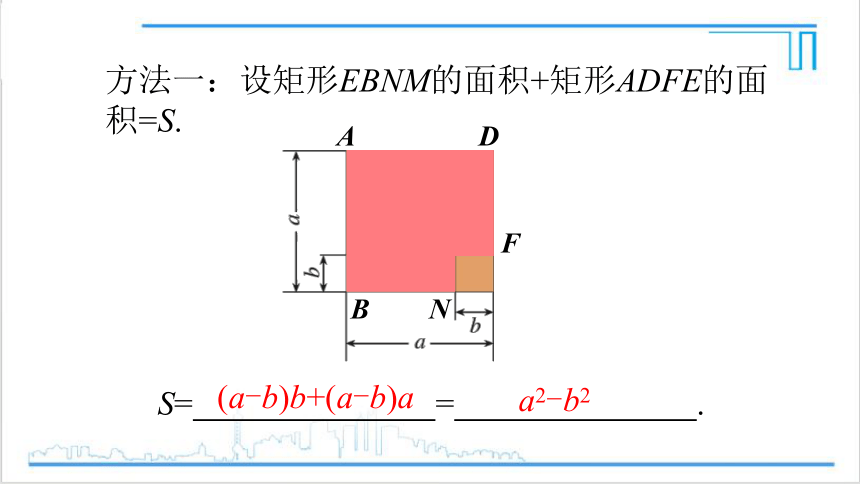
方法一:设矩形EBNM的面积+矩形ADFE的面积=S.
S= = .
A
D
F
E
B
N
M
(a-b)b+(a-b)a
a2-b2
方法二:剪下矩形EBNM拼到FBND的位置,如图.
S=S四边形AEBN = .
A
D(M)
N
E
B
N
M
B
(a-b)(a+b)
平方差公式的应用
知识点2
(1)(3x+2)(3x-2); (2)(-x+2y)(-x-2y).
3x
例 运用平方差公式计算:
(1)中,可以将 看作a,将 看作b,计算结果是 . (2)中,可以将 看作a,将 看作b,计算结果是 .
2
9x2 -4
-x
2y
x2 -4y2
例 计算:
(1)( y+2)( y-2)-( y-1)( y+5);
(2)102×98.
( y-1)( y+5)可以用平方差公式进行运算吗?
不能,不符合平方差公式的条件.
自己动手算一算.
解:(1)( y+2)( y-2)-( y-1)( y+5)
=y2-4-( y2+4y-5)
=1-4y;
(2)102×98
=(100+2)(100-2)
=1002-22
=9996.
下列式子能用平方差公式计算吗
① (-3x+2)(3x-2) ② (b+2a)(2a-b)
③ (-x+2y)(-x-2y) ④ (-x+y)(x-y)
强化练习
不能
不能
能,4a2-b2
能,x2-4y2
随堂演练
1.下列多项式中,可以用平方差公式计算的
是( )
A.(2a-3b)(-2a+3b) B.(-3a+4b)(-4b-3a)
C.(a-b)(b-a) D.(a-b-c)(-a+b+c)
B
解析:(-3a+4b)(-4b-3a)=(-3a+4b)(-3a-4b)
=9a2-16b2
【课本P108 练习 第1题】
2.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2) =x2-2
(2)(-3a-2)(3a-2) =9a2-4
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
4.下列计算结果正确的是( )
A.(x+2)(x-2)=x2-2
B.(x+2)(3x-2)=3x2-4
C.(ab-c)(ab+c)=a2b2-c2
D.(-x-y)(x+y)=x2-y2
C
x2-4
3x2+4x-4
-x2-y2-2xy
5.用简便方法计算:
20152-2014×2016
解:原式=20152-(2015-1)×(2015+1)
=20152-(20152-12)
=1
课堂小结
(a+b)(a-b)=a2-b2
即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做平方差公式.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
14.2 乘法公式
14.2.1 平方差公式
R·八年级上册
某同学在计算98×102时将其变成(100-2)(100+2)并很快得出结果,你知道他运用了什么知识吗?这节课我们一起来探讨上述计算的规律.
新课导入
学习目标
1. 掌握平方差公式的推导及应用.
2. 了解平方差公式的几何意义,体会数形结合
的思想方法.
推进新课
探究平方差公式
知识点1
探究
计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x-1)= ;
(2)(m+2)(m-2)= ;
(3)(2x+1)(2x-1)= .
x2-1
m2-4
4x2-1
相乘的两个多项式有什么共同点?
都是形如a+b的多项式与a-b的多项式相乘.
思考
观察上面的结果,你发现了什么规律?
(1)(x+1)(x-1)= ;
(2)(m+2)(m-2)= ;
(3)(2x+1)(2x-1)= .
x2-1
m2-4
4x2-1
两个数的和与这两个数的差的积,等于这两个数的平方差.
你能将上面发现的规律推导出来吗?
(a+b)(a-b)
=a2-ab+ab-b2
=a2-b2
(a+b)(a-b)=a2-b2
即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做平方差公式.
你能根据图1中图形的面积说明平方差公式吗?
思考
方法一:设矩形EBNM的面积+矩形ADFE的面积=S.
S= = .
A
D
F
E
B
N
M
(a-b)b+(a-b)a
a2-b2
方法二:剪下矩形EBNM拼到FBND的位置,如图.
S=S四边形AEBN = .
A
D(M)
N
E
B
N
M
B
(a-b)(a+b)
平方差公式的应用
知识点2
(1)(3x+2)(3x-2); (2)(-x+2y)(-x-2y).
3x
例 运用平方差公式计算:
(1)中,可以将 看作a,将 看作b,计算结果是 . (2)中,可以将 看作a,将 看作b,计算结果是 .
2
9x2 -4
-x
2y
x2 -4y2
例 计算:
(1)( y+2)( y-2)-( y-1)( y+5);
(2)102×98.
( y-1)( y+5)可以用平方差公式进行运算吗?
不能,不符合平方差公式的条件.
自己动手算一算.
解:(1)( y+2)( y-2)-( y-1)( y+5)
=y2-4-( y2+4y-5)
=1-4y;
(2)102×98
=(100+2)(100-2)
=1002-22
=9996.
下列式子能用平方差公式计算吗
① (-3x+2)(3x-2) ② (b+2a)(2a-b)
③ (-x+2y)(-x-2y) ④ (-x+y)(x-y)
强化练习
不能
不能
能,4a2-b2
能,x2-4y2
随堂演练
1.下列多项式中,可以用平方差公式计算的
是( )
A.(2a-3b)(-2a+3b) B.(-3a+4b)(-4b-3a)
C.(a-b)(b-a) D.(a-b-c)(-a+b+c)
B
解析:(-3a+4b)(-4b-3a)=(-3a+4b)(-3a-4b)
=9a2-16b2
【课本P108 练习 第1题】
2.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2) =x2-2
(2)(-3a-2)(3a-2) =9a2-4
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
(2)51×49
(4)(3x+4)(3x-4) -(2x+3)(3x-2)
4.下列计算结果正确的是( )
A.(x+2)(x-2)=x2-2
B.(x+2)(3x-2)=3x2-4
C.(ab-c)(ab+c)=a2b2-c2
D.(-x-y)(x+y)=x2-y2
C
x2-4
3x2+4x-4
-x2-y2-2xy
5.用简便方法计算:
20152-2014×2016
解:原式=20152-(2015-1)×(2015+1)
=20152-(20152-12)
=1
课堂小结
(a+b)(a-b)=a2-b2
即两个数的和与这两个数的差的积,等于这两个数的平方差.这个公式叫做平方差公式.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
