【高效备课】人教版八(上) 第11章 三角形 复习题11 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 第11章 三角形 复习题11 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 952.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:39 | ||
图片预览




文档简介
(共15张PPT)
复习题11
R·八年级上册
复习巩固
1. 如图,在△ABC 中,AD,AE 分别是边 BC 上的中线和高,AE = 2 cm,S△ABD = 1.5 cm2. 求 BC 和 DC 的长.
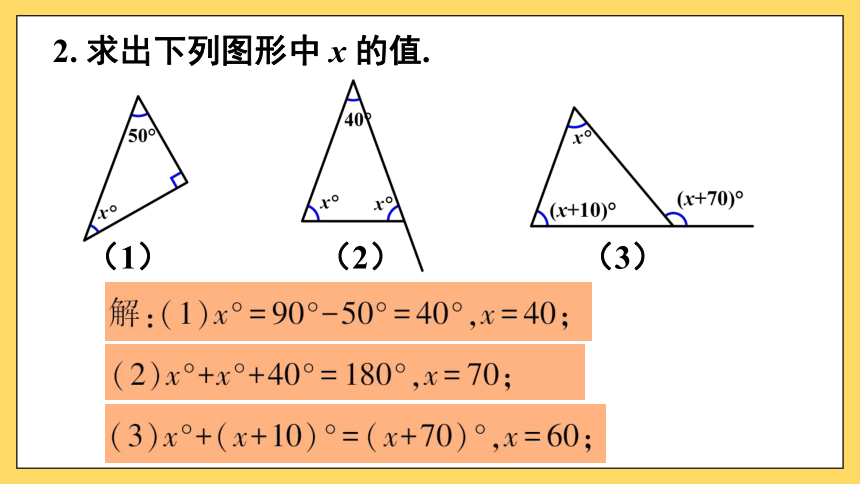
2. 求出下列图形中 x 的值.
(1)
(2)
(3)
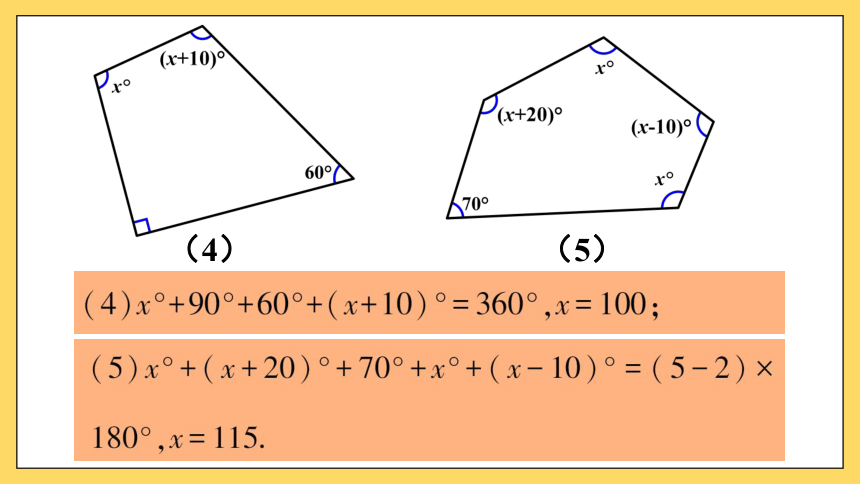
(4)
(5)
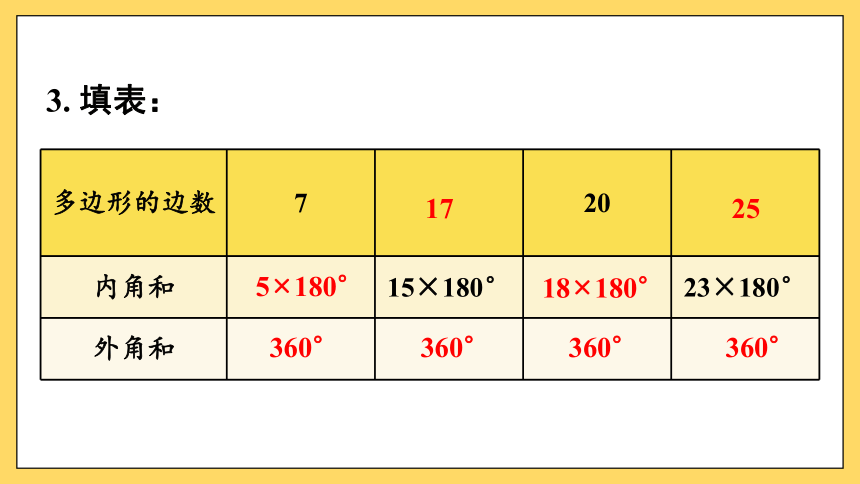
3. 填表:
多边形的边数 7 20
内角和 15×180° 23×180°
外角和
5×180°
360°
17
360°
18×180°
360°
25
360°
4. 从八边形的一个顶点出发,可以作几条对角线?它们将八边形分成几个三角形?这些三角形的内角和与八边形的内角和有什么关系?
5.一个多边形的内角和比四边形的内角和多540°,并且这个多边形的各内角都相等. 这个多边形的每个内角等于多少度?
综合运用
6. 如图,∠B = 42°,∠A+10°= ∠1,∠ACD = 64°.
求证 AB∥CD.
7. 如图,在△ABC 中,∠C = ∠ABC = 2∠A,
BD 是边 AC 上的高,求 ∠DBC 的度数。
8. 如图,在△ABC 中,AD 是高,AE,BF 是角平分线,它们相交于点 O,∠BAC = 50°,∠C = 70°. 求∠DAC 和∠BOA 的度数.
解:如图,∵∠BAC = 50°,∠C=70°,
∴∠ABC = 180°-(∠BAC+∠C )= 180°-(50°+70°) = 60°.
又 AE,BF 分别是 ∠BAC,∠ABC 的平分线,
∴∠1= ∠BAC = ×50°=25°,∠2= ∠ABC = ×60°= 30°.
∴在△AOB中,
∠BOA = 180°-(∠1+∠2)= 180°-( 25°+30°)= 125°.
∵在△ABC中,AD 是高,∴∠ADC = 90°.
又∠C = 70°,
∴∠DAC = 180°-(∠ADC+∠C )=180°-( 90°+70° )= 20°.
9. 如图,填空:
由三角形两边的和大于第三边,得
AB + AD >______________,
PD + CD >______________.
将不等式左边、右边分别相加,得
AB + AD + PD + CD >______________,
即 AB + AC >_______________.
BD
PC
BD + PC
PB + PC
10. 如图,五边形 ABCDE 的内角都相等,DF ⊥ AB.
求 ∠CDF 的度数.
拓广探索
11. 如图,△ABC 的 ∠ABC 和∠ACB 的平分线 BE,CF
相交于点 G. 求证:
(1)∠BGC = 180°- ( ∠ABC + ∠ACB );
(2)∠BGC = 90°+ ∠A.
12. 如图,在四边形 ABCD 中,∠A =∠C = 90°,
BE 平分∠ABC,DF 平分 ∠CDA. 求证 BE // DF.
复习题11
R·八年级上册
复习巩固
1. 如图,在△ABC 中,AD,AE 分别是边 BC 上的中线和高,AE = 2 cm,S△ABD = 1.5 cm2. 求 BC 和 DC 的长.
2. 求出下列图形中 x 的值.
(1)
(2)
(3)
(4)
(5)
3. 填表:
多边形的边数 7 20
内角和 15×180° 23×180°
外角和
5×180°
360°
17
360°
18×180°
360°
25
360°
4. 从八边形的一个顶点出发,可以作几条对角线?它们将八边形分成几个三角形?这些三角形的内角和与八边形的内角和有什么关系?
5.一个多边形的内角和比四边形的内角和多540°,并且这个多边形的各内角都相等. 这个多边形的每个内角等于多少度?
综合运用
6. 如图,∠B = 42°,∠A+10°= ∠1,∠ACD = 64°.
求证 AB∥CD.
7. 如图,在△ABC 中,∠C = ∠ABC = 2∠A,
BD 是边 AC 上的高,求 ∠DBC 的度数。
8. 如图,在△ABC 中,AD 是高,AE,BF 是角平分线,它们相交于点 O,∠BAC = 50°,∠C = 70°. 求∠DAC 和∠BOA 的度数.
解:如图,∵∠BAC = 50°,∠C=70°,
∴∠ABC = 180°-(∠BAC+∠C )= 180°-(50°+70°) = 60°.
又 AE,BF 分别是 ∠BAC,∠ABC 的平分线,
∴∠1= ∠BAC = ×50°=25°,∠2= ∠ABC = ×60°= 30°.
∴在△AOB中,
∠BOA = 180°-(∠1+∠2)= 180°-( 25°+30°)= 125°.
∵在△ABC中,AD 是高,∴∠ADC = 90°.
又∠C = 70°,
∴∠DAC = 180°-(∠ADC+∠C )=180°-( 90°+70° )= 20°.
9. 如图,填空:
由三角形两边的和大于第三边,得
AB + AD >______________,
PD + CD >______________.
将不等式左边、右边分别相加,得
AB + AD + PD + CD >______________,
即 AB + AC >_______________.
BD
PC
BD + PC
PB + PC
10. 如图,五边形 ABCDE 的内角都相等,DF ⊥ AB.
求 ∠CDF 的度数.
拓广探索
11. 如图,△ABC 的 ∠ABC 和∠ACB 的平分线 BE,CF
相交于点 G. 求证:
(1)∠BGC = 180°- ( ∠ABC + ∠ACB );
(2)∠BGC = 90°+ ∠A.
12. 如图,在四边形 ABCD 中,∠A =∠C = 90°,
BE 平分∠ABC,DF 平分 ∠CDA. 求证 BE // DF.
