【高效备课】人教版八(上) 第13章 轴对称 数学活动 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 第13章 轴对称 数学活动 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 298.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:44 | ||
图片预览








文档简介
(共24张PPT)
数学活动
R·八年级上册
新课导入
导入课题
观察这些汉字、英文字母、阿拉伯数字、花边图案及等腰三角形折叠图片,你能发现什么?
学习目标
(1)体验轴对称渗透到了我们的文化生活之中.
(2)能用轴对称设计图案.
(3)会用轴对称探讨等腰三角形性质.
推进新课
知识点1
美术字与轴对称
从轴对称的角度观察它们,你能发现它们的共同特点吗?
画出这些美术字的对称轴.
画出这些字母的对称轴.
羊 王 平 B E D
猜想下列几个未写完的美术字是什么汉字或字母?
囍 一 二 三 品
吕 中 由 甲 回
你能再写出几个轴对称的美术字吗?并画出它们的对称轴.
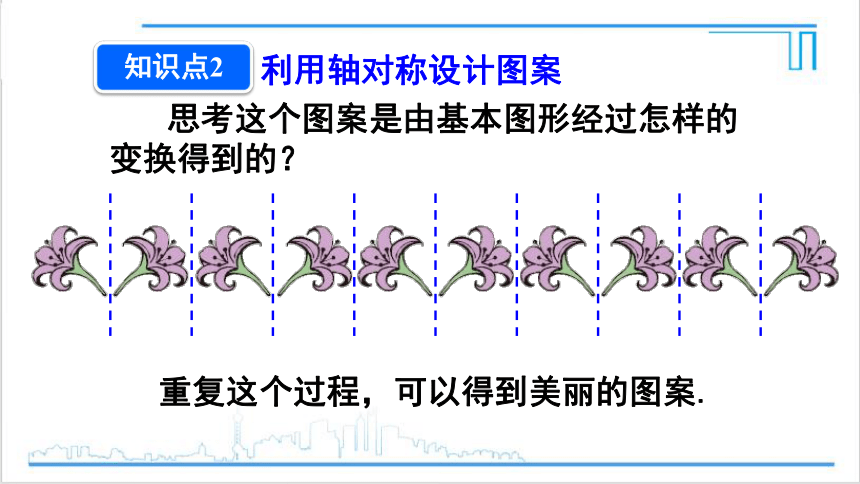
知识点2
利用轴对称设计图案
思考这个图案是由基本图形经过怎样的变换得到的?
重复这个过程,可以得到美丽的图案.
(1)改变折痕的位置并重复几次,你又得到什么?
(2)对称轴的方向和位置的变化对图形有什么影响?
请动手在一张纸上画一个你喜欢的图形,将这张纸折叠,描图,再打开纸.
对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化.
有时,将平移和轴对称结合起来,可以设计出更丰富的图案,许多镶边和背景图案就是这样设计的.
请你利用平移和轴对称设计图案.
知识点3
等腰三角形中相等的线段
等腰三角形是轴对
称图形,将△ABC沿对
称轴折叠,观察DE 与
DF 的关系.
等腰三角形底边中点到两腰的距离相等吗?
DE =DF.
如何证明呢?
A
B
E
F
C
D
D
A
F
C
B
已知:如图,在△ABC 中,AB =AC,D 是BC 边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE =DF.
∵ D 是BC 边的中点,∴ DB =DC.
∴ △EBD≌△FCD(AAS),
∴ DE =DF.
证明: ∵ DE⊥AB,DF⊥AC,
∴ ∠DEB =∠DFC =90°.
又 ∵ AB =AC,
∴ △ABC 是等腰三角形,
∴ ∠B =∠C.
如果DE,DF 分别是AB,AC 上的中线,它们还有相等的数量关系吗?
DE =DF.
A
B
C
D
E
F
证明: ∵ AB =AC,∴ ∠B =∠C.
∵ 点D,E,F 分别是BC,
AB,AC 边的中点,
∴ DB =DC,BE =AE,CF =AF.
已知:如图,在△ABC 中,AB =AC,点D,E,F分别是BC,AB,AC 边的中点.求证:DE =DF.
A
B
C
D
E
F
∴ BE =CF.
∴ △BDE ≌△CDF(SAS).
∴ DE =DF.
如果DE,DF分别是∠ADB,∠ADC 的平分线 ,它们还有相等的数量关系吗?
DE =DF.
A
B
C
D
E
F
∠CDF = ∠ADC ,
已知:如图,在△ABC 中,AB =AC,点D 是BC 边的中点,DE,DF 分别是∠ADB,∠ADC 的平分线.求证:DE =DF.
∴ ∠BDE =∠CDF ,
∴ △BDE ≌△CDF(ASA).
∴ DE =DF.
证明: ∴ ∠BDE = ∠ADB ,
A
B
C
D
E
F
随堂演练
基础巩固
1.以下列各图中的虚线为对称轴,补充图形.
2. 下列四个图形,其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
C
3. 下列图案是利用轴对称设计的吗?若是,请用虚线画出对称轴;若不是,请说明理由.
解:不是;因为它们不能关于某条直线对称.
综合应用
4.观察下列图案:
(1)图①到②是利用________得到,图③经过______或 都可以直接得到图④;
(2)由上面图案设计说明,有时需将 和_______结合起来设计图案.
轴对称
轴对称
平移
平移
轴对称
拓展延伸
5.通过折纸猜想:等腰三角形两个底角的平分线有什么关系?并利用三角形全等知识加以证明.
解:猜想,等腰三角形两个底角的平分线相等.
证明:如图.∵AB = AC,∴∠ABC =∠ACB,
∵BE平分∠ABC,CD平分∠ACB,
∴∠EBC = ∠ABC,∠DCB = ∠ACB,
∴∠EBC =∠DCB.
在△BCD和△CBE中,
∠DBC =∠ECB,
BC = CB,
∠DCB =∠EBC ,
∴△BCD≌△CBE (ASA).
∴CD = BE.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
数学活动
R·八年级上册
新课导入
导入课题
观察这些汉字、英文字母、阿拉伯数字、花边图案及等腰三角形折叠图片,你能发现什么?
学习目标
(1)体验轴对称渗透到了我们的文化生活之中.
(2)能用轴对称设计图案.
(3)会用轴对称探讨等腰三角形性质.
推进新课
知识点1
美术字与轴对称
从轴对称的角度观察它们,你能发现它们的共同特点吗?
画出这些美术字的对称轴.
画出这些字母的对称轴.
羊 王 平 B E D
猜想下列几个未写完的美术字是什么汉字或字母?
囍 一 二 三 品
吕 中 由 甲 回
你能再写出几个轴对称的美术字吗?并画出它们的对称轴.
知识点2
利用轴对称设计图案
思考这个图案是由基本图形经过怎样的变换得到的?
重复这个过程,可以得到美丽的图案.
(1)改变折痕的位置并重复几次,你又得到什么?
(2)对称轴的方向和位置的变化对图形有什么影响?
请动手在一张纸上画一个你喜欢的图形,将这张纸折叠,描图,再打开纸.
对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化.
有时,将平移和轴对称结合起来,可以设计出更丰富的图案,许多镶边和背景图案就是这样设计的.
请你利用平移和轴对称设计图案.
知识点3
等腰三角形中相等的线段
等腰三角形是轴对
称图形,将△ABC沿对
称轴折叠,观察DE 与
DF 的关系.
等腰三角形底边中点到两腰的距离相等吗?
DE =DF.
如何证明呢?
A
B
E
F
C
D
D
A
F
C
B
已知:如图,在△ABC 中,AB =AC,D 是BC 边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:DE =DF.
∵ D 是BC 边的中点,∴ DB =DC.
∴ △EBD≌△FCD(AAS),
∴ DE =DF.
证明: ∵ DE⊥AB,DF⊥AC,
∴ ∠DEB =∠DFC =90°.
又 ∵ AB =AC,
∴ △ABC 是等腰三角形,
∴ ∠B =∠C.
如果DE,DF 分别是AB,AC 上的中线,它们还有相等的数量关系吗?
DE =DF.
A
B
C
D
E
F
证明: ∵ AB =AC,∴ ∠B =∠C.
∵ 点D,E,F 分别是BC,
AB,AC 边的中点,
∴ DB =DC,BE =AE,CF =AF.
已知:如图,在△ABC 中,AB =AC,点D,E,F分别是BC,AB,AC 边的中点.求证:DE =DF.
A
B
C
D
E
F
∴ BE =CF.
∴ △BDE ≌△CDF(SAS).
∴ DE =DF.
如果DE,DF分别是∠ADB,∠ADC 的平分线 ,它们还有相等的数量关系吗?
DE =DF.
A
B
C
D
E
F
∠CDF = ∠ADC ,
已知:如图,在△ABC 中,AB =AC,点D 是BC 边的中点,DE,DF 分别是∠ADB,∠ADC 的平分线.求证:DE =DF.
∴ ∠BDE =∠CDF ,
∴ △BDE ≌△CDF(ASA).
∴ DE =DF.
证明: ∴ ∠BDE = ∠ADB ,
A
B
C
D
E
F
随堂演练
基础巩固
1.以下列各图中的虚线为对称轴,补充图形.
2. 下列四个图形,其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
C
3. 下列图案是利用轴对称设计的吗?若是,请用虚线画出对称轴;若不是,请说明理由.
解:不是;因为它们不能关于某条直线对称.
综合应用
4.观察下列图案:
(1)图①到②是利用________得到,图③经过______或 都可以直接得到图④;
(2)由上面图案设计说明,有时需将 和_______结合起来设计图案.
轴对称
轴对称
平移
平移
轴对称
拓展延伸
5.通过折纸猜想:等腰三角形两个底角的平分线有什么关系?并利用三角形全等知识加以证明.
解:猜想,等腰三角形两个底角的平分线相等.
证明:如图.∵AB = AC,∴∠ABC =∠ACB,
∵BE平分∠ABC,CD平分∠ACB,
∴∠EBC = ∠ABC,∠DCB = ∠ACB,
∴∠EBC =∠DCB.
在△BCD和△CBE中,
∠DBC =∠ECB,
BC = CB,
∠DCB =∠EBC ,
∴△BCD≌△CBE (ASA).
∴CD = BE.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
