【高效备课】人教版八(上) 第12章 全等三角形 数学活动 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 第12章 全等三角形 数学活动 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:44 | ||
图片预览





文档简介
(共23张PPT)
数学活动
——用全等形设计图案
R·八年级上册
新课导入
在我们日常生活中经常见到一些美丽的图案.
其实它们是由我们熟悉的全等形设计的,这也是我们今天的活动课题——用全等形设计图案.
学习目标:
1.了解一些由全等形设计的图案,并会从中
找出全等形.
2.认识由全等形设计的图案一般具有对称性.
3.认识由全等形设计的图案有许多相等的量
(线段、角),特殊的位置关系(垂直).
推进新课
辨别全等形
知识点1
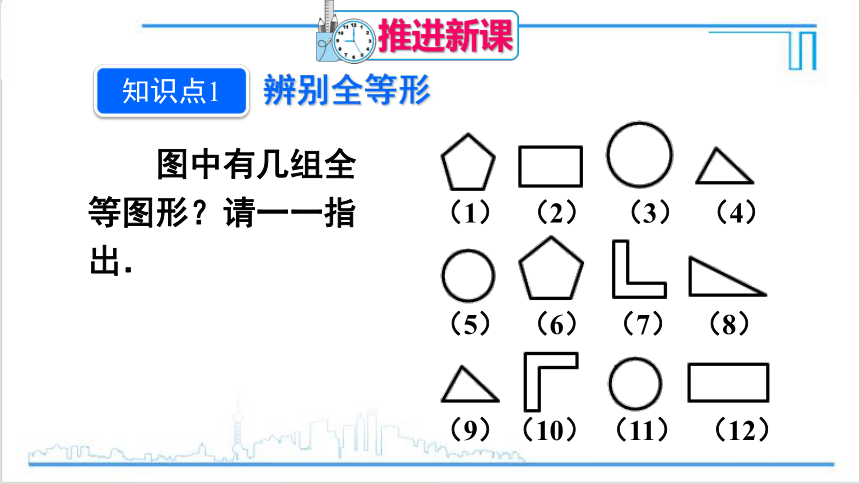
图中有几组全等图形?请一一指出.
(5) (6) (7) (8)
(9)(10) (11) (12)
(1) (2) (3) (4)
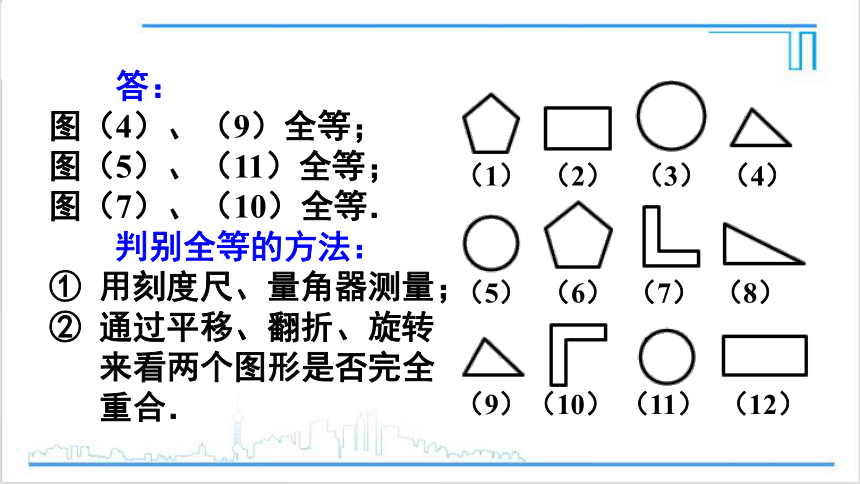
答:
图(4)、(9)全等;
图(5)、(11)全等;
图(7)、(10)全等.
判别全等的方法:
① 用刻度尺、量角器测量;
② 通过平移、翻折、旋转
来看两个图形是否完全
重合.
(5) (6) (7) (8)
(9)(10) (11) (12)
(1) (2) (3) (4)
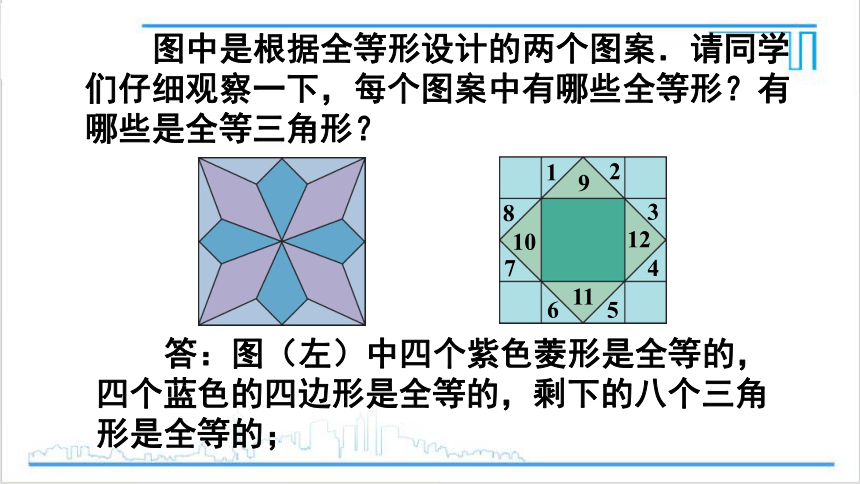
答:图(左)中四个紫色菱形是全等的,四个蓝色的四边形是全等的,剩下的八个三角形是全等的;
1
2
3
4
5
6
7
8
9
10
11
12
图中是根据全等形设计的两个图案.请同学们仔细观察一下,每个图案中有哪些全等形?有哪些是全等三角形?
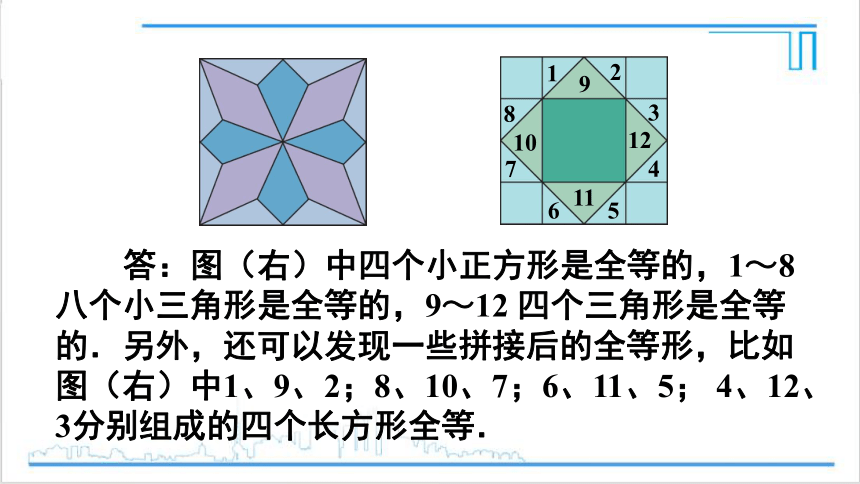
答:图(右)中四个小正方形是全等的,1~8八个小三角形是全等的,9~12 四个三角形是全等的.另外,还可以发现一些拼接后的全等形,比如图(右)中1、9、2;8、10、7;6、11、5; 4、12、3分别组成的四个长方形全等.
1
2
3
4
5
6
7
8
9
10
11
12
请同学们再举一些身边的例子与同学交流.
用全等三角形研究“筝形”
知识点2
观察这些图片,你能从图片上看出有哪些基本图形吗?
两组邻边分别相等的四边形叫做筝形.
用符号语言表示:
在四边形ABCD 中,AB = AD,BC = DC,则四边形ABCD 是筝形 .
请学生开始动手画图.
“筝形”的定义
用自己的话说说什么叫“筝形”,并在纸上
画一个“筝形” .
A
B
C
D
练习 请同学们在下列图中找出筝形,相互交流.
2
1
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A
B
C
D
O
在筝形ABCD 中,
边:AB =AD,BC =DC.
角:∠ABC =∠ADC,
∠ABD =∠ADB,∠CBD =∠CDB,
∠BAC =∠DAC,∠ACB =∠ACD.
对角线:AC⊥BD,且AC 平分BD,即BO =DO.
筝形的面积为两对角线乘积的一半.
探究“筝形”的性质
请同学们剪下“筝形ABCD”,用测量、折叠等方法可得出哪些结论?
A
B
C
D
O
追问1 你能应用所学的知识证明这些猜想吗?
证明:由“筝形”的定义可知,
AB =AD,BC =DC.
由SSS可得 △ABC ≌△ADC.
∴
由SAS可得 △ABO ≌△ADO.
∴∠ABD =∠ADB,BO=DO.
A
B
C
D
O
证明:同理 △CBO ≌△CDO,
可得 ∠CBD =∠CDB.
∴ BC=DC, OC⊥BD.
∵ △ABC ≌△ADC,
∴ “筝形”ABCD 的面积
S=2 S△ABC = 2× AC BO
= AC BD.
追问1 你能应用所学的知识证明这些猜想吗?
A
B
C
D
O
追问2 你能从边、角、对角线等方面用文字语言归纳出“筝形”所具有的性质吗?
“筝形”的性质如下:
(1)筝形两组邻边相等;
(2)筝形至少一组对角相等;
(3)筝形只有一条对角线平分一组对
角,并且垂直平分另一条对角线;
(4)筝形的面积为两对角线乘积的一半.
随堂演练
1.如图,是由全等的三角形和全等的正方形拼成的图案,观察图案,其中有______个全等的三角形,_______个全等的正方形.
基础巩固
4
5
2.请你用下面这种基本图形设计一幅图案,画在下面田字格纸上.
综合应用
3.如图,AB=AE,BC=DE,∠B=∠E,请你用测量、折纸等方法猜想AC与AD,BD与CE有什么关系?然后用全等三角形的知识证明你的结论.
拓展延伸
解:猜想:AC = AD,BD = CE.
证明:连接AC、AD、BD、CE.在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC = AD.
∴∠ACD =∠ADC,
∴∠ACB+∠ACD =∠ADE+∠ADC,
即∠BCD=∠EDC.在△BCD和△EDC中,
∴△BCD≌△EDC(SAS).
∴BD = EC.
课堂小结
A
B
C
D
O
“筝形”的性质如下:
(1)筝形两组邻边相等;
(2)筝形至少一组对角相等;
(3)筝形只有一条对角线平分一组对
角,并且垂直平分另一条对角线;
(4)筝形的面积为两对角线乘积的一半.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
数学活动
——用全等形设计图案
R·八年级上册
新课导入
在我们日常生活中经常见到一些美丽的图案.
其实它们是由我们熟悉的全等形设计的,这也是我们今天的活动课题——用全等形设计图案.
学习目标:
1.了解一些由全等形设计的图案,并会从中
找出全等形.
2.认识由全等形设计的图案一般具有对称性.
3.认识由全等形设计的图案有许多相等的量
(线段、角),特殊的位置关系(垂直).
推进新课
辨别全等形
知识点1
图中有几组全等图形?请一一指出.
(5) (6) (7) (8)
(9)(10) (11) (12)
(1) (2) (3) (4)
答:
图(4)、(9)全等;
图(5)、(11)全等;
图(7)、(10)全等.
判别全等的方法:
① 用刻度尺、量角器测量;
② 通过平移、翻折、旋转
来看两个图形是否完全
重合.
(5) (6) (7) (8)
(9)(10) (11) (12)
(1) (2) (3) (4)
答:图(左)中四个紫色菱形是全等的,四个蓝色的四边形是全等的,剩下的八个三角形是全等的;
1
2
3
4
5
6
7
8
9
10
11
12
图中是根据全等形设计的两个图案.请同学们仔细观察一下,每个图案中有哪些全等形?有哪些是全等三角形?
答:图(右)中四个小正方形是全等的,1~8八个小三角形是全等的,9~12 四个三角形是全等的.另外,还可以发现一些拼接后的全等形,比如图(右)中1、9、2;8、10、7;6、11、5; 4、12、3分别组成的四个长方形全等.
1
2
3
4
5
6
7
8
9
10
11
12
请同学们再举一些身边的例子与同学交流.
用全等三角形研究“筝形”
知识点2
观察这些图片,你能从图片上看出有哪些基本图形吗?
两组邻边分别相等的四边形叫做筝形.
用符号语言表示:
在四边形ABCD 中,AB = AD,BC = DC,则四边形ABCD 是筝形 .
请学生开始动手画图.
“筝形”的定义
用自己的话说说什么叫“筝形”,并在纸上
画一个“筝形” .
A
B
C
D
练习 请同学们在下列图中找出筝形,相互交流.
2
1
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A
B
C
D
O
在筝形ABCD 中,
边:AB =AD,BC =DC.
角:∠ABC =∠ADC,
∠ABD =∠ADB,∠CBD =∠CDB,
∠BAC =∠DAC,∠ACB =∠ACD.
对角线:AC⊥BD,且AC 平分BD,即BO =DO.
筝形的面积为两对角线乘积的一半.
探究“筝形”的性质
请同学们剪下“筝形ABCD”,用测量、折叠等方法可得出哪些结论?
A
B
C
D
O
追问1 你能应用所学的知识证明这些猜想吗?
证明:由“筝形”的定义可知,
AB =AD,BC =DC.
由SSS可得 △ABC ≌△ADC.
∴
由SAS可得 △ABO ≌△ADO.
∴∠ABD =∠ADB,BO=DO.
A
B
C
D
O
证明:同理 △CBO ≌△CDO,
可得 ∠CBD =∠CDB.
∴ BC=DC, OC⊥BD.
∵ △ABC ≌△ADC,
∴ “筝形”ABCD 的面积
S=2 S△ABC = 2× AC BO
= AC BD.
追问1 你能应用所学的知识证明这些猜想吗?
A
B
C
D
O
追问2 你能从边、角、对角线等方面用文字语言归纳出“筝形”所具有的性质吗?
“筝形”的性质如下:
(1)筝形两组邻边相等;
(2)筝形至少一组对角相等;
(3)筝形只有一条对角线平分一组对
角,并且垂直平分另一条对角线;
(4)筝形的面积为两对角线乘积的一半.
随堂演练
1.如图,是由全等的三角形和全等的正方形拼成的图案,观察图案,其中有______个全等的三角形,_______个全等的正方形.
基础巩固
4
5
2.请你用下面这种基本图形设计一幅图案,画在下面田字格纸上.
综合应用
3.如图,AB=AE,BC=DE,∠B=∠E,请你用测量、折纸等方法猜想AC与AD,BD与CE有什么关系?然后用全等三角形的知识证明你的结论.
拓展延伸
解:猜想:AC = AD,BD = CE.
证明:连接AC、AD、BD、CE.在△ABC和△AED中,
∴△ABC≌△AED(SAS).
∴AC = AD.
∴∠ACD =∠ADC,
∴∠ACB+∠ACD =∠ADE+∠ADC,
即∠BCD=∠EDC.在△BCD和△EDC中,
∴△BCD≌△EDC(SAS).
∴BD = EC.
课堂小结
A
B
C
D
O
“筝形”的性质如下:
(1)筝形两组邻边相等;
(2)筝形至少一组对角相等;
(3)筝形只有一条对角线平分一组对
角,并且垂直平分另一条对角线;
(4)筝形的面积为两对角线乘积的一半.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
