【高效备课】人教版八(上) 第13章 轴对称 章末复习 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 第13章 轴对称 章末复习 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:44 | ||
图片预览











文档简介
(共35张PPT)
章末复习
R·八年级上册
复习导入
导入课题
轴对称的知识在日常生活中应用得非常广泛,我们通过本章的学习已经了解到轴对称的相关知识,这节课我们对轴对称的知识进行系统的复习.
复习目标
(1)认识生活中的轴对称;
(2)掌握轴对称的性质;
(3)熟知等腰三角形和等边三角形的性质和判定.
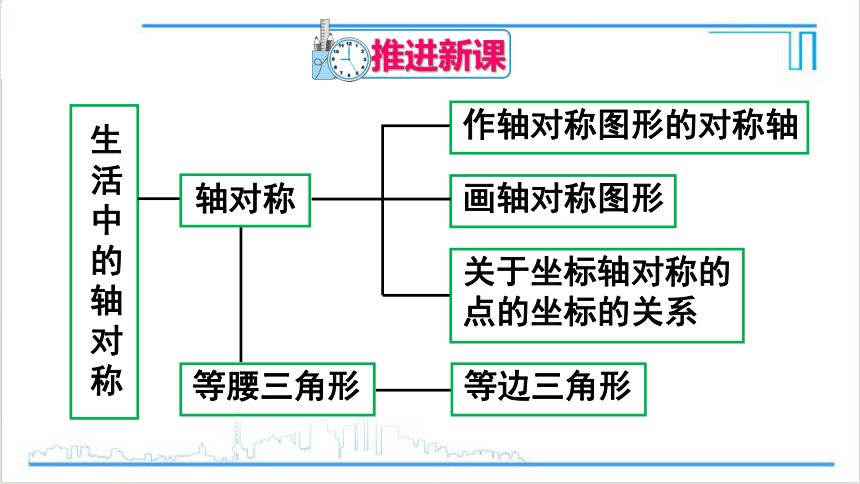
推进新课
生
活
中
的
轴
对
称
轴对称
等腰三角形
等边三角形
作轴对称图形的对称轴
画轴对称图形
关于坐标轴对称的
点的坐标的关系
1. 你能举出一些实际生活中轴对称应用的例子吗?
衣架,房梁,风筝,飞机.
知识回顾
2. 成轴对称的两个图形有哪些特点?“轴对称图形”与“成轴对称”有何区别?
成轴对称的两个图形沿对称轴折叠能够完全重合,
知识回顾
轴对称图形是指单一图形,成轴对称是指两个图形.
3. 在平面直角坐标系中,如果两个图形关于x轴或y轴对称,那么对称点的坐标有什么关系?
关于x轴对称,对称点的横坐标相等,纵坐标互为相反数;
关于y轴对称,对称点的纵坐标相等,横坐标互为相反数.
知识回顾
4. 利用等腰三角形的轴对称性,我们发现了它的哪些性质?你能通过全等三角形的知识进行证明吗?
性质一:等腰三角形的两个底角相等.
性质二:等腰三角形“三线合一”.
知识回顾
知识回顾
5. 等腰三角形和等边三角形之间有什么联系和区别?等边三角形有哪些特殊的性质?
等边三角形是特殊的等腰三角形.
等边三角形三条边相等,三个角相等且都为60°,
等边三角形每条边上都具有“三线合一”.
6. 在解决最短路径问题时,通常利用轴对称、平移等变换变“折线”为同一直线上.
知识回顾
例1 判断下列说法是否正确,如不正确,请说明原因.
(1)两个全等三角形一定关于某直线对称;
(2)等腰三角形一边上的高、中线及这边对角的平分线重合;
(3)点(3,1)与点(-3,1)关于y 轴对称;
(4)三角形中30°的角所对的边等于斜边的一半.
×
×
√
×
例2:小华在镜中看到身后墙上的钟,钟面上指针显示的时刻为8:45,那么此时的实际时间是多少?
解:此时的实际时间是3:15.
例3 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
(1)
(2)
例3 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
(3)
(4)
例4 在△ABC中,AB = AC,在AB上取一点E,在AC延长线上取一点F,使BE = CF,EF交BC于G,求证:EG = FG.
证明:如图作FD∥BE交BC的延长线于点D. 则∠B =∠D.
∵AB = AC,∴∠B =∠ACB.
又∠ACB =∠FCD,∴∠D =∠FCD,
∴FC = FD,又BE = CF,
∴BE = DF.
在△BEG和△DFG中,
∠BGE=∠DGF,
∠B =∠D,
BE = DF,
∴△BEG≌△DFG(AAS).
∴EG = FG.
例5 已知:如图,△ABC 是等边三角形,BD 是AC 边上的高,延长BC 到E,使CE = CD,过点D 作DF ⊥BE于F.求证:(1)BD = DE;
A
B
C
D
E
F
证明:∵ △ABC 是等边三角形,
∴∠ABC =∠ACB = 60°.
∵BD⊥AC,
∴∠DBC =
∠ABC = 30°.
又 CE = CD,
∴ ∠CED = ∠CDE,
∴ ∠CED =
∠ACB = 30°.
∴ ∠DBC = ∠CED,
∴ BD = DE.
A
B
C
D
E
F
求证:(2)BF = EF;
证明: 在△BDE 中,
BD = DE,DF⊥BE,
∴ BF = EF.
A
B
C
D
E
F
求证:(3)请猜想FC 与BF 间的数量关系,并说明理由.
猜想:BF = 3FC.
证明:∵ 在Rt△CDF 中,
∠ACB = 60°,
∴ ∠CDF = 30°.
∴ CD = 2FC.
A
B
C
D
E
F
又在Rt△BDC 中,
∠DBC = 30°,
∴ BC =2DC = 4FC,
即BF = 3FC.
A
B
C
D
E
F
图2
图1
例6 如图,点O到△ABC的两边AB、AC所在的直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证AB=AC;
(2)如图2,若点O在△ABC内部,求证AB=AC;
(3)若点O在△ABC外部,AB=AC成立吗?请画图表示.
(1)证明:∵OE⊥AB,OF⊥AC,
∴∠BEO=∠CFO=90°.
在Rt△BEO在Rt△CFO中,
OB = OC,
OE = OF,
∴Rt△BEO≌Rt△CFO (HL).
∴∠B=∠C. ∴AB=AC.
图1
(2)证明:作OE⊥AB,OF⊥AC,
垂足分别为E、F,
则∠BEO =∠CFO=90°.
在Rt△BEO和Rt△CFO中,
OB = OC,
OE = OF,
∴Rt△BEO≌Rt△CFO(HL).
∴∠ABO =∠ACO.
连接AO,∵OE = OF,
则AO是∠BAC的平分线,
图2
∴∠BAO =∠CAO.
在△ABO和△ACO中,
∠ABO =∠ACO,
∠BAO =∠CAO,
AO = AO,
∴△ABO≌△ACO (AAS).
∴AB =AC.
图2
(3)成立,如图所示.
随堂演练
基础巩固
一、填空
1.在轴对称图形中,对应点所连线段被________垂直平分.
2.如图,△ABC中,∠A=30°,∠C=90°,BD平分∠ABC,若AD=6cm,则AC= ___cm.
对称轴
9
二、判断
3.等腰三角形、角和圆都是轴对称图形.
×
√
4.所有的直径都是圆的对称轴.
5.在轴对称图形中,对应线段的延长线不一定交在对称轴上.
6.等腰三角形只有一条对称轴.
×
×
三、画出下列是轴对称图形的所有对称轴.
综合应用
四、如图,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于点H,HD=1,HE=2,试求BD和CE的长.
解:∵∠A = 60°,
CE⊥AB,BD⊥AC,
∴∠ACE = 30°,
∠ABD = 30°.
∵HE = 2,
∴BH = 2HE = 4.
∵HD = 1,
∴HC = 2HD = 2.
∴BD = BH + HD = 5,CE = CH + HE = 4.
拓展延伸
五、如图,点P是∠AOB内一点,∠AOB=30°,OP=10,点M、N分别是OA、OB上的动点,试通过作图说明△PMN周长的最小值是多少?
解:如图,分别作P点关于OA、OB的对称点P1,P2,连接P1P2与OA相交于点M,与OB相交于点N,则此时△PMN的周长最小(三点共线).
M
N
连接OP1,OP2,则
∠P1OP2 = 2∠AOB = 60°,
OP1 = OP = OP2,
∴△OP1P2是等边三角形,∴P1P2=OP1=OP=10,
∴PM+MN+NP
=P1M+MN+NP2
=P1P2=10.
即△PMN周长的最小值为10.
课堂小结
生
活
中
的
轴
对
称
轴对称
等腰三角形
等边三角形
作轴对称图形的对称轴
画轴对称图形
关于坐标轴对称的
点的坐标的关系
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
章末复习
R·八年级上册
复习导入
导入课题
轴对称的知识在日常生活中应用得非常广泛,我们通过本章的学习已经了解到轴对称的相关知识,这节课我们对轴对称的知识进行系统的复习.
复习目标
(1)认识生活中的轴对称;
(2)掌握轴对称的性质;
(3)熟知等腰三角形和等边三角形的性质和判定.
推进新课
生
活
中
的
轴
对
称
轴对称
等腰三角形
等边三角形
作轴对称图形的对称轴
画轴对称图形
关于坐标轴对称的
点的坐标的关系
1. 你能举出一些实际生活中轴对称应用的例子吗?
衣架,房梁,风筝,飞机.
知识回顾
2. 成轴对称的两个图形有哪些特点?“轴对称图形”与“成轴对称”有何区别?
成轴对称的两个图形沿对称轴折叠能够完全重合,
知识回顾
轴对称图形是指单一图形,成轴对称是指两个图形.
3. 在平面直角坐标系中,如果两个图形关于x轴或y轴对称,那么对称点的坐标有什么关系?
关于x轴对称,对称点的横坐标相等,纵坐标互为相反数;
关于y轴对称,对称点的纵坐标相等,横坐标互为相反数.
知识回顾
4. 利用等腰三角形的轴对称性,我们发现了它的哪些性质?你能通过全等三角形的知识进行证明吗?
性质一:等腰三角形的两个底角相等.
性质二:等腰三角形“三线合一”.
知识回顾
知识回顾
5. 等腰三角形和等边三角形之间有什么联系和区别?等边三角形有哪些特殊的性质?
等边三角形是特殊的等腰三角形.
等边三角形三条边相等,三个角相等且都为60°,
等边三角形每条边上都具有“三线合一”.
6. 在解决最短路径问题时,通常利用轴对称、平移等变换变“折线”为同一直线上.
知识回顾
例1 判断下列说法是否正确,如不正确,请说明原因.
(1)两个全等三角形一定关于某直线对称;
(2)等腰三角形一边上的高、中线及这边对角的平分线重合;
(3)点(3,1)与点(-3,1)关于y 轴对称;
(4)三角形中30°的角所对的边等于斜边的一半.
×
×
√
×
例2:小华在镜中看到身后墙上的钟,钟面上指针显示的时刻为8:45,那么此时的实际时间是多少?
解:此时的实际时间是3:15.
例3 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
(1)
(2)
例3 如图,是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形.
(3)
(4)
例4 在△ABC中,AB = AC,在AB上取一点E,在AC延长线上取一点F,使BE = CF,EF交BC于G,求证:EG = FG.
证明:如图作FD∥BE交BC的延长线于点D. 则∠B =∠D.
∵AB = AC,∴∠B =∠ACB.
又∠ACB =∠FCD,∴∠D =∠FCD,
∴FC = FD,又BE = CF,
∴BE = DF.
在△BEG和△DFG中,
∠BGE=∠DGF,
∠B =∠D,
BE = DF,
∴△BEG≌△DFG(AAS).
∴EG = FG.
例5 已知:如图,△ABC 是等边三角形,BD 是AC 边上的高,延长BC 到E,使CE = CD,过点D 作DF ⊥BE于F.求证:(1)BD = DE;
A
B
C
D
E
F
证明:∵ △ABC 是等边三角形,
∴∠ABC =∠ACB = 60°.
∵BD⊥AC,
∴∠DBC =
∠ABC = 30°.
又 CE = CD,
∴ ∠CED = ∠CDE,
∴ ∠CED =
∠ACB = 30°.
∴ ∠DBC = ∠CED,
∴ BD = DE.
A
B
C
D
E
F
求证:(2)BF = EF;
证明: 在△BDE 中,
BD = DE,DF⊥BE,
∴ BF = EF.
A
B
C
D
E
F
求证:(3)请猜想FC 与BF 间的数量关系,并说明理由.
猜想:BF = 3FC.
证明:∵ 在Rt△CDF 中,
∠ACB = 60°,
∴ ∠CDF = 30°.
∴ CD = 2FC.
A
B
C
D
E
F
又在Rt△BDC 中,
∠DBC = 30°,
∴ BC =2DC = 4FC,
即BF = 3FC.
A
B
C
D
E
F
图2
图1
例6 如图,点O到△ABC的两边AB、AC所在的直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证AB=AC;
(2)如图2,若点O在△ABC内部,求证AB=AC;
(3)若点O在△ABC外部,AB=AC成立吗?请画图表示.
(1)证明:∵OE⊥AB,OF⊥AC,
∴∠BEO=∠CFO=90°.
在Rt△BEO在Rt△CFO中,
OB = OC,
OE = OF,
∴Rt△BEO≌Rt△CFO (HL).
∴∠B=∠C. ∴AB=AC.
图1
(2)证明:作OE⊥AB,OF⊥AC,
垂足分别为E、F,
则∠BEO =∠CFO=90°.
在Rt△BEO和Rt△CFO中,
OB = OC,
OE = OF,
∴Rt△BEO≌Rt△CFO(HL).
∴∠ABO =∠ACO.
连接AO,∵OE = OF,
则AO是∠BAC的平分线,
图2
∴∠BAO =∠CAO.
在△ABO和△ACO中,
∠ABO =∠ACO,
∠BAO =∠CAO,
AO = AO,
∴△ABO≌△ACO (AAS).
∴AB =AC.
图2
(3)成立,如图所示.
随堂演练
基础巩固
一、填空
1.在轴对称图形中,对应点所连线段被________垂直平分.
2.如图,△ABC中,∠A=30°,∠C=90°,BD平分∠ABC,若AD=6cm,则AC= ___cm.
对称轴
9
二、判断
3.等腰三角形、角和圆都是轴对称图形.
×
√
4.所有的直径都是圆的对称轴.
5.在轴对称图形中,对应线段的延长线不一定交在对称轴上.
6.等腰三角形只有一条对称轴.
×
×
三、画出下列是轴对称图形的所有对称轴.
综合应用
四、如图,∠A=60°,CE⊥AB于E,BD⊥AC于D,BD与CE相交于点H,HD=1,HE=2,试求BD和CE的长.
解:∵∠A = 60°,
CE⊥AB,BD⊥AC,
∴∠ACE = 30°,
∠ABD = 30°.
∵HE = 2,
∴BH = 2HE = 4.
∵HD = 1,
∴HC = 2HD = 2.
∴BD = BH + HD = 5,CE = CH + HE = 4.
拓展延伸
五、如图,点P是∠AOB内一点,∠AOB=30°,OP=10,点M、N分别是OA、OB上的动点,试通过作图说明△PMN周长的最小值是多少?
解:如图,分别作P点关于OA、OB的对称点P1,P2,连接P1P2与OA相交于点M,与OB相交于点N,则此时△PMN的周长最小(三点共线).
M
N
连接OP1,OP2,则
∠P1OP2 = 2∠AOB = 60°,
OP1 = OP = OP2,
∴△OP1P2是等边三角形,∴P1P2=OP1=OP=10,
∴PM+MN+NP
=P1M+MN+NP2
=P1P2=10.
即△PMN周长的最小值为10.
课堂小结
生
活
中
的
轴
对
称
轴对称
等腰三角形
等边三角形
作轴对称图形的对称轴
画轴对称图形
关于坐标轴对称的
点的坐标的关系
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
