【高效备课】人教版八(上) 11.1 与三角形有关的线段 11.1.2 三角形的高、中线与角平分线 课件
文档属性
| 名称 | 【高效备课】人教版八(上) 11.1 与三角形有关的线段 11.1.2 三角形的高、中线与角平分线 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 860.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-13 17:35:44 | ||
图片预览






文档简介
(共32张PPT)
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
R·八年级上册
在与三角形有关的线段中,除了它的三边外,还有它的高、中线和角平分线,这节课我们来学习三角形的高、中线和角平分线的意义、作法和发现的规律性结论.
新课导入
学习目标:
1.了解三角形的高、中线和角平分线的意义.
2.会画出三角形的高、中线和角平分线.
3.结合图形写出三种线段分别得到的相应结论.
推进新课
理解三角形的高的概念
问题1 与三角形有关的线段,除了三条边,还有三角形的高.过三角形的一个顶点,你能画出它的对边的垂线吗?
知识点1
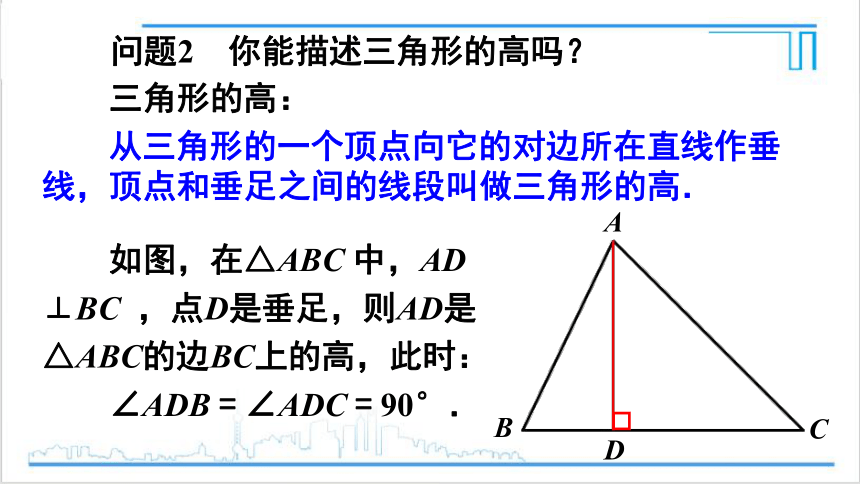
问题2 你能描述三角形的高吗?
如图,在△ABC 中,AD
⊥BC ,点D是垂足,则AD是
△ABC的边BC上的高,此时:
∠ADB = ∠ADC = 90°.
三角形的高:
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高.
A
B
C
D
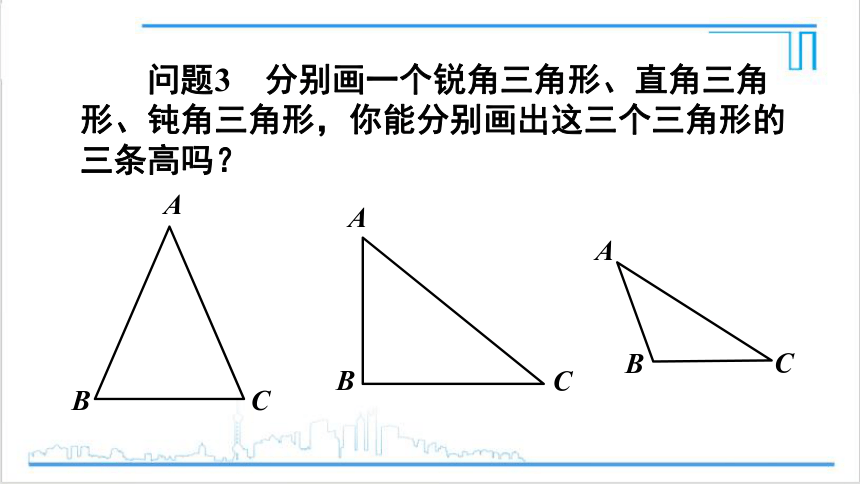
问题3 分别画一个锐角三角形、直角三角形、钝角三角形,你能分别画出这三个三角形的三条高吗?
A
C
B
A
C
B
A
C
B
锐角三角形的三条高都在三角形的内部;
直角三角形的两条高分别与两条边重合;
钝角三角形的两条高在三角形的外部.
三角形三条高所在的直线交于一点.
C
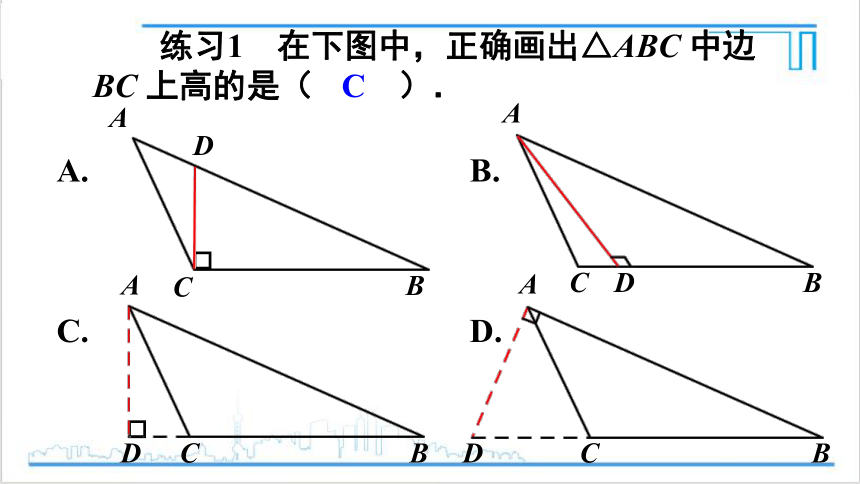
练习1 在下图中,正确画出△ABC 中边BC 上高的是( ).
A. B.
C. D.
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
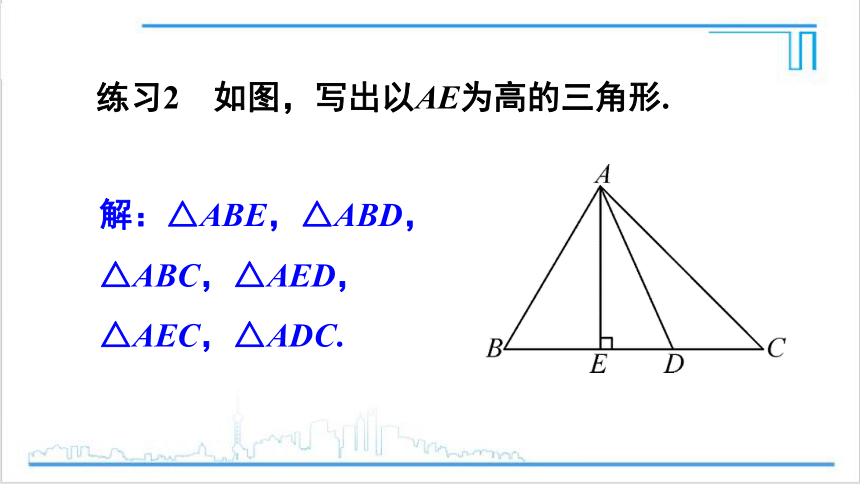
解:△ABE,△ABD,△ABC,△AED,△AEC,△ADC.
练习2 如图,写出以AE为高的三角形.
问题4 刚才我们学习了三角形的高,我们已经知道了三角形的面积公式,你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
理解三角形的中线的概念
知识点2
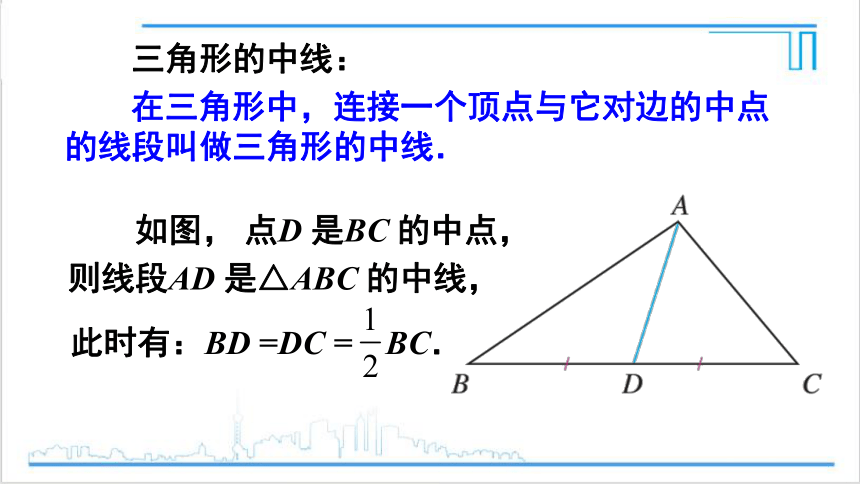
如图, 点D 是BC 的中点,
则线段AD 是△ABC 的中线,
此时有:BD =DC = BC.
三角形的中线:
在三角形中,连接一个顶点与它对边的中点的线段叫做三角形的中线.
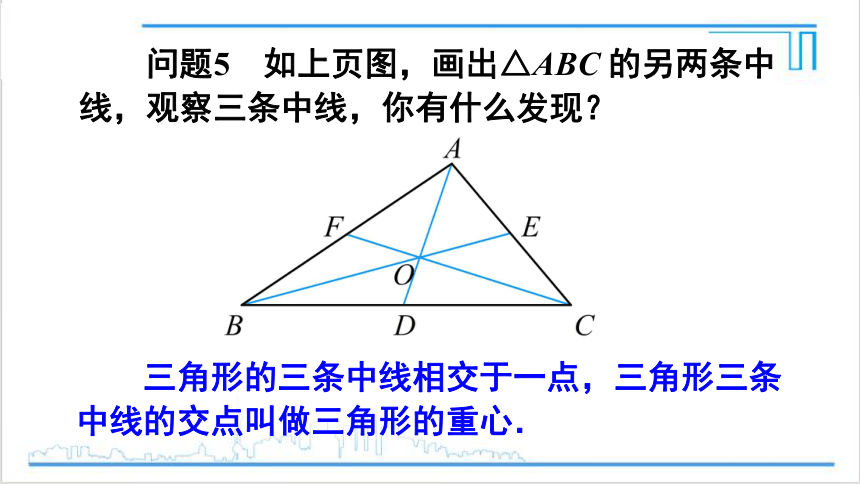
问题5 如上页图,画出△ABC 的另两条中线,观察三条中线,你有什么发现?
三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
画一个锐角三角形、直角三角形、钝角三角形,再分别画出这三个三角形的三条中线.
2
2
BD
6 cm
练习3 如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .
A
B
C
D
E
F
G
S△ABC = 2S△ABM = 40 平方厘米
练习4 如图所示,AM 是△ABC的中线,△ABM 的面积是 20 平方厘米,求△ABC 的面积.
问题6 准备一个三角形纸片ABC ,按图所示的方法折叠,展开后,折痕BD 把∠ABC 分成∠1和∠2 两个角.∠1 和∠2 有什么关系?
A
B
C
D
B
C
A
A
B
C
D
1
2
理解三角形的角平分线的概念
知识点3
三角形的角平分线:
在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
A
B
C
D
B
C
A
A
B
C
D
1
2
A
B
C
D
∠BAD =∠DAC = ∠BAC.
如图,画∠BAC 的平分线,与BC 相交于点D,则AD 是△ABC 的角平分线,此时有:
问题7 如上页图,画出△ABC 的另两条角平分线,观察三条角平分线,你有什么发现?
观察锐角三角形、直角三角形、钝角三角形的三条角平分线,你又有什么发现?
三角形的三条角平分线相交于一点.
∠2
练习5 如图,AD,BE,CF 是△ABC 的三条角平分线,则:
∠1 = ;
∠3 = ;
∠ACB =2 .
∠ABC或∠ABE
∠4或∠ACF
A
B
C
D
E
F
1
2
3
4
【课本P5 练习 第2题(2)】
练习6 如图,AD 是△ABC 的中线,AE 是∠BAC 的平分线,则BD = ________ = BC,∠BAE = _________ = ∠BAC.
DC
∠CAE
随堂演练
1.以下说法错误的是( )
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.一个三角形的三条高、中线、角平分线分别交于同一个点
A
基础巩固
2.如图,(1)(2)和(3)中的三个∠B有什么不同?这三条△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?
【课本P5 练习 第1题】
(1)
(2)
(3)
A
A
A
B
B(D)
B
C
C
C
D
∠B是锐角
∠B是直角
∠B是钝角
D
(1)
(2)
(3)
A
A
A
B
B(D)
B
C
C
C
D
∠B是锐角
∠B是直角
∠B是钝角
D
高AD在三角形内部
高AD在三角形的直角边上
高AD在三角形外部
规律:
锐角三角形的高在三角形的内部;
直角三角形的直角边上的高在另一直角边上;
钝角三角形较短边的高在三角形的外部。
3.填空:
如图,AD, BE, CF是△ABC的三条中线,
则AB=2_____________,BD=________________,
AE= _______。
【课本P5 练习 第2题(1)】
A
B
C
D
E
F
AF(或BF)
CD(或 BC)
AC
4.如图,AD是△ABC的边BC上的中线,已知AB = 5cm,AC = 3cm.△ABD的面积为a cm2,
(1)S△ABC = ______cm2;
(2)△ABD与△ACD的周长之差为___cm.
2a
2
综合应用
5.在△ABC 中,AD 是∠A 的平分线,DE∥AC 交AB于E,EF∥AD 交BC 于F,试问EF是△BED的角平分线吗?说说你的理由.
拓展延伸
解:EF是△BED的角平分线,理由如下:
∵AD是∠BAC的平分线,∴∠1=∠2.
∵ DE∥AC,
∴∠5=∠2=∠1.
∵EF∥AD,
∴∠3=∠5,∠4=∠1,
∴∠3=∠4,
∴EF 是△BED 的角平分线.
三角形中的几种重要线段
高
中线
角平
分线
课堂小结
重心
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
R·八年级上册
在与三角形有关的线段中,除了它的三边外,还有它的高、中线和角平分线,这节课我们来学习三角形的高、中线和角平分线的意义、作法和发现的规律性结论.
新课导入
学习目标:
1.了解三角形的高、中线和角平分线的意义.
2.会画出三角形的高、中线和角平分线.
3.结合图形写出三种线段分别得到的相应结论.
推进新课
理解三角形的高的概念
问题1 与三角形有关的线段,除了三条边,还有三角形的高.过三角形的一个顶点,你能画出它的对边的垂线吗?
知识点1
问题2 你能描述三角形的高吗?
如图,在△ABC 中,AD
⊥BC ,点D是垂足,则AD是
△ABC的边BC上的高,此时:
∠ADB = ∠ADC = 90°.
三角形的高:
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高.
A
B
C
D
问题3 分别画一个锐角三角形、直角三角形、钝角三角形,你能分别画出这三个三角形的三条高吗?
A
C
B
A
C
B
A
C
B
锐角三角形的三条高都在三角形的内部;
直角三角形的两条高分别与两条边重合;
钝角三角形的两条高在三角形的外部.
三角形三条高所在的直线交于一点.
C
练习1 在下图中,正确画出△ABC 中边BC 上高的是( ).
A. B.
C. D.
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
解:△ABE,△ABD,△ABC,△AED,△AEC,△ADC.
练习2 如图,写出以AE为高的三角形.
问题4 刚才我们学习了三角形的高,我们已经知道了三角形的面积公式,你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
理解三角形的中线的概念
知识点2
如图, 点D 是BC 的中点,
则线段AD 是△ABC 的中线,
此时有:BD =DC = BC.
三角形的中线:
在三角形中,连接一个顶点与它对边的中点的线段叫做三角形的中线.
问题5 如上页图,画出△ABC 的另两条中线,观察三条中线,你有什么发现?
三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
画一个锐角三角形、直角三角形、钝角三角形,再分别画出这三个三角形的三条中线.
2
2
BD
6 cm
练习3 如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .
A
B
C
D
E
F
G
S△ABC = 2S△ABM = 40 平方厘米
练习4 如图所示,AM 是△ABC的中线,△ABM 的面积是 20 平方厘米,求△ABC 的面积.
问题6 准备一个三角形纸片ABC ,按图所示的方法折叠,展开后,折痕BD 把∠ABC 分成∠1和∠2 两个角.∠1 和∠2 有什么关系?
A
B
C
D
B
C
A
A
B
C
D
1
2
理解三角形的角平分线的概念
知识点3
三角形的角平分线:
在三角形中,一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
A
B
C
D
B
C
A
A
B
C
D
1
2
A
B
C
D
∠BAD =∠DAC = ∠BAC.
如图,画∠BAC 的平分线,与BC 相交于点D,则AD 是△ABC 的角平分线,此时有:
问题7 如上页图,画出△ABC 的另两条角平分线,观察三条角平分线,你有什么发现?
观察锐角三角形、直角三角形、钝角三角形的三条角平分线,你又有什么发现?
三角形的三条角平分线相交于一点.
∠2
练习5 如图,AD,BE,CF 是△ABC 的三条角平分线,则:
∠1 = ;
∠3 = ;
∠ACB =2 .
∠ABC或∠ABE
∠4或∠ACF
A
B
C
D
E
F
1
2
3
4
【课本P5 练习 第2题(2)】
练习6 如图,AD 是△ABC 的中线,AE 是∠BAC 的平分线,则BD = ________ = BC,∠BAE = _________ = ∠BAC.
DC
∠CAE
随堂演练
1.以下说法错误的是( )
A.三角形的三条高一定在三角形内部交于一点
B.三角形的三条中线一定在三角形内部交于一点
C.三角形的三条角平分线一定在三角形内部交于一点
D.一个三角形的三条高、中线、角平分线分别交于同一个点
A
基础巩固
2.如图,(1)(2)和(3)中的三个∠B有什么不同?这三条△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?
【课本P5 练习 第1题】
(1)
(2)
(3)
A
A
A
B
B(D)
B
C
C
C
D
∠B是锐角
∠B是直角
∠B是钝角
D
(1)
(2)
(3)
A
A
A
B
B(D)
B
C
C
C
D
∠B是锐角
∠B是直角
∠B是钝角
D
高AD在三角形内部
高AD在三角形的直角边上
高AD在三角形外部
规律:
锐角三角形的高在三角形的内部;
直角三角形的直角边上的高在另一直角边上;
钝角三角形较短边的高在三角形的外部。
3.填空:
如图,AD, BE, CF是△ABC的三条中线,
则AB=2_____________,BD=________________,
AE= _______。
【课本P5 练习 第2题(1)】
A
B
C
D
E
F
AF(或BF)
CD(或 BC)
AC
4.如图,AD是△ABC的边BC上的中线,已知AB = 5cm,AC = 3cm.△ABD的面积为a cm2,
(1)S△ABC = ______cm2;
(2)△ABD与△ACD的周长之差为___cm.
2a
2
综合应用
5.在△ABC 中,AD 是∠A 的平分线,DE∥AC 交AB于E,EF∥AD 交BC 于F,试问EF是△BED的角平分线吗?说说你的理由.
拓展延伸
解:EF是△BED的角平分线,理由如下:
∵AD是∠BAC的平分线,∴∠1=∠2.
∵ DE∥AC,
∴∠5=∠2=∠1.
∵EF∥AD,
∴∠3=∠5,∠4=∠1,
∴∠3=∠4,
∴EF 是△BED 的角平分线.
三角形中的几种重要线段
高
中线
角平
分线
课堂小结
重心
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
