北师版》北师版数学必修2》第二章解析几何初步》直线与直线的方程
文档属性
| 名称 | 北师版》北师版数学必修2》第二章解析几何初步》直线与直线的方程 |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-13 21:19:00 | ||
图片预览








文档简介
(共28张PPT)
有人说,现代数学起源于解析几何与微积分的发明。这样说是很有道理的,我们知道,在欧氏几何中,所用的研究方法是以公理为基础,直接依据图形中点、直线、平面的关系研究图形的性质。
在平面解析几何中,所用的研究方法与欧氏几何不同,
它是在直角坐标系的基础上,用坐标表示点,用方程表示曲线(包括直线),通过方程研究曲线的性质,通过方程组的解研究几何图形之间的位置关系,因此,可以说,解析几何是用代数方法研究几何问题的一门学科。
由于代数方法的主要特点是“算”,当几何问题代数化之后,可以用计算机处理代数问题,从而实现机器证明。我国数学家吴文俊在这方面有突出的贡献,它提出的方法被称为“吴方法”。
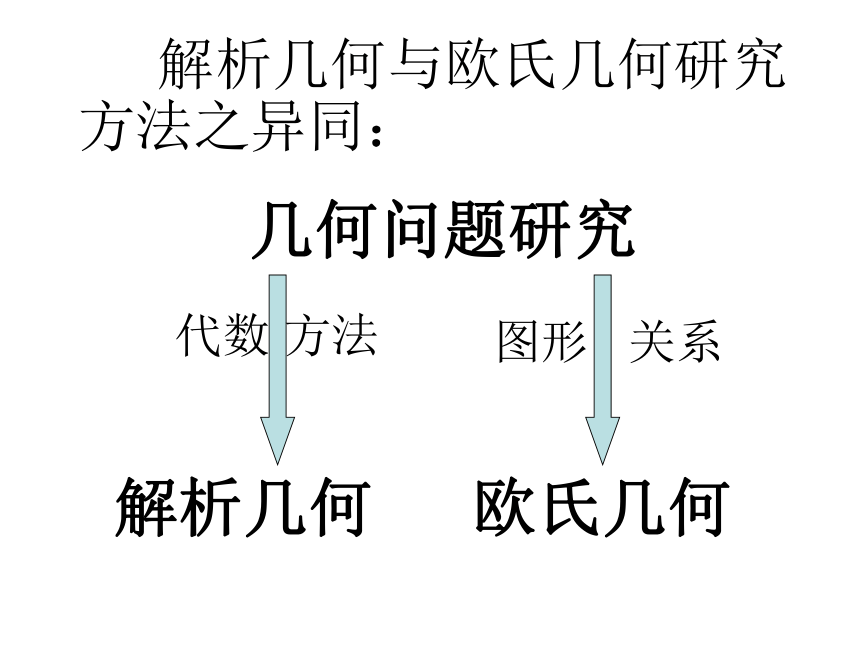
解析几何与欧氏几何研究方法之异同:
几何问题研究
解析几何
代数 方法
欧氏几何
图形 关系
17世纪,法国数学家笛卡尔创立了解析几何,笛卡尔为什么会创立解析几何?这有着深刻的背景,他于1637年发表了著名的哲学著作《更好地指导推理和寻求科学真理的方法论》,该书有三个附录,解析几何的发明就包含在其中之一的《几何学》中。
这就是意味着解析几何及他的其它发明是在其方法论原理的指导下获得的,笛卡尔方法论原理的本旨是寻求发现真理的一般方法,他曾称自己设想的一般方法为“通用数学”,
笛卡尔设想的“通用数学”方法
任何问题
数学问题
代数问题
方程求解
平面解析几何研究的主要问题是:
(1) 根据已知条件,求出表示平面曲线(包括直线)的方程;
(2)通过方程研究平面曲线(包括直线)的性质。
解析几何研究问题的一般方法
几何对象的性质、位置关系
几何问题
代数问题
代数问题的解
坐标法
还原
运算 推理
如果你手中只有一把斜边长度小于下图中对角线长度的等腰直角三角形直尺,你能画出下图中的对角线吗?
一个点和直线的方向。
确定直线位置的几何要素有两个:
在直角坐标系中,过一点可以作无数条直线,这些直线组成“直线束”,它们的共同点是经过同一点,不同点是倾斜程度不同。
X
Y
O
X
Y
O
要确定直线,我们还需要什么条件呢?
直线的倾斜角的定义:
直线与x轴平行或重合时,规定其倾斜角为00。
对于一条与x轴相交的直线 ,把x轴(正方向)按逆时针方向绕着交点旋转到和直线 重合所成的角,叫着直线 的倾斜角。
x
y
直线的倾斜角的范围直线的倾斜角.gsp是什么呢?
直线的倾斜角的取值范围是:
[00, 1800)
直线倾斜角的定义有下面二个要点:
(1)直线和x轴有交点;
(2)直线绕着交点按逆时针方向旋转;
.
Y
.
Y
X
p
O
X
p
O
X
.
p
Y
O
X
.
p
Y
O
(1)
(2)
(4)
(3)
o
o
我们在日常生活中,还会遇到一个叫“坡度”的概念,坡度即是坡面的铅直高度和水平长度之比。常用千分之几(铁路)或百分之几(公路)表示。
0.4km
1km
0.8km
1km
0.8km
1km
O
x
y
0.4km
“坡度”的定义对我们 定义直线的斜率有什么启示呢?
类似地,如果我们也想给直线用一个新的量(不用倾斜角)来表示倾斜程度,不妨把这一个量叫斜率,那么你认为应该怎样定义斜率呢?
X
p
Y
O
.
(1,k)
Q(1,0)
直线的斜率定义及表达式:
过原点的直线上的点O(0,0),P(1,k),横坐标从0到1增加一个
单位时,纵坐标也从0变为到k,则
称k为直线的斜率。
X
.
p
Y
O
(1)
K>0
X
.
p
Y
O
(2)
K<0
X
.
p
Y
O
(3)
o
K不存在
X
.
p
Y
O
(4)
o
K=0
直线的斜率定义及表达式:
倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。常用k表示,即 k = tanα,k的值的变化趋势是什么呢?
X
p
Y
O
(1,k)
Q(1,0)
直线的斜率的定义:
例题 求过已知两点的直线的斜率:
(1)直线PQ过点P(2,3),Q(4,5);
(2)直线AB过点A(-2,4),B(4,-2).
练习 书本77页练习1,3,4,5.
布置作业
阅读课本第114页阅读材料,自己上网查阅相关资料,
写一篇与解析几何历史的小论文。
有人说,现代数学起源于解析几何与微积分的发明。这样说是很有道理的,我们知道,在欧氏几何中,所用的研究方法是以公理为基础,直接依据图形中点、直线、平面的关系研究图形的性质。
在平面解析几何中,所用的研究方法与欧氏几何不同,
它是在直角坐标系的基础上,用坐标表示点,用方程表示曲线(包括直线),通过方程研究曲线的性质,通过方程组的解研究几何图形之间的位置关系,因此,可以说,解析几何是用代数方法研究几何问题的一门学科。
由于代数方法的主要特点是“算”,当几何问题代数化之后,可以用计算机处理代数问题,从而实现机器证明。我国数学家吴文俊在这方面有突出的贡献,它提出的方法被称为“吴方法”。
解析几何与欧氏几何研究方法之异同:
几何问题研究
解析几何
代数 方法
欧氏几何
图形 关系
17世纪,法国数学家笛卡尔创立了解析几何,笛卡尔为什么会创立解析几何?这有着深刻的背景,他于1637年发表了著名的哲学著作《更好地指导推理和寻求科学真理的方法论》,该书有三个附录,解析几何的发明就包含在其中之一的《几何学》中。
这就是意味着解析几何及他的其它发明是在其方法论原理的指导下获得的,笛卡尔方法论原理的本旨是寻求发现真理的一般方法,他曾称自己设想的一般方法为“通用数学”,
笛卡尔设想的“通用数学”方法
任何问题
数学问题
代数问题
方程求解
平面解析几何研究的主要问题是:
(1) 根据已知条件,求出表示平面曲线(包括直线)的方程;
(2)通过方程研究平面曲线(包括直线)的性质。
解析几何研究问题的一般方法
几何对象的性质、位置关系
几何问题
代数问题
代数问题的解
坐标法
还原
运算 推理
如果你手中只有一把斜边长度小于下图中对角线长度的等腰直角三角形直尺,你能画出下图中的对角线吗?
一个点和直线的方向。
确定直线位置的几何要素有两个:
在直角坐标系中,过一点可以作无数条直线,这些直线组成“直线束”,它们的共同点是经过同一点,不同点是倾斜程度不同。
X
Y
O
X
Y
O
要确定直线,我们还需要什么条件呢?
直线的倾斜角的定义:
直线与x轴平行或重合时,规定其倾斜角为00。
对于一条与x轴相交的直线 ,把x轴(正方向)按逆时针方向绕着交点旋转到和直线 重合所成的角,叫着直线 的倾斜角。
x
y
直线的倾斜角的范围直线的倾斜角.gsp是什么呢?
直线的倾斜角的取值范围是:
[00, 1800)
直线倾斜角的定义有下面二个要点:
(1)直线和x轴有交点;
(2)直线绕着交点按逆时针方向旋转;
.
Y
.
Y
X
p
O
X
p
O
X
.
p
Y
O
X
.
p
Y
O
(1)
(2)
(4)
(3)
o
o
我们在日常生活中,还会遇到一个叫“坡度”的概念,坡度即是坡面的铅直高度和水平长度之比。常用千分之几(铁路)或百分之几(公路)表示。
0.4km
1km
0.8km
1km
0.8km
1km
O
x
y
0.4km
“坡度”的定义对我们 定义直线的斜率有什么启示呢?
类似地,如果我们也想给直线用一个新的量(不用倾斜角)来表示倾斜程度,不妨把这一个量叫斜率,那么你认为应该怎样定义斜率呢?
X
p
Y
O
.
(1,k)
Q(1,0)
直线的斜率定义及表达式:
过原点的直线上的点O(0,0),P(1,k),横坐标从0到1增加一个
单位时,纵坐标也从0变为到k,则
称k为直线的斜率。
X
.
p
Y
O
(1)
K>0
X
.
p
Y
O
(2)
K<0
X
.
p
Y
O
(3)
o
K不存在
X
.
p
Y
O
(4)
o
K=0
直线的斜率定义及表达式:
倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。常用k表示,即 k = tanα,k的值的变化趋势是什么呢?
X
p
Y
O
(1,k)
Q(1,0)
直线的斜率的定义:
例题 求过已知两点的直线的斜率:
(1)直线PQ过点P(2,3),Q(4,5);
(2)直线AB过点A(-2,4),B(4,-2).
练习 书本77页练习1,3,4,5.
布置作业
阅读课本第114页阅读材料,自己上网查阅相关资料,
写一篇与解析几何历史的小论文。
