从分数到分式
图片预览





文档简介
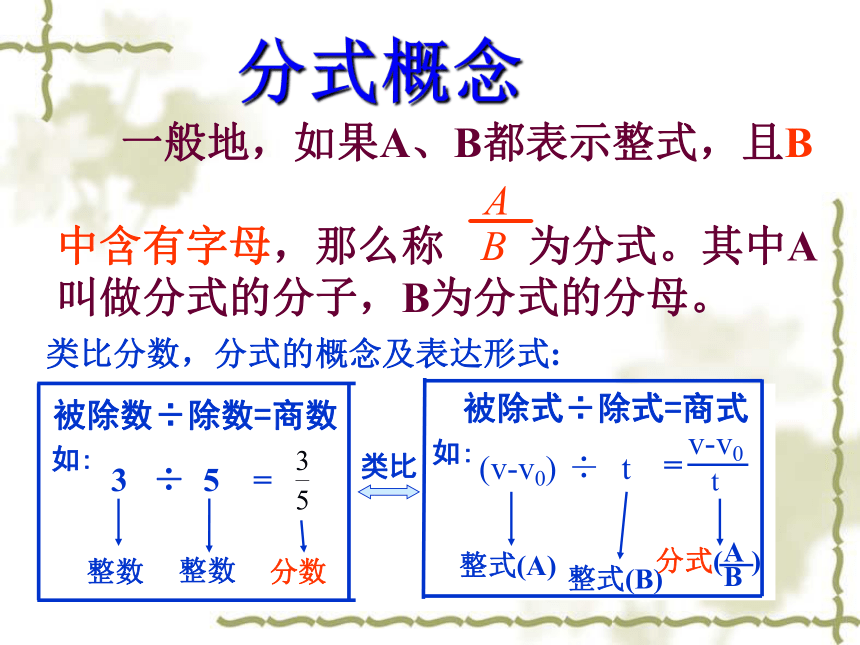
课件15张PPT。16.1.1 从分数到分式1、长方形的面积为20cm2,宽为9cm,则长为___;又若一块长方形的田地面积为m,其中宽是n ,则 长应为:———— ? 思考2、把体积为100cm3的水倒入底面积为13cm2的圆柱形的容器中,水面高度为————cm;若把体积为60的水倒入面积为S的圆柱形容器中,水面高度为————3、一艘轮船在静水中的最大航速为20千米/时,若江水的流速为x千米/时,则它沿江以最大航速顺流航行100千米所用时间为——,以最大航速逆流航行60千米的时间为——。它们有什么共同特征?分母中有、无字母观察:从上例子可得到这一些代数式:又有什么不同点?(观察分母)都具有分数的形式分式概念 一般地,如果A、B都表示整式,且B
中含有字母,那么称 为分式。其中A叫做分式的分子,B为分式的分母。类比分数,分式的概念及表达形式:
整数整数分数
t整式(A)整式(B)类比(v-v0)÷t=v-v03 ÷ 5 = 被除数÷除数=商数如:被除式÷除式=商式如:思考:
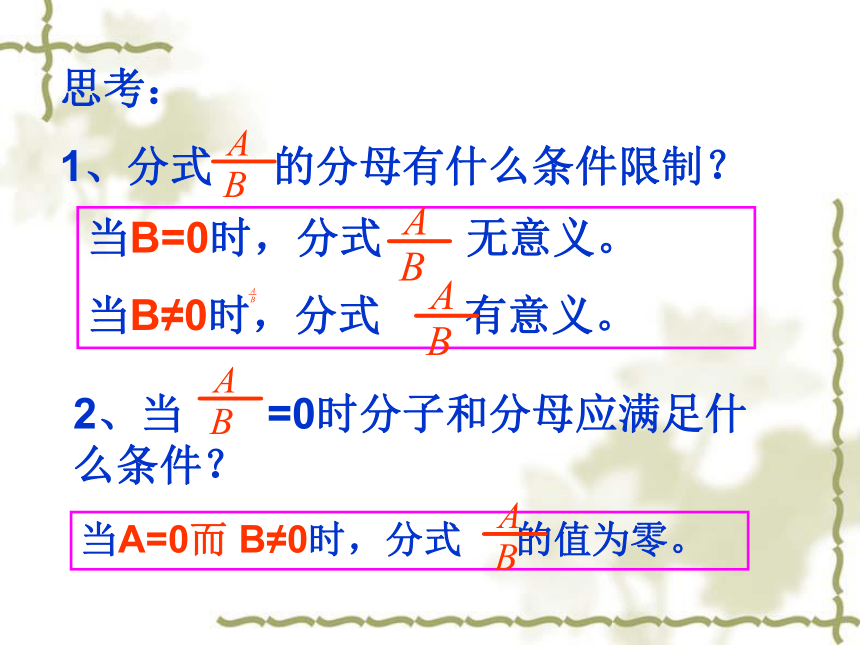
1、分式 的分母有什么条件限制?当B=0时,分式 无意义。
当B≠0时,分式 有意义。2、当 =0时分子和分母应满足什么条件?当A=0而 B≠0时,分式 的值为零。概念辨析5x-7, 3x2-1, -5,答:是分式下列各式中,哪些是分式?哪些是整式?(2) 当x为何值时,分式有意义? (1) 当x为何值时,分式无意义?例1. 已知分式 , (2)由(1)得 当x ≠-2时,分式有意义 ∴当x = -2时分式:解:(1)当分母等于零时,分式无意义。∴ x = -2即 x+2=0例2. 已知分式 ,(4) 当x= - 3时,分式的值是多少?(3) 当x为何值时,分式的值为零?(4)当x = -3时,解:(3)当分子等于零而分母不等于零时,分式的值为零。∴ x ≠ -2而 x+2≠0∴x = ±2则 x2 - 4=0例3、甲、乙两人从一条公路的某处出发,同向而行,已知甲每时行a千米,乙每时行b千米,且a>b、如果乙提前1小时出发,那么:(3)若取a=5, b=5时,你所得到的分式有意义吗? (2)当a=6,b=5时,求甲追上乙所需的时间?(1)甲追上乙需要多少时间?它所表示的实际意义是什么?解: 由题意得,乙先行1小时的路程是b千米,甲比乙每时多行(a-b) 千米,即每时能追(a-b) 千米。(1)甲追上乙所需的时间是:(2)当a=6,b=5时,甲追上乙所需的时间是:它表示甲永远追不上乙。A: ①③④;B: ②③④;C: ②③⑤;D: ①②⑤.巩固练习1:中是分式的是( )1:代数式2:当x=-1时,下列分式没有意义的是( )A. B. C. D.1x取全体实数巩固练习2:2:归纳:1:你这节课有什么收获?课堂小结A = 0 且 B≠0 B≠0 作业:1:教科书10页:习题1、2、3、8、9、13 2:思考:找出一些与分式有关的实际例子。再见祝同学们共同进步!
中含有字母,那么称 为分式。其中A叫做分式的分子,B为分式的分母。类比分数,分式的概念及表达形式:
整数整数分数
t整式(A)整式(B)类比(v-v0)÷t=v-v03 ÷ 5 = 被除数÷除数=商数如:被除式÷除式=商式如:思考:
1、分式 的分母有什么条件限制?当B=0时,分式 无意义。
当B≠0时,分式 有意义。2、当 =0时分子和分母应满足什么条件?当A=0而 B≠0时,分式 的值为零。概念辨析5x-7, 3x2-1, -5,答:是分式下列各式中,哪些是分式?哪些是整式?(2) 当x为何值时,分式有意义? (1) 当x为何值时,分式无意义?例1. 已知分式 , (2)由(1)得 当x ≠-2时,分式有意义 ∴当x = -2时分式:解:(1)当分母等于零时,分式无意义。∴ x = -2即 x+2=0例2. 已知分式 ,(4) 当x= - 3时,分式的值是多少?(3) 当x为何值时,分式的值为零?(4)当x = -3时,解:(3)当分子等于零而分母不等于零时,分式的值为零。∴ x ≠ -2而 x+2≠0∴x = ±2则 x2 - 4=0例3、甲、乙两人从一条公路的某处出发,同向而行,已知甲每时行a千米,乙每时行b千米,且a>b、如果乙提前1小时出发,那么:(3)若取a=5, b=5时,你所得到的分式有意义吗? (2)当a=6,b=5时,求甲追上乙所需的时间?(1)甲追上乙需要多少时间?它所表示的实际意义是什么?解: 由题意得,乙先行1小时的路程是b千米,甲比乙每时多行(a-b) 千米,即每时能追(a-b) 千米。(1)甲追上乙所需的时间是:(2)当a=6,b=5时,甲追上乙所需的时间是:它表示甲永远追不上乙。A: ①③④;B: ②③④;C: ②③⑤;D: ①②⑤.巩固练习1:中是分式的是( )1:代数式2:当x=-1时,下列分式没有意义的是( )A. B. C. D.1x取全体实数巩固练习2:2:归纳:1:你这节课有什么收获?课堂小结A = 0 且 B≠0 B≠0 作业:1:教科书10页:习题1、2、3、8、9、13 2:思考:找出一些与分式有关的实际例子。再见祝同学们共同进步!
