数学人教A版(2019)选择性必修第一册2.2.2直线的两点式方程(共37张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.2直线的两点式方程(共37张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 05:50:23 | ||
图片预览











文档简介
(共37张PPT)
直线的两点式方程
(一)温故设疑、引入新课
(1) 一个点与直线的方向可以确定一条直线;
(2) 两个点确定一条直线.
(一)温故设疑、引入新课
(一)温故设疑、引入新课
(一)温故设疑、引入新课
一样. 两个点确定唯一一条直线.
(一)温故设疑、引入新课
(一)温故设疑、引入新课
给定两个点,这两个点可以确定直线方向,因此这其实与一个点和直线的方向确定一条直线是一致的,转化的关键是处理直线上任意一点的坐标(x,y)与两个已知点P1, P2的坐标之间的关系.
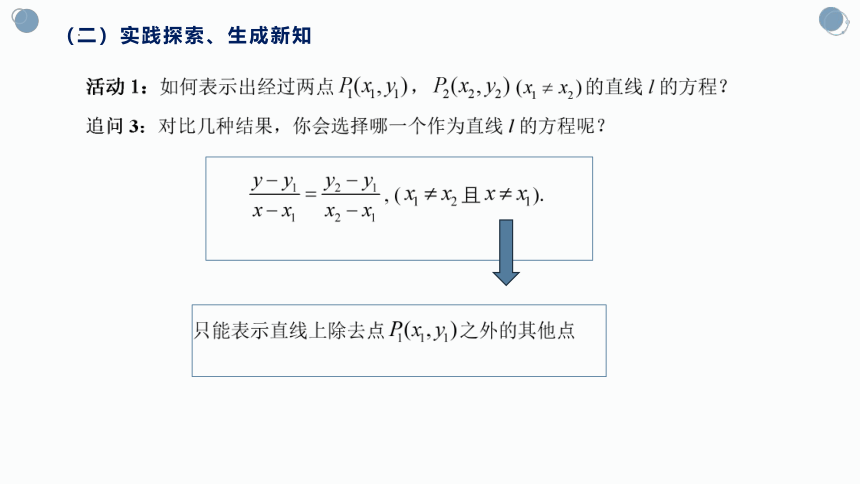
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
不对称,不美观
对称,美观
对称,美观
整理可得一般式
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
直线的两点式方程:
(二)实践探索、生成新知
直线的点斜式方程
(二)实践探索、生成新知
直线的两点式方程
斜率
建立坐标之间的关系
基础
(二)实践探索、生成新知
只能表示除了平行或垂直于x轴之外的其他直线.
不能
(二)实践探索、生成新知
直线的截距式方程:
(二)实践探索、生成新知
(二)实践探索、生成新知
不能表示平行或垂直于x轴的直线以及过原点的直线.
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
区别:四种方程是通过已知不同类型的几何要素推导出来的,方程的应用条件不同,呈现的表达形式也不同;
联系:四种方程都是对直线的定量刻画,都突出了点斜式的核心地位,都涉及到确定直线的两个基本要素:一点一方向,均可以直接将直线上任意点的几何特征利用几何要素的代数形式进行刻画,得到直线的代数表示,即直线上点的横纵坐标x,y之间关系,且这四种方程均有各自的限制条件.
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
提示与注意:
当已知两点坐标,求过这两点的直线方程时,首先要判断是否满足两点式方程的适用条件:两点的连线不垂直于坐标轴,当给定参数时,一定先考虑是否满足两点式方程的适用条件.若满足,才考虑用两点式求方程,若不确定,则需要分类讨论.
由于减法的顺序性,一般用两点式求直线方程时常会将字母或数字的顺序错位而导致错误.在记忆和使用两点式方程时,必须注意坐标的对应关系.
(三)应用探索、加深理解
(三)应用探索、加深理解
截距式方程适用条件
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
提示与注意:
如果问题中涉及直线与坐标轴相交,则可考虑选用截距式求直线方程,用待定系数法确定其系数即可;
选用截距式求直线方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.如果题中出现直线在两坐标轴上的“截距相等”“截距互为相反数”等条件时,采用截距式求直线方程,要注意考虑“零截距”的情况.因此在解决问题时注意两点式与截距式适用条件限制需要分类讨论.
(三)应用探索、加深理解
(四)反思总结、形成体系
通过本节课学习,你都掌握了哪些新的知识与方法?有哪些收获?
(四)反思总结、形成体系
通过本节课学习,你都掌握了哪些新的知识与方法?有哪些收获?
特殊化
特殊化
用两点坐标表示斜率
类比、特殊到一般、一般到特殊
数学抽象、数学运算、逻辑推理
直线的两点式方程
(一)温故设疑、引入新课
(1) 一个点与直线的方向可以确定一条直线;
(2) 两个点确定一条直线.
(一)温故设疑、引入新课
(一)温故设疑、引入新课
(一)温故设疑、引入新课
一样. 两个点确定唯一一条直线.
(一)温故设疑、引入新课
(一)温故设疑、引入新课
给定两个点,这两个点可以确定直线方向,因此这其实与一个点和直线的方向确定一条直线是一致的,转化的关键是处理直线上任意一点的坐标(x,y)与两个已知点P1, P2的坐标之间的关系.
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
不对称,不美观
对称,美观
对称,美观
整理可得一般式
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
直线的两点式方程:
(二)实践探索、生成新知
直线的点斜式方程
(二)实践探索、生成新知
直线的两点式方程
斜率
建立坐标之间的关系
基础
(二)实践探索、生成新知
只能表示除了平行或垂直于x轴之外的其他直线.
不能
(二)实践探索、生成新知
直线的截距式方程:
(二)实践探索、生成新知
(二)实践探索、生成新知
不能表示平行或垂直于x轴的直线以及过原点的直线.
(二)实践探索、生成新知
(二)实践探索、生成新知
(二)实践探索、生成新知
区别:四种方程是通过已知不同类型的几何要素推导出来的,方程的应用条件不同,呈现的表达形式也不同;
联系:四种方程都是对直线的定量刻画,都突出了点斜式的核心地位,都涉及到确定直线的两个基本要素:一点一方向,均可以直接将直线上任意点的几何特征利用几何要素的代数形式进行刻画,得到直线的代数表示,即直线上点的横纵坐标x,y之间关系,且这四种方程均有各自的限制条件.
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
提示与注意:
当已知两点坐标,求过这两点的直线方程时,首先要判断是否满足两点式方程的适用条件:两点的连线不垂直于坐标轴,当给定参数时,一定先考虑是否满足两点式方程的适用条件.若满足,才考虑用两点式求方程,若不确定,则需要分类讨论.
由于减法的顺序性,一般用两点式求直线方程时常会将字母或数字的顺序错位而导致错误.在记忆和使用两点式方程时,必须注意坐标的对应关系.
(三)应用探索、加深理解
(三)应用探索、加深理解
截距式方程适用条件
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
(三)应用探索、加深理解
提示与注意:
如果问题中涉及直线与坐标轴相交,则可考虑选用截距式求直线方程,用待定系数法确定其系数即可;
选用截距式求直线方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.如果题中出现直线在两坐标轴上的“截距相等”“截距互为相反数”等条件时,采用截距式求直线方程,要注意考虑“零截距”的情况.因此在解决问题时注意两点式与截距式适用条件限制需要分类讨论.
(三)应用探索、加深理解
(四)反思总结、形成体系
通过本节课学习,你都掌握了哪些新的知识与方法?有哪些收获?
(四)反思总结、形成体系
通过本节课学习,你都掌握了哪些新的知识与方法?有哪些收获?
特殊化
特殊化
用两点坐标表示斜率
类比、特殊到一般、一般到特殊
数学抽象、数学运算、逻辑推理
