1.3 勾股定理的应用 同步练习(无答案) 2023-2024学年北师大版数学八年级上册
文档属性
| 名称 | 1.3 勾股定理的应用 同步练习(无答案) 2023-2024学年北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 124.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-15 14:02:55 | ||
图片预览

文档简介
1.3 勾股定理的应用
一、单选题
1.已知一直角三角形的木板,三边的平方和为1800cm2,则斜边长为( )
A.30cm B.80cm C.90cm D.120cm
2.一根旗杆在离地面3米处断裂,旗杆顶部落在离旗杆底部4米处,旗杆折断之前的高度是( )
A.5米 B.7米 C.8米 D.9米
3.如图,斜面AC的坡比CD:AD=1:2.AC=3 m,坡有一旗杆BC.旗杆顶端B点与A点有一条绝缘钢端相连,若AB=10m.则旗杆BC的高度( )
A.5m B.6m C.8m D.(3+ )m
4.如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏 问登陆点A与宝藏埋藏点B之间的距离是 .
A.10 B.11 C.12 D.13
5.如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离的走法共有( )
A.1种 B.2种 C.3种 D.4种
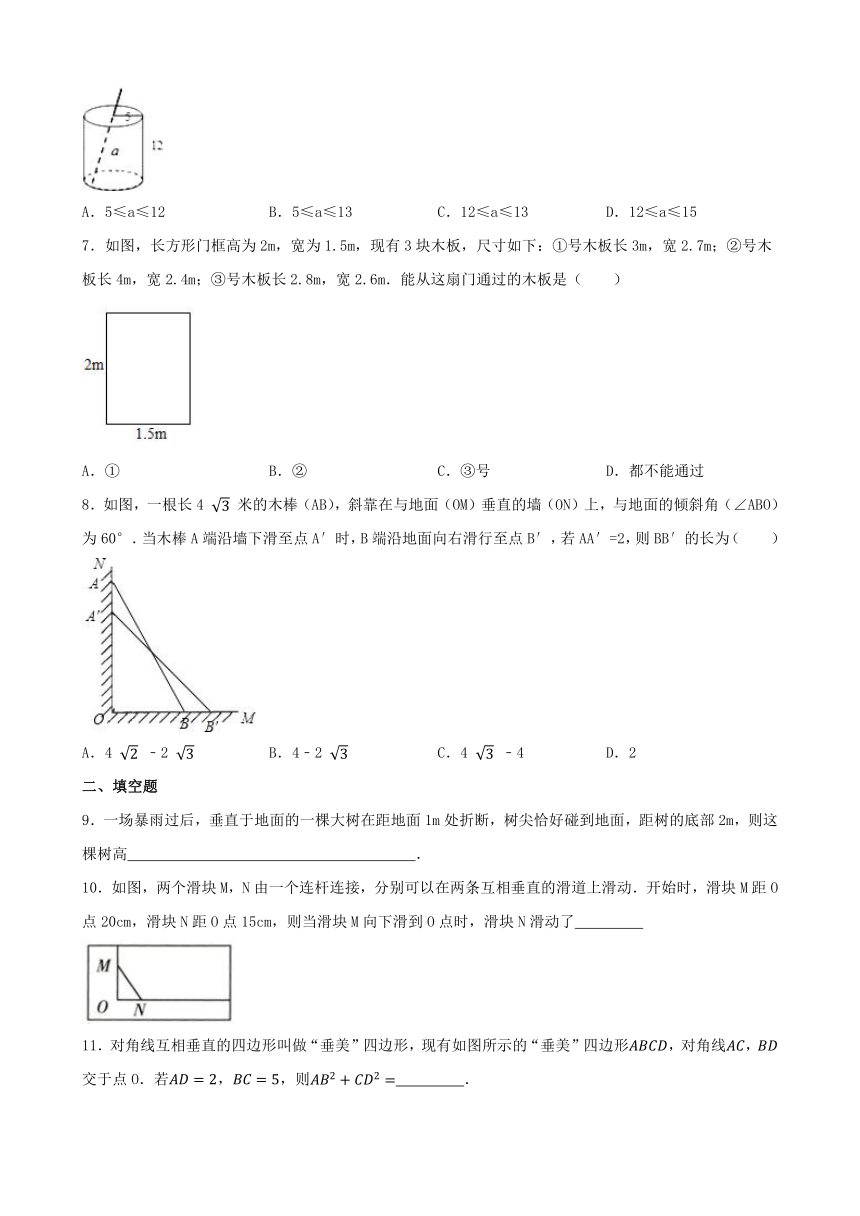
6.如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
7.如图,长方形门框高为2m,宽为1.5m,现有3块木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.6m.能从这扇门通过的木板是( )
A.① B.② C.③号 D.都不能通过
8.如图,一根长4 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′,若AA′=2,则BB′的长为( )
A.4 ﹣2 B.4﹣2 C.4 ﹣4 D.2
二、填空题
9.一场暴雨过后,垂直于地面的一棵大树在距地面1m处折断,树尖恰好碰到地面,距树的底部2m,则这棵树高 .
10.如图,两个滑块M,N由一个连杆连接,分别可以在两条互相垂直的滑道上滑动.开始时,滑块M距O点20cm,滑块N距O点15cm,则当滑块M向下滑到O点时,滑块N滑动了
11.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线,交于点O.若,,则 .
12.有一辆装满货物的卡车,宽2.4米(货物的顶部是水平的),要通过如图所示的截面的上半部分是半圆,下半部分长方形的单向道,已知半圆的直径为4米,长方形竖直的一条边长是2.5米,则卡车的外形高必须低于 米.
13.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合2寸,问门广几何?”意思是:如图推开两扇门( 和 ),门边沿D,C两点到门槛 的距高是1尺(1尺=10寸),两扇门的间隙 为2寸,则门槛 为 寸.
三、解答题
14.如图,两艘海舰在海上进行为时2小时的军事演习,一海舰以120海里/时的速度从港口A出发,向北偏东60°方向航行到达B,另一海舰以90海里/时的速度同时从港口A出发,向南偏东30°方向航行到达C,则此时两艘海舰相距多少海里?
15.如图所示,为一棵大树,在树上距地面的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处向上爬到树顶A处,利用拉在A处的滑绳,滑到C处,另一只猴子从D处滑到地面B处,再由B处跑到C处.已知两只猴子所经过的路程都是,求树高的距离.
16.在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
17.如图,学校要把宣传标语掛到教学楼的顶部D处.已知楼顶D处离地面的距离DA为8m,云梯的长度为9m,为保证安全,梯子的底部和墙基的距离AB至少为3m,云梯的顶部能到达D处吗?为什么?
18.拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,拖拉机周围130m以内为受噪声影响区域.
(1)学校C会受噪声影响吗?为什么?
(2)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
19.某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线 ,点A、B分别在 、 上,斜坡AB的长为18米,过点B作 于点C,且线段AC的长为 米.
(1)求该斜坡的坡高BC;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚 为60°,过点M作 于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
一、单选题
1.已知一直角三角形的木板,三边的平方和为1800cm2,则斜边长为( )
A.30cm B.80cm C.90cm D.120cm
2.一根旗杆在离地面3米处断裂,旗杆顶部落在离旗杆底部4米处,旗杆折断之前的高度是( )
A.5米 B.7米 C.8米 D.9米
3.如图,斜面AC的坡比CD:AD=1:2.AC=3 m,坡有一旗杆BC.旗杆顶端B点与A点有一条绝缘钢端相连,若AB=10m.则旗杆BC的高度( )
A.5m B.6m C.8m D.(3+ )m
4.如图所示,某人到岛上去探宝,从A处登陆后先往北走9km,又往东走6km,再折回向北走3km,往西一拐,仅走1km就找到宝藏 问登陆点A与宝藏埋藏点B之间的距离是 .
A.10 B.11 C.12 D.13
5.如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中的线段走,那么从A点到B点的最短距离的走法共有( )
A.1种 B.2种 C.3种 D.4种
6.如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
7.如图,长方形门框高为2m,宽为1.5m,现有3块木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.6m.能从这扇门通过的木板是( )
A.① B.② C.③号 D.都不能通过
8.如图,一根长4 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′,若AA′=2,则BB′的长为( )
A.4 ﹣2 B.4﹣2 C.4 ﹣4 D.2
二、填空题
9.一场暴雨过后,垂直于地面的一棵大树在距地面1m处折断,树尖恰好碰到地面,距树的底部2m,则这棵树高 .
10.如图,两个滑块M,N由一个连杆连接,分别可以在两条互相垂直的滑道上滑动.开始时,滑块M距O点20cm,滑块N距O点15cm,则当滑块M向下滑到O点时,滑块N滑动了
11.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线,交于点O.若,,则 .
12.有一辆装满货物的卡车,宽2.4米(货物的顶部是水平的),要通过如图所示的截面的上半部分是半圆,下半部分长方形的单向道,已知半圆的直径为4米,长方形竖直的一条边长是2.5米,则卡车的外形高必须低于 米.
13.《勾股》中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合2寸,问门广几何?”意思是:如图推开两扇门( 和 ),门边沿D,C两点到门槛 的距高是1尺(1尺=10寸),两扇门的间隙 为2寸,则门槛 为 寸.
三、解答题
14.如图,两艘海舰在海上进行为时2小时的军事演习,一海舰以120海里/时的速度从港口A出发,向北偏东60°方向航行到达B,另一海舰以90海里/时的速度同时从港口A出发,向南偏东30°方向航行到达C,则此时两艘海舰相距多少海里?
15.如图所示,为一棵大树,在树上距地面的D处有两只猴子,它们同时发现地面上的C处有一筐水果,一只猴子从D处向上爬到树顶A处,利用拉在A处的滑绳,滑到C处,另一只猴子从D处滑到地面B处,再由B处跑到C处.已知两只猴子所经过的路程都是,求树高的距离.
16.在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
17.如图,学校要把宣传标语掛到教学楼的顶部D处.已知楼顶D处离地面的距离DA为8m,云梯的长度为9m,为保证安全,梯子的底部和墙基的距离AB至少为3m,云梯的顶部能到达D处吗?为什么?
18.拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,拖拉机周围130m以内为受噪声影响区域.
(1)学校C会受噪声影响吗?为什么?
(2)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
19.某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线 ,点A、B分别在 、 上,斜坡AB的长为18米,过点B作 于点C,且线段AC的长为 米.
(1)求该斜坡的坡高BC;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚 为60°,过点M作 于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
