22.1.4二次函数y=ax? bx c的图象和性质(第一课时) 课件(31张PPT)
文档属性
| 名称 | 22.1.4二次函数y=ax? bx c的图象和性质(第一课时) 课件(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 09:46:29 | ||
图片预览







文档简介
(共31张PPT)
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
第二十二章二次函数
22.1.4二次函数y=ax2+bx+c的图象和性质
(第一课时)
学习目标
1. 通过图象了解二次函数y=ax2+bx+c的性质,体会数形结合的思想.
2.由二次函数y=a(x-h)2+k的图象特征及性质类比地学习二次函数y=ax2+bx+c的图象特征及性质,并能发现它们的联系,培养类比学习能力,渗透数形结合的数学思想方法。
复习提问
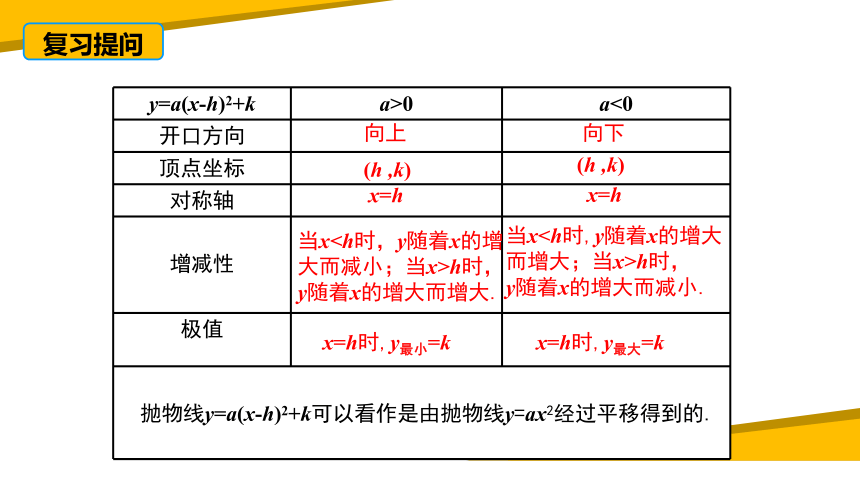
y=a(x-h)2+k a>0 a<0
开口方向
顶点坐标
对称轴
增减性
极值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当xh时,
y随着x的增大而增大.
当xh时,
y随着x的增大而减小.
x=h时,y最小=k
x=h时,y最大=k
抛物线y=a(x-h)2+k可以看作是由抛物线y=ax2经过平移得到的.
探究新知
向右平移6个单位
再向上平移3个单位
探究新知
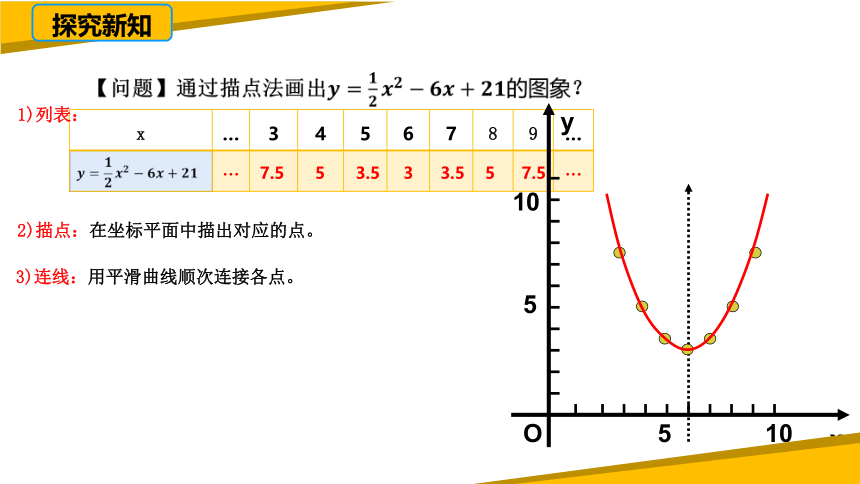
x … 3 4 5 6 7 8 9 …
… …
7.5
5
3.5
3
3.5
1)列表:
2)描点:在坐标平面中描出对应的点。
3)连线:用平滑曲线顺次连接各点。
5
7.5
5
10
5
10
O
x
y
探究新知
【问题】如何画y=ax2+bx+c的图象?
探究新知
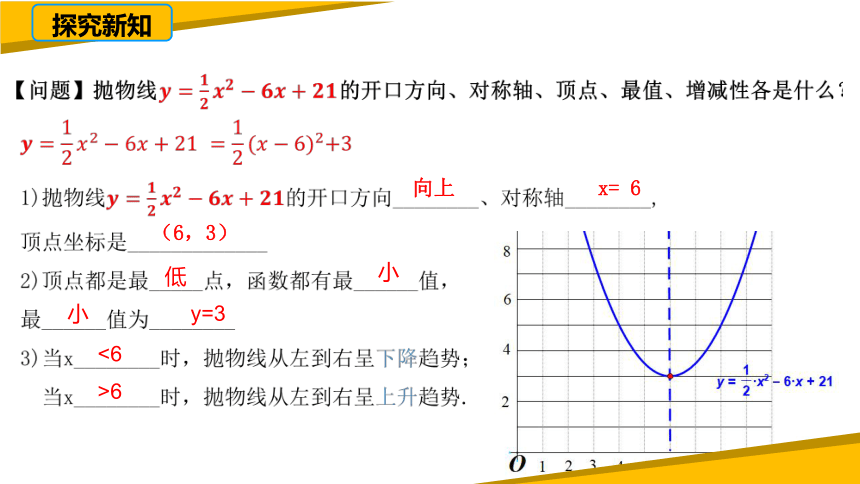
向上
x= 6
(6,3)
小
y=3
低
小
<6
>6
探究新知
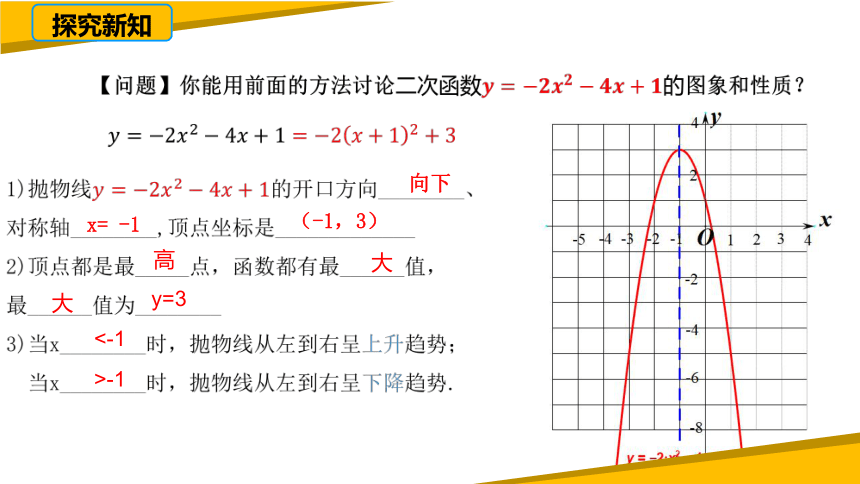
向下
x= -1
(-1,3)
大
y=3
高
大
<-1
>-1
探究新知
探究新知
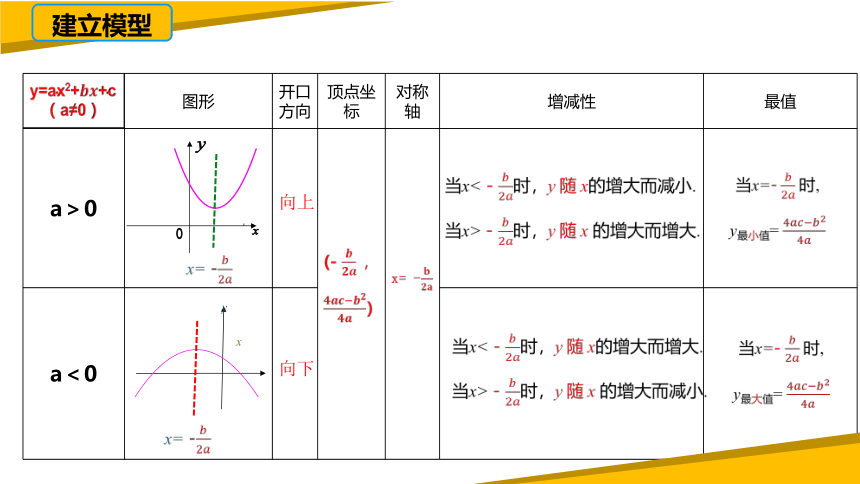
图形 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
x
y
O
y
x
建立模型
典例解析
例1 求出下列抛物线的开口方向,对称轴和顶点坐标.
1)y=2x2-4x+5
2)y=-x2+2x-3
3)y=3x2+2x
4)y=-x2-2x
5)y=-2x2+8x-8
1)开口向上,x = 1,(1, 3)
2)开口向下,x = 1,(1,-2)
4)开口向下,x = -1,(-1,1)
5)开口向下,x = 2,(2,0)
典例解析
典例解析
典例解析
随堂练习
C
随堂练习
D
随堂练习
B
随堂练习
向下
(-2,-1)
直线x=-2
-2
大
-1
随堂练习
中考链接
1.(2023·娄底)已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:
①abc<0;②4a-2b+c>0;③a-b>m(am+b)(m为任意实数)④若点(-3,y1)和点(3,y2)在该图象上,则y1>y2;
其中正确的结论是( )
A.①② B.①④ C.②③ D. ②④
2. (2023·沈阳)二次函数y=-(x+1)2+2图象的顶点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
D
B
中考链接
3. (2023·兰州)已知二次函数y=-3(x-2)2-3,下列说法正确的是( )
A.对称轴为x=-2 B.顶点坐标为(2,3)
C.函数的最大值是-3 D.函数的最小值是-3
C
课堂小结
1.本节课学了哪些主要内容?
2.抛物线y=ax2+bx+c与y=a(x-h)2+k的联系是什么?
3.通过本节课的学习,你想继续探究的知识是什么?
当堂测试
B
C
当堂测试
A
(1,1)
直线x=1
当堂测试
当堂测试
分层作业
B
D
分层作业
1
A
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
第二十二章二次函数
22.1.4二次函数y=ax2+bx+c的图象和性质
(第一课时)
学习目标
1. 通过图象了解二次函数y=ax2+bx+c的性质,体会数形结合的思想.
2.由二次函数y=a(x-h)2+k的图象特征及性质类比地学习二次函数y=ax2+bx+c的图象特征及性质,并能发现它们的联系,培养类比学习能力,渗透数形结合的数学思想方法。
复习提问
y=a(x-h)2+k a>0 a<0
开口方向
顶点坐标
对称轴
增减性
极值
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当x
y随着x的增大而增大.
当x
y随着x的增大而减小.
x=h时,y最小=k
x=h时,y最大=k
抛物线y=a(x-h)2+k可以看作是由抛物线y=ax2经过平移得到的.
探究新知
向右平移6个单位
再向上平移3个单位
探究新知
x … 3 4 5 6 7 8 9 …
… …
7.5
5
3.5
3
3.5
1)列表:
2)描点:在坐标平面中描出对应的点。
3)连线:用平滑曲线顺次连接各点。
5
7.5
5
10
5
10
O
x
y
探究新知
【问题】如何画y=ax2+bx+c的图象?
探究新知
向上
x= 6
(6,3)
小
y=3
低
小
<6
>6
探究新知
向下
x= -1
(-1,3)
大
y=3
高
大
<-1
>-1
探究新知
探究新知
图形 开口方向 顶点坐标 对称轴 增减性 最值
a>0
a<0
向上
向下
x
y
O
y
x
建立模型
典例解析
例1 求出下列抛物线的开口方向,对称轴和顶点坐标.
1)y=2x2-4x+5
2)y=-x2+2x-3
3)y=3x2+2x
4)y=-x2-2x
5)y=-2x2+8x-8
1)开口向上,x = 1,(1, 3)
2)开口向下,x = 1,(1,-2)
4)开口向下,x = -1,(-1,1)
5)开口向下,x = 2,(2,0)
典例解析
典例解析
典例解析
随堂练习
C
随堂练习
D
随堂练习
B
随堂练习
向下
(-2,-1)
直线x=-2
-2
大
-1
随堂练习
中考链接
1.(2023·娄底)已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:
①abc<0;②4a-2b+c>0;③a-b>m(am+b)(m为任意实数)④若点(-3,y1)和点(3,y2)在该图象上,则y1>y2;
其中正确的结论是( )
A.①② B.①④ C.②③ D. ②④
2. (2023·沈阳)二次函数y=-(x+1)2+2图象的顶点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
D
B
中考链接
3. (2023·兰州)已知二次函数y=-3(x-2)2-3,下列说法正确的是( )
A.对称轴为x=-2 B.顶点坐标为(2,3)
C.函数的最大值是-3 D.函数的最小值是-3
C
课堂小结
1.本节课学了哪些主要内容?
2.抛物线y=ax2+bx+c与y=a(x-h)2+k的联系是什么?
3.通过本节课的学习,你想继续探究的知识是什么?
当堂测试
B
C
当堂测试
A
(1,1)
直线x=1
当堂测试
当堂测试
分层作业
B
D
分层作业
1
A
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
